11.2: Valor futuro de las anualidades
- Page ID
- 110897
Aunque es probable que tu jubilación aún esté muy lejos, cuanto antes empieces a invertir más podrás aprovechar el poder de capitalizar los intereses para generar tus ahorros.
¿Te sobresaltó enterarte en la Sección 10.5 que tus ingresos brutos anuales de jubilación podrían necesitar ser de $160,000 cuando cumplas 65 años? ¿Cuánto tiempo vivirás? La esperanza de vida promedio canadiense es de alrededor de 80 años; si vives para tener esa edad, necesitarás 15 años de ingresos de jubilación. Usando una tasa de interés conservadora de 5% compuesta anualmente junto con 3% de inflación anual, esto funciona para ahorrar aproximadamente $2 millones para cuando se jubile. Un objetivo desalentador, ¿no? Bien podría preguntarse: “Si hoy empiezo a ahorrar 300 dólares mensuales, ¿tendré suficiente?”
Claramente es importante saber cuánto valen sus anualidades en el futuro. Esto importa no sólo para las inversiones sino también para las deudas, ya que la mayoría de las empresas y particulares pagan sus deudas a través de estructuras de anualidades. Después de haber realizado varios pagos de anualidades, ¿puede decir en cualquier momento cuánto adeuda usted o su empresa aún por una deuda pendiente?
En la sección anterior aprendiste a reconocer las características fundamentales de las anualidades, por lo que ahora puedes empezar a resolver cualquier anualidad para cualquier variable desconocida. Hay cuatro fórmulas de anualidades. Esta sección abarca los dos primeros, que calculan los valores futuros tanto para las anualidades ordinarias como para las anualidades adeudadas. Estas fórmulas se adaptan tanto a anualidades simples como generales.
Anualidades Ordinarias
El valor futuro de cualquier anualidad es igual a la suma de todos los valores futuros para todos los pagos de anualidad cuando se mueven al final del último intervalo de pago. Por ejemplo, suponga que hará contribuciones de $1,000 al final de cada año durante los próximos tres años a una inversión que gana 10% compuesta anualmente. Se trata de una anualidad simple ordinaria ya que los pagos están al final de los intervalos, y las frecuencias de capitalización y pago son las mismas. Si quisieras saber cuánto dinero tienes en tu inversión después de los tres años, la siguiente figura ilustra cómo aplicarías el concepto fundamental del valor temporal del dinero para mover cada monto de pago a la fecha futura (la fecha focal) y sumar los valores para llegar al valor futuro.

Si bien podría usar esta técnica para resolver todas las situaciones de anualidades, los cálculos se vuelven cada vez más engorrosos a medida que aumenta el número de pagos. En el ejemplo anterior, ¿y si la persona en su lugar hizo contribuciones trimestrales de 250 dólares? Es decir, 12 pagos a lo largo de tres años, lo que resulta en 11 cálculos de valor futuro separados. O si realizaban pagos mensuales, ¡los 36 pagos a lo largo de tres años resultarían en 35 cálculos de valor futuro separados! Claramente, resolver esto sería tedioso y consumiría tiempo, sin mencionar propenso al error. ¡Debe haber una mejor manera!
La Fórmula
La fórmula para el valor futuro de una anualidad ordinaria es de hecho más fácil y rápida que realizar una serie de cálculos de valor futuro para cada uno de los pagos. A primera vista, sin embargo, la fórmula es bastante compleja, por lo que las diversas partes de la fórmula se exploran primero con cierto detalle antes de juntarlas todas.
La fórmula de anualidad es una versión más compleja de la fórmula de tasa, porción y base introducida en el Capítulo 2. Relacionando la Fórmula 2.2 y el primer pago de la cifra anterior da lo siguiente:
\[\begin{array}{l}{\text { Portion }=\text { Base } \times \text { Rate }} \\ {\$ 1,210=\$ 1,000 \times(1+0.1)^{2}}\end{array} \nonumber \]
La porción equivale al valor futuro y la base es igual al monto del pago de anualidad. La tasa se expresa como una fórmula y se escribe como\((1 + 0.1)^2\). No obstante, observe que cada pago en la cifra tiene un exponente diferente para reflejar la capitalización requerida. Esto requiere una adaptación matemática de\((1 + i)^N\), lo que permite determinar una tasa equivalente que represente todos los pagos en un solo cálculo.
Esta tasa equivalente resulta ser una expresión bastante compleja, que se examina en tres partes: el cambio porcentual general, el cambio porcentual con cada pago, y su cociente.
- Numerador - El Porcentaje de Cambio General:\(\left[(1+i)^{\frac{CY}{PY}}\right]^{N}-1\). Esta parte de la fórmula determina el cambio porcentual desde el inicio de la anualidad hasta el final de la anualidad. Tiene tres elementos críticos:
- Conversión de Tasa de Interés\((1+i)^{\frac{CY}{PY}}\). Se debe conocer la tasa de interés que se produce con cada pago. Todos los cálculos de anualidades requieren que el período compuesto sea igual al intervalo de pago. Si esto no es ya el caso, entonces debes convertir la tasa de interés expresada en una tasa de interés equivalente.
- Para anualidades simples, no es necesaria ninguna conversión ya que las frecuencias son las mismas:\(CY = PY\). El exponente de\(\dfrac{CY}{PY}\) siempre es igual a 1 y no tiene ningún efecto.
- Para anualidades generales, recuerde la Fórmula 9.4 para calcular las tasas de interés equivalentes. Aquí la antigua frecuencia de composición forma el numerador (\(CY_{Old}\)) y la nueva frecuencia de composición (que coincide con la frecuencia de pago) forma el denominador (\(CY_{New}) = PY\). Así\(\dfrac{CY_{OLD}}{PY_{New}}\) se convierte\(\dfrac{CY}{PY}\).
- El Compounding\(N\). El exponente compone\(N\) la tasa de interés periódica (que coincide con el intervalo de pago) de acuerdo con el número de pagos de anualidad realizados. Por ejemplo, supongamos que hay dos pagos de fin de año al 10% compuesto semestralmente. Si la tasa de interés se deja semestralmente, hay cuatro compuestos a lo largo de los dos años, lo que no coincide con los pagos. La tasa de interés se convierte dentro de los paréntesis del 10% compuesto semestral a su equivalente a la tasa compuesta anual de 10.25%. El resultado final es que los intereses ahora se compondrán dos veces a lo largo de los dos años, igualando el número de pagos.
- Extracción del punto de partida (−1). Ya que agregaste 1 para realizar la composición, matemáticamente ahora necesitas eliminar el 1. El resultado final es que ahora sabes (en formato decimal) cuánto mayor es el valor futuro en relación con su valor inicial.
- Conversión de Tasa de Interés\((1+i)^{\frac{CY}{PY}}\). Se debe conocer la tasa de interés que se produce con cada pago. Todos los cálculos de anualidades requieren que el período compuesto sea igual al intervalo de pago. Si esto no es ya el caso, entonces debes convertir la tasa de interés expresada en una tasa de interés equivalente.
- Denominador - El Porcentaje de Cambio con Cada Pago:\((1+i)^{\frac{CY}{PY}}-1\). El denominador en la fórmula muestra el cambio porcentual en la cuenta con cada pago realizado. También asegura que el denominador tenga una tasa periódica coincidente con el intervalo de pago.
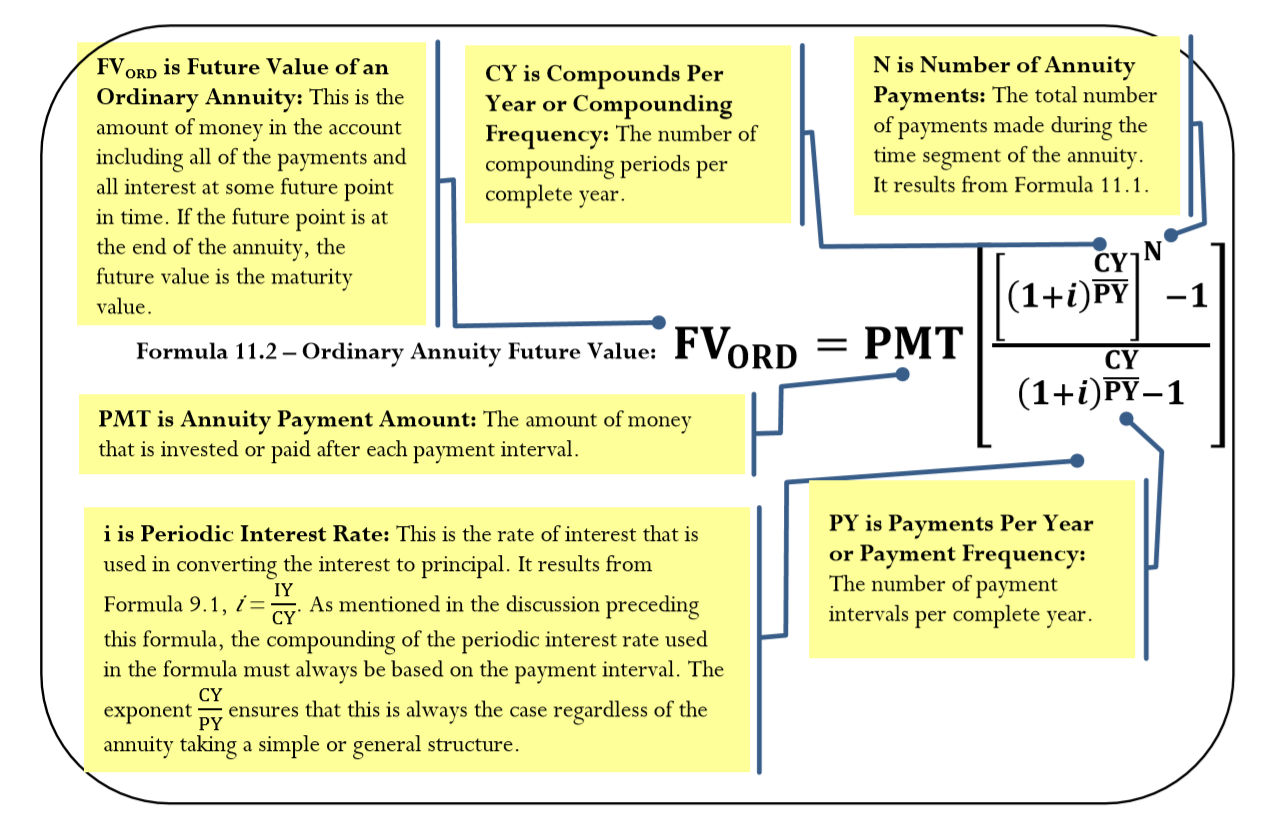
- El Cociente: Al tomar el numerador y dividirlo por el denominador, el cambio porcentual en general se divide por el cambio porcentual con cada pago. Esto establece una relación entre lo que está sucediendo en general en la anualidad versus lo que está sucediendo con cada transacción. Así, este cálculo determina cuánto mayor es el valor final en relación con lo que sucede con cada pago. Esta relación (la tasa) se multiplica luego contra el pago de anualidad (la base) para obtener el saldo final (la porción). Ahora estás en condiciones de ver toda la fórmula mediante la cual calculas el valor futuro de cualquier anualidad ordinaria. Esta fórmula única se aplica independientemente del número de pagos que se realicen. La fórmula 11.2 resume las variables y cálculos requeridos.
Cómo funciona
Hay un proceso de cinco pasos para calcular el valor futuro de cualquier anualidad ordinaria:
Paso 1: Identificar el tipo de anualidad. Dibuja una línea de tiempo para visualizar la pregunta.
Paso 2: Identificar las variables conocidas, incluyendo\(PV, IY, CY, PMT, PY\), y Años.
Paso 3: Usa la Fórmula 9.1 para calcular\(i\).
Paso 4: Si\(PV\) = $0, continúe con el paso 5. Si hay un valor distinto de cero para\(PV\), trátelo como un solo pago. Aplicar la Fórmula 9.2 para determinar\(N\) ya que no se trata de un cálculo de anualidad. Mueva el valor presente al final del segmento de tiempo usando la Fórmula 9.3.
Paso 5: Usa la Fórmula 11.1 para calcular N para la anualidad. Aplicar la Fórmula 11.2 para calcular el valor futuro. Si calculaste un valor futuro en el paso 4, combina los valores futuros de los pasos 4 y 5 para llegar al valor futuro total.
Revisando el escenario de RRSP desde el inicio de esta sección, suponga que tiene 20 años e invierte $300 al final de cada mes durante los próximos 45 años. No has iniciado un RRSP previamente y no tienes saldo de apertura. Es posible una tasa de interés fija del 9% compuesto mensual en el RRSP.
Paso 1: Se trata de una anualidad ordinaria simple ya que las frecuencias coinciden y los pagos están al final del intervalo de pago.

Paso 2: Las variables conocidas son\(PV\) = $0,\(IY\) = 9%,\(CY\) = 12,\(PMT\) = $300,\(PY\) = 12, y Años = 45.
Paso 3: La tasa de interés periódica es\(i\) = 9% ÷ 12 = 0.75%.
Paso 4: Desde\(PV\) = $0, omita este paso.
Paso 5: El número de paym ents es\(N\) = 12 × 45 = 540. La aplicación de la Fórmula 11.2 da lo siguiente:
\[FV_{ORD}=\$ 300\left[\dfrac{\left[(1+0.0075)^{\frac{12}{12}}\right]^{540}-1}{(1+0.0075)^{\frac{12}{12}}-1}\right]=\$ 2,221,463.54 \nonumber \]
De ahí que 540 pagos de $300 al 9% compuesto mensual da como resultado un ahorro total de $2,221,463.54 a la edad de jubilación.
Notas Importantes
Cálculo del Importe de Intereses. Para anualidades de inversión, si te interesa saber cuánto del valor futuro es principal y cuánto es el interés, puedes adaptar la Fórmula 8.3, donde\(I = S – P = FV – PV\).
- El\(FV\) es la solución a la Fórmula 11.2.
- El\(PV\) es el principal (contribuciones totales) calculado tomando\(N × PMT + PV\). En la cifra anterior,\(N × PMT + PV\) = 540 pagos × $300 + $0 = $162,000 en principal. Por lo tanto,\(I\) =$2,221,463.54 − $162,000 = $2,059.463.54, que son los intereses devengados.
Tu Calculadora BAII+. Adaptar sus habilidades de calculadora para adaptarse a las anualidades requiere tres cambios importantes:
- Y ou ahora tiene un valor para PMT. Asegúrese de ingresarlo con la convención de señal de flujo de efectivo correcta. Cuando inviertes, el pago tiene el mismo signo que el\(PV\). Cuando pides prestado, la señal del pago es opuesta a la de\(PV\).
- T l P/Y ya no se establece automáticamente en el mismo valor que C/Y Ingresa tus valores para P/Y y C/Y por separado. Si los valores son los mismos, como en el caso de las anualidades simples, entonces aprovechando la función “Copiar” de tu calculadora te permite evitar tener que clavar el valor en dos veces.
- Si se trata de un valor presente (\(PV\)), por fórmula es necesario hacer dos cálculos usando la Fórmula 9.3 y la Fórmula 11.2. Si ingresa valores para ambos\(PV\) y\(PMT\), la calculadora realiza estos cálculos simultáneamente, requiriendo solo una secuencia para resolver.
Cosas a tener en cuenta
En muchas situaciones de anualidad puede parecer que hay más de una variable desconocida. Por lo general, las variables extra desconocidas son variables “no declaradas” que pueden asumirse razonablemente. Por ejemplo, en la ilustración de RRSP anterior, se podría omitir la declaración “no ha iniciado un RRSP previamente y no tiene saldo de apertura”. Si ya se guardó algo, habría que indicar el número. Como otro ejemplo, es normal terminar un préstamo con saldo cero. Por lo tanto, en una situación de préstamo se puede asumir con seguridad que el valor futuro es cero a menos que se indique lo contrario.
Caminos hacia el éxito
La capacidad de reconocer una anualidad simple puede permitirle simplificar la Fórmula 11.2. Desde CY = PY, estas dos variables forman un cociente de 1 para el exponente. Para una anualidad simple, puede simplificar cualquier aparición de las siguientes expresiones algebraicas en cualquier fórmula de anualidad (no solo Fórmula 11.2) de la siguiente manera:
\((1+i)^{\frac{CY}{PY}}\)en el numerador se puede simplificar a\(1+i\)
y
\((1+i)^{\frac{CY}{PY}}-1\)en el denominador se puede simplificar a solo\(i\)
Por lo tanto, solo para anualidades simples, simplifica la Fórmula 11.2 como\[FV_{ORD}=PMT\left[\dfrac{(1+i)^{N}-1}{i}\right] \nonumber \]
Supongamos que había planeado hacer 10 pagos de anualidades a una inversión. Sin embargo, antes de comenzar a pagar a la inversión, cambiaste de opinión, duplicando tu monto de pago original sin dejar de hacer 10 pagos. ¿Qué sucede con el valor de vencimiento de tu nueva inversión en comparación con el de tu plan original? ¿Tu nuevo saldo será exactamente el doble, más del doble o menos del doble? Explique y justifique su respuesta.
- Contestar
-
Tu nuevo saldo será exactamente el doble. Matemáticamente, has tomado PMT en la Fórmula 11.2 y lo has multiplicado por 2. Esa es la única diferencia entre tu plan original y tu nuevo plan. Por lo tanto, el valor futuro también se duplicará.
Un asesor financiero está revisando una de las cuentas de su cliente. El cliente ha estado invirtiendo $1,000 al final de cada trimestre durante los últimos 11 años en un fondo que ha promediado 7.3% compuesto trimestralmente. ¿Cuánto dinero tiene el cliente hoy en su cuenta?
Solución
Paso 1:
Los pagos se realizan al final de los intervalos de pago, y tanto el periodo compuesto como los intervalos de pago son los mismos. Se trata de una anualidad simple ordinaria. Calcular su valor al final, que es su valor futuro, o\(FV_{ORD}\).
Lo que ya sabes
Paso 1 (continuación):
La línea de tiempo muestra la cuenta del cliente.

Paso 2:
\(PV\)= $0,\(IY\) = 7.3%,\(CY\) = 4,\(PMT\) = $1,000,\(PY\) = 4, Años = 11
Cómo Llegará
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Omita este paso ya que\(PV\) = $0.
Paso 5:
Aplicar Fórmula 11.1 y Fórmula 11.2.
Realizar
Paso 3:
\(i=7.3 \% \div 4=1.825 \%\)
Paso 5:
\(N=4 \times 11=44\)pagos
\[FV_{ORD}=\$ 1000\left[\dfrac{\left[(1+0.01825)^{\frac{4}{4}}\right]^{44}-1}{(1+0.01825)^{\frac{4}{4}}-1}\right]=\$ 66,637.03 \nonumber \]
Instrucciones de la calculadora
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 44 | 7.3 | 0 | -1000 | Respuesta: 66,637.03449 | 4 | 4 |
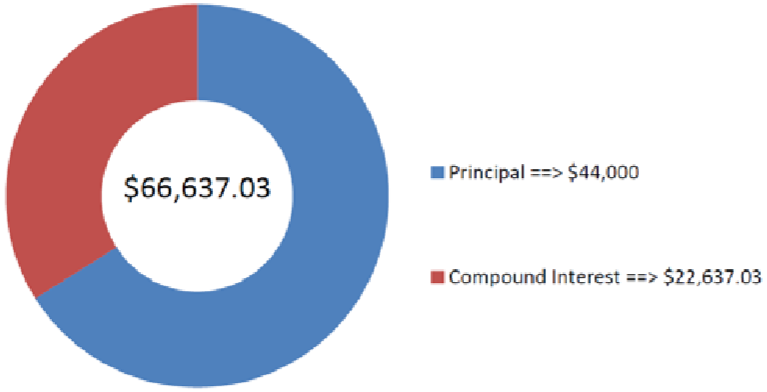
La cifra muestra cuánto capital e interés conforman el saldo final. Después de 11 años de $1,000 contribuciones trimestrales, el cliente tiene $66,637.03 en la cuenta.
Una anualidad de ahorro ya contiene 10,000 dólares. Si se invierten 250 dólares adicionales al final de cada mes al 9% compuesto semestralmente por un plazo de 20 años, ¿cuál será el valor de vencimiento de la inversión?
Solución
Paso 1:
Los pagos se realizan al final de los intervalos de pago, y el período compuesto y los intervalos de pago son diferentes. Se trata de una anualidad general ordinaria. Calcular su valor al final, que es su valor futuro, o\(FV_{ORD}\).
Lo que ya sabes
Paso 1 (continuación):
La línea de tiempo aparece a continuación.

Paso 2:
\(PV\)= $10,000,\(IY\) = 9%,\(CY\) = 2,\(PMT\) = $250,\(PY\) = 12, Años = 20
Cómo Llegará
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Aplica la Fórmula 9.2 y la Fórmula 9.3.
Paso 5:
Aplicar Fórmula 11.1 y Fórmula 11.2 El valor final futuro es la suma de las respuestas al paso 4 (\(FV\)) y al paso 5 (\(FV_{ORD}\)).
Paso 3:
\(i=9 \% \div 2=4.5 \%\)
Paso 4:
\(N=2 \times 20=40\)compuestos
\[FV=\$ 10,000(1+0.045)^{40}=\$ 58,163.64538 \nonumber \]
Paso 5:
\(N=12 \times 20=240\)pagos
\[FV_{ORD }=\$ 250\left[\dfrac{\left[(1+0.045)^{\frac{2}{12}}\right]^{240}-1}{(1+0.045)^{\frac{2}{12}}-1}\right]=\$ 163,529.9492 \nonumber \]
\[\text {Total }FV=\$ 58,163.64538+\$ 163,529.9492=\$ 221,693.59 \nonumber \]
Instrucciones de la calculadora
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 240 | 9 | -10000 | -250 | Respuesta: 221,693,5946 | 12 | 2 |
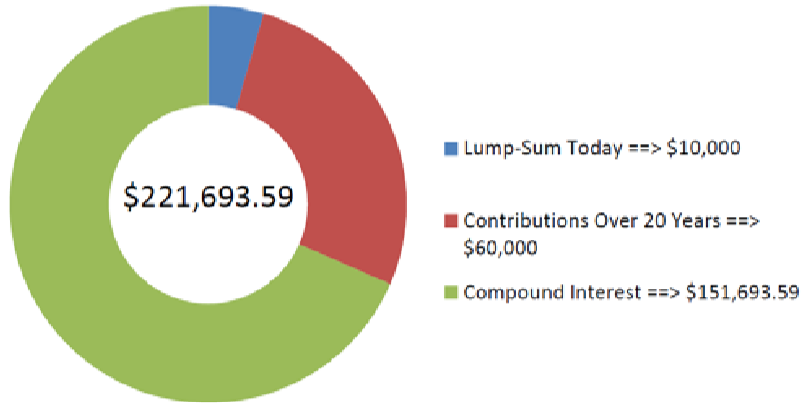
La cifra muestra cuánto capital e interés conforman el saldo final. La anualidad de ahorro tendrá un saldo de 221,693.59 dólares después de los 20 años.
Notas Importantes
Si alguna de las variables, incluyendo\(IY, CY, PMT\), o\(PY\), cambio entre el punto inicial y final de la anualidad, o si se realiza algún depósito o retiro de pago único adicional, se crea un nuevo segmento de tiempo que debe tratarse por separado. Luego habrá varios segmentos de tiempo que requieren que trabajes de izquierda a derecha repitiendo los pasos del 3 al 5 en el procedimiento. El valor futuro al final de un segmento de tiempo se convierte en el valor presente en el siguiente segmento de tiempo. Ejemplo\(\PageIndex{3}\) ilustra este concepto.
Cosas a tener en cuenta
Preste especial atención cuando la variable que cambia entre segmentos de tiempo es la frecuencia de pago (\(PY\)). Cuando se introduce en una calculadora BAII+, la copia\(PY\) automáticamente a través de la frecuencia de composición (\(CY\)). A menos que\(CY\) también hayas cambiado a la misma frecuencia, esto significa que debes desplazarte hacia abajo hasta la ventana CY y volver a ingresar el valor correcto para esta variable, incluso si no cambió.
Caminos hacia el éxito
Al trabajar con múltiples segmentos de tiempo, es importante que siempre comiences tus cálculos en el lado opuesto a la variable desconocida. Para los cálculos de valores futuros, esto significa que comienzas en el lado izquierdo de tu línea de tiempo; para los cálculos del valor actual, comienza en el lado derecho.
Genevieve ha decidido comenzar a ahorrar para unas vacaciones en dos años, cuando se gradúa de la universidad. Ella ya tiene mil mil dólares ahorrados hoy. Para el primer año, planea hacer contribuciones de fin de mes de $300 y luego cambiar a contribuciones de fin de trimestre de $1,000 en el segundo año. Si la cuenta puede ganar 5% compuesto semestral en el primer año y 6% compuesto trimestralmente en el segundo año, ¿cuánto dinero habrá ahorrado cuando se gradúe?
Solución
Paso 1:
Hay un cambio de variables después de un año. Como resultado, necesitas un segmento de tiempo de Año 1 y un segmento de tiempo de Año 2. En ambos segmentos, los pagos se encuentran al final del periodo. En el Año 1, el periodo compuesto y los intervalos de pago son diferentes. En el año 2, el periodo compuesto y los intervalos de pago son los mismos. Se trata de una anualidad general ordinaria seguida de una anualidad simple ordinaria. Tu objetivo es calcular el valor futuro, o\(FV_{ORD}\).
Lo que ya sabes
Paso 1 (continuación):
El cronograma de sus ahorros de vacaciones aparece a continuación.
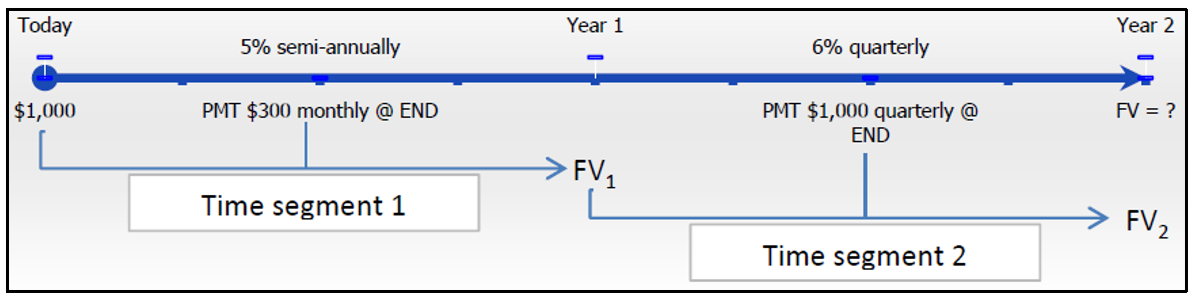
Paso 2:
Segmento de tiempo 1:\(PV\) = $1,000,\(IY\) = 5%,\(CY\) = 2,\(PMT\) = $300,\(PY\) = 12, Años = 1
Segmento\(PV = FV_1\) de tiempo 2: del segmento de tiempo 1,\(IY\) = 6%,\(CY\) = 4,\(PMT\) = $1,000,\(PY\) = 4, Años = 1
Cómo Llegará
Para cada segmento de tiempo, repita los siguientes pasos:
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Aplica la Fórmula 9.2 y la Fórmula 9.3.
Paso 5:
Aplicar Fórmula 11.1 y Fórmula 11.2. El valor futuro total en cualquier segmento de tiempo es la suma de las respuestas al paso 4 (\(FV\)) y al paso 5 (\(FV_{ORD}\)).
Realizar
Para el primer segmento de tiempo:
Paso 3:
\(i=5 \% \div 2=2.5 \%\)
Paso 4:
\(N=2 \times 1=2\)compuestos
\[FV_{1}=\$ 1,000(1+0.025)^{2}=\$ 1,050.625 \nonumber \]
Paso 5:
\(N=12 \times 1=12\)pagos
\[FV_{ORD1}=\$ 300\left[\dfrac{\left[(1+0.025)^{\frac{2}{12}}\right]^{12}-1}{(1+0.025)^{\frac{2}{12}}-1}\right]=\$ 3,682.786451 \nonumber \]
\[\text {Total } FV_{1}=\$ 1,050.625+\$ 3,682.786451=\$ 4,733.411451 \nonumber \]
Para el segundo segmento de tiempo:
Paso 3:
\(i=6 \% \div 4=1.5 \%\)
Paso 4:
\(N=4 \times 1=4\)compuestos
\[FV_{2}=\$ 4,733.411451(1+0.015)^{4}=\$ 5,023.870384 \nonumber \]
Paso 5:
\(N=4 \times 1=4\)pagos
\[FV_{ORD2}=\$ 1,000\left[\dfrac{\left((1+0.015)^{\frac{4}{4}}\right]^{4}-1}{(1+0.015)^{\frac{4}{4}}-1}\right]=\$ 4,090.903375 \nonumber \]
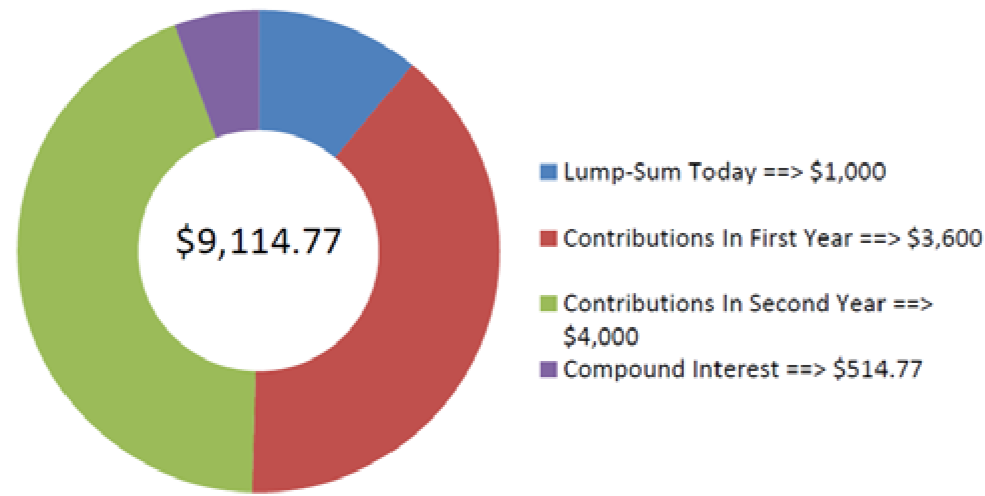
\[\text { Total } FV_{2}=\$ 5,023.870384+\$ 4,090.903375=\$ 9,114.77 \nonumber \]
Instrucciones de la calculadora
| Segmento de tiempo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 12 | 5 | -1000 | -300 | Respuesta: 4,733,411451 | 12 | 2 |
| 2 | 4 | 6 | -4,733.411451 | -1000 | Respuesta: 9,114,773759 | 4 | 4 |
La cifra muestra cuánto capital e interés conforman el saldo final. Cuando Genevieve se gradúe habrá ahorrado $9,114.77 para sus vacaciones.
Anualidades vencidas
Una anualidad adeudada ocurre cuando los pagos se realizan al inicio del intervalo de pago. Para entender la diferencia que esto hace con el valor futuro, recalculemos el ejemplo de RRSP anterior en esta sección, pero tratémoslo como una anualidad adeudada. Desea conocer el valor futuro de hacer contribuciones anuales de $1,000 al inicio de cada intervalo de pago para los próximos tres años a una inversión que gana 10% compuesta anualmente. Esto forma una simple anualidad adeudada. La siguiente figura ilustra cómo se aplica el concepto fundamental del valor temporal del dinero para mover cada monto de pago a la fecha futura (la fecha focal) y sumar los valores para llegar al valor futuro.
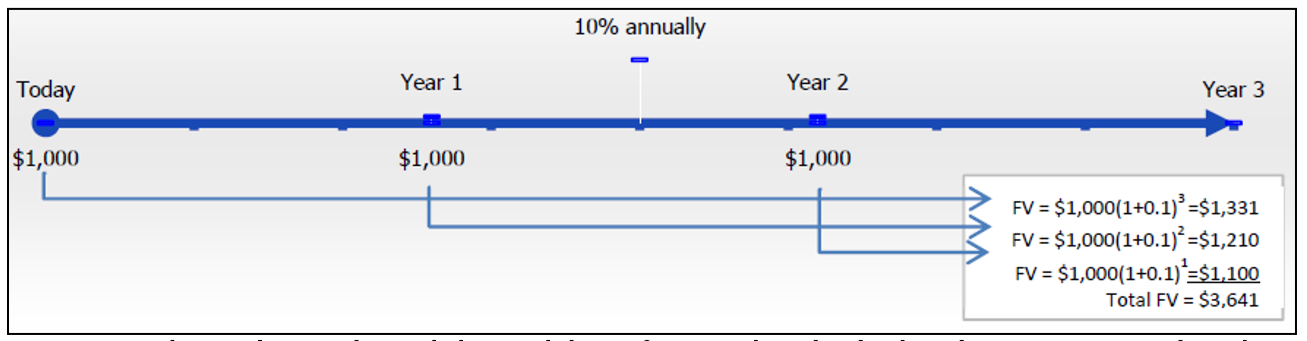
Tenga en cuenta que no termina con el mismo saldo de $3,310 alcanzado bajo la anualidad ordinaria. En cambio, tienes un saldo mayor de $3,641. ¿Por qué es esto? Colocar los dos tipos de anualidades uno al lado del otro en la siguiente figura demuestra la diferencia clave entre los dos ejemplos.
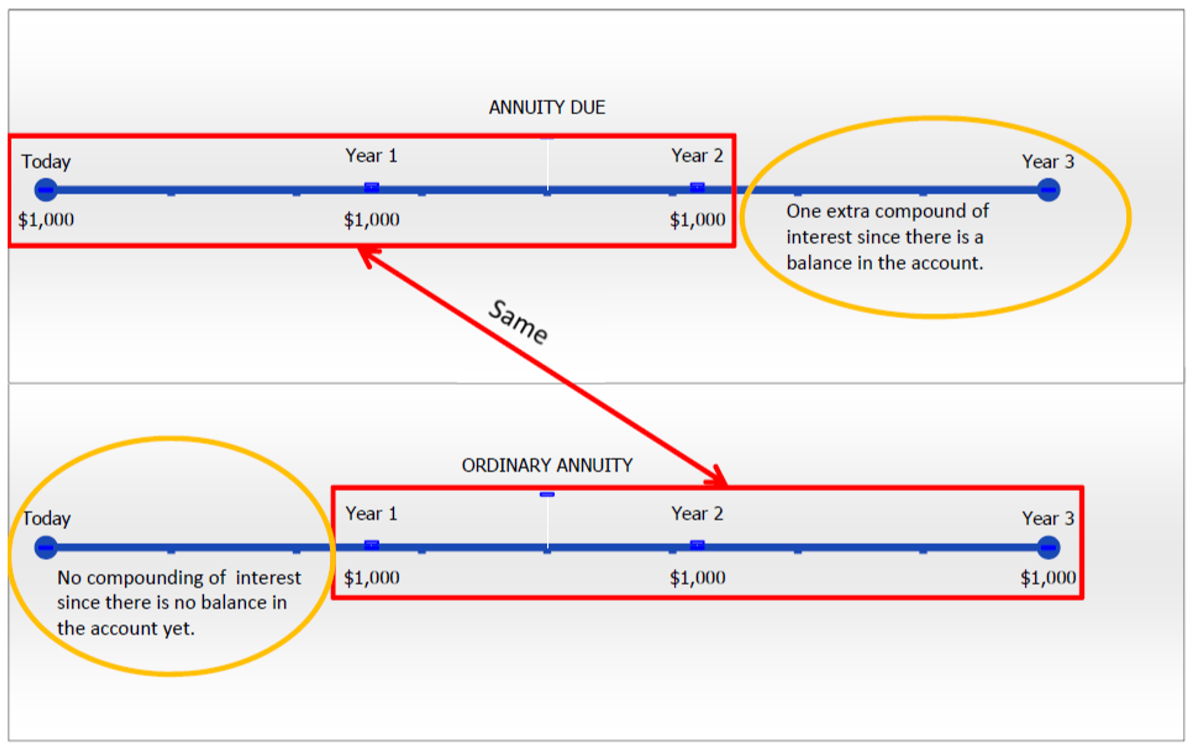
Ambas anualidades tienen una secuencia idéntica de tres pagos de $1,000. No obstante, en la anualidad ordinaria no se devengan intereses durante el primer intervalo de pago ya que el principal es cero y el pago no ocurre hasta el final del intervalo. Por otra parte, en la anualidad adeudada se gana un compuesto extra de intereses en el último intervalo de pago por el principal existente al cierre del segundo año. Si tomas el saldo final de la anualidad ordinaria de $3,310 y le das un compuesto extra tienes\(FV\) = $3,310 (1 + 0.1) = $3,641. En resumen, la diferencia clave entre los dos tipos de anualidades es que una anualidad adeudada siempre recibe un compuesto extra de interés.
La Fórmula
La adaptación de la fórmula de valor futuro de anualidad ordinaria para adaptarse al compuesto adicional crea la Fórmula 11.3. Obsérvese que todas las variables en la fórmula siguen siendo las mismas; sin embargo, se cambia el subíndice en el símbolo FV para reconocer la diferencia en el cálculo requerido.
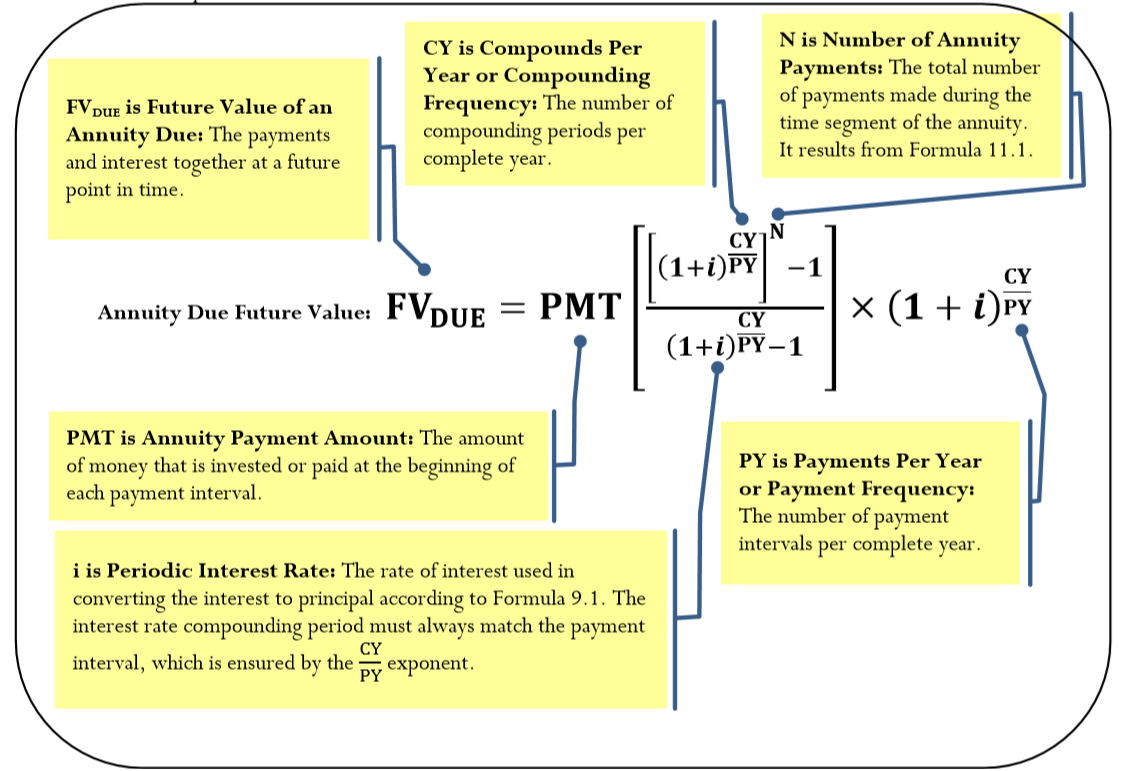
Cómo funciona
Los pasos requeridos para resolver fo r el valor futuro de una anualidad adeudada son casi idénticos a los que utiliza para la anualidad ordinaria. La única diferencia radica en el paso 5, donde se usa la Fórmula 11.3 en lugar de la Fórmula 11.2. Ejemplo\(\PageIndex{4}\) y Ejemplo\(\PageIndex{5}\) ilustran la adaptación.
Notas Importantes

Para adaptar su calculadora a una anualidad vencida, debe alternar la configuración de tiempo de pago de END a BGN. El valor predeterminado de la calculadora es FIN, que es la anualidad ordinaria. El ajuste del tiempo de pago se encuentra en el segundo estante encima de la clave PMT (¡porque está relacionado con el PMT!). Para alternar la configuración, complete la siguiente secuencia:
- 2do BGN (se muestra el tiempo de pago actual de END o BGN)
- 2º SET (cambia a la otra configuración)
- 2º Salir (para salir de la ventana)
Cuando la calculadora está en modo de vencimiento de anualidad, aparece un pequeño BGN en la esquina superior derecha de su calculadora. Para devolver la calculadora al modo ordinario, repita lo anterior
En igualdad de condiciones,
- Para cualquier inversión, que siempre tendrá el mayor valor futuro: ¿una anualidad ordinaria o una anualidad adeudada? Explique.
- Para cualquier deuda, que siempre tendrá un mayor valor futuro: ¿una anualidad ordinaria o una anualidad adeudada? Explique.
- Contestar
-
- La anualidad adeudada tendrá el mayor valor futuro, ya que siempre tiene un compuesto extra en comparación con una anualidad ordinaria.
- La anualidad ordinaria tendrá el mayor valor futuro, ya que el principal en el primer intervalo de pago es mayor y por lo tanto devengan más intereses que en la anualidad adeudada.
El boleto instantáneo de Scratch n' win Set for Life ofrece a los jugadores la oportunidad de ganar $1,000 por semana durante los próximos 25 años comenzando inmediatamente después de la validación. Si un ganador fuera a invertir todo su dinero en una cuenta ganando 5% compuesto anualmente, ¿cuánto dinero tendría al final de su mandato de 25 años? Asumir que cada año tiene exactamente 52 semanas.
Solución
Paso 1:
Los pagos comienzan inmediatamente, y el período compuesto y los intervalos de pago son diferentes. Por lo tanto, esta una anualidad general adeudada. Calcular su valor al final, que es su valor futuro, o\(FV_{DUE}\).
Lo que ya sabes
Paso 1 (continuación):
El cronograma para los ahorros de lotería está a continuación.

Paso 2:
\(PV\)= $0,\(IY\) = 5%,\(CY\) = 1,\(PMT\) = $1,000,\(PY\) = 52, Años = 25
Cómo Llegará
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Sáltate este paso ya que no hay\(PV\).
Paso 5:
Aplicar Fórmula 11.1 y Fórmula 11.3.
Realizar
Paso 3:
\(i=5 \% \div 1=5 \% \)
Paso 5:
\(N=52 \times 25=1,300\)pagos
\[\begin {aligned}FV_{DUE}&=\$ 1,000\left[\dfrac{\left[(1+0.05)^{\frac{1}{52}}\right]^{1300}-1}{(1+0.05)^{\frac{1}{52}}-1} \times(1+0.05)^{\frac{1}{52}}\right]\\&=\$2,544,543.22 \end{aligned} \nonumber \]
Instrucciones de la calculadora
| Modo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 1300 | 5 | 0 | -1000 | Respuesta: 2,544,543,218 | 52 | 1 |
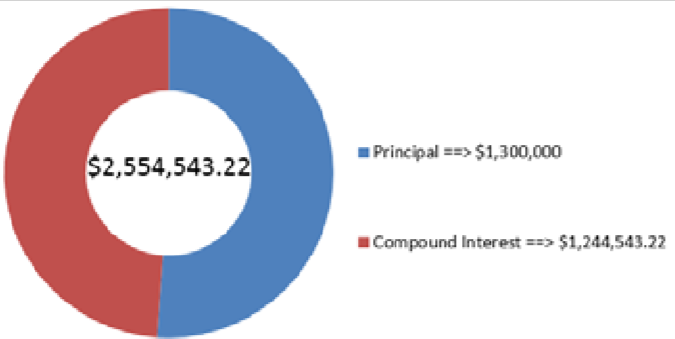
La cifra muestra cuánto capital e interés conforman el saldo final. Si el ganador fuera a invertir todo el dinero de su premio de lotería, tendría 2.544.543.22 dólares después de 25 años.
Cuando nació el hijo de Roberto, Roberto comenzó a realizar pagos de $1,000 al inicio de cada seis meses a un fondo fiduciario que ganaba 5.75% compuesto mensualmente. Después de cinco años, cambió sus contribuciones y comenzó a depositar $500 al inicio de cada trimestre. ¿Cuánto dinero habrá en el fondo fiduciario de su hijo cuando su hijo cumpla 18 años?
Solución
Paso 1:
Hay un cambio de variables después de cinco años. Como resultado, necesitas dos segmentos de tiempo. En ambos segmentos, los pagos son al inicio del periodo y los periodos compuestos y los intervalos de pago son diferentes. Por lo tanto, Roberto tiene dos anualidades generales consecutivas vencidas. Combinado, calcular el valor futuro, o\(FV_{DUE}\).
Lo que ya sabes
Paso 1 (continuación):
El cronograma para el fondo fiduciario se encuentra a continuación.
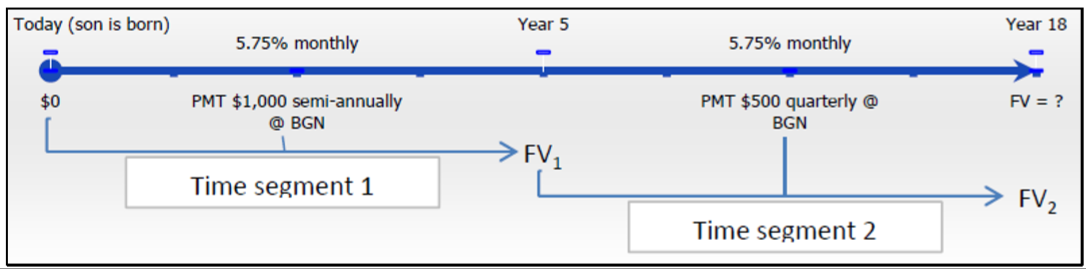
Paso 2:
Segmento de tiempo 1:\(PV\) = $0,\(IY\) = 5.75%,\(CY\) = 12,\(PMT\) = $1,000,\(PY\) = 2, Años = 5
Segmento\(PV = FV_1\) de tiempo 2: del segmento de tiempo 1,\(IY\) = 5.75%,\(CY\) = 12,\(PMT\) = $500,\(PY\) = 4, Años = 13
Cómo Llegará
Para cada segmento de tiempo, repita los siguientes pasos:
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Si hay una\(PV\), aplique la Fórmula 9.2 y la Fórmula 9.3.
Paso 5:
Aplicar Fórmula 11.1 y Fórmula 11.3. El valor futuro total en cualquier segmento de tiempo es la suma de las respuestas al paso 4 (\(FV\)) y al paso 5 (\(FV_{ORD}\)).
Realizar
Paso 3:
\(i=5.75 \% \div 12=0.4719 \overline{6} \%\)
Paso 4:
No\(PV\), así que omita este paso.
Paso 5:
\(N=2 \times 5=10\)pagos
\[FV_{DUE1}=\$ 1,000\left[\dfrac{\left[(1+0.004719 \overline{6})^{\frac{12}{2}}\right]^{10}-1}{(1+0.004719 \overline{6})^{\frac{12}{2}}-1} \times(1+0.004719 \overline{6})^{\frac{12}{2}}\right]=\$ 11,748.47466=FV_1 \nonumber \]
\[\text { Total } FV_{2}=\$ 24,765.17+\$ 38,907.21529=\$ 63,672.39 \nonumber \]
Instrucciones de la calculadora
| Segmento de tiempo | Modo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| 1 | BGN | 10 | 5.75 | 0 | -1000 | Respuesta: 11,748.47466 | 2 | 12 |
| 2 | \(\surd\) | 52 | \(\surd\) | -11,748.47466 | -500 | Respuesta: 63,672.385 .29 | 4 | 12 |
La cifra muestra cuánto capital e interés conforman el saldo final. Cuando el hijo de Roberto cumpla 18 años, el fondo fiduciario tendrá un saldo de 63.672.39 dólares.