11.1: Fundamentos de Anualidades

Última actualización
Guardar como PDF

Page ID: 110889

Jean-Paul Olivier
Red River College of Applied Arts, Science, & Technology

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Es imposible calcular los pagos con precisión hasta que reconozca algunas de las características clave ilustradas en la introducción del capítulo:

Muchos de los ejemplos requerían un pago por la misma cantidad de forma regular, como los 872.41 dólares mensuales para su hipoteca.
El momento de los pagos varió. El arrendamiento de auto requirió el primer pago por adelantado (a principios de mes), mientras que la compra de hipoteca y colchón tuvo el primer pago adeudado un mes después de la compra (al final del mes).
La frecuencia de los pagos y la frecuencia de la tasa de interés variaron. La hipoteca tenía pagos mensuales con intereses que se cobraban semestralmente, mientras que el arrendamiento del auto tenía pagos mensuales e intereses mensuales.

A diferencia de los pagos únicos (cubiertos en el Capítulo 9) para los que solo hay una fórmula, se resuelven series de pagos eligiendo la fórmula apropiada entre cuatro posibilidades definidas por las características financieras de los pagos. Esta sección define las características de cuatro tipos diferentes de series de pagos y luego las contrasta con los cálculos de pago único del Capítulo 9 y del Capítulo 10. En esta sección también se desarrolla una nueva estructura simplificada de cronogramas para ayudarle a visualizar una serie de pagos.

¿Qué son las anualidades?

Una anualidad es un flujo continuo de pagos periódicos iguales de una parte a otra por un período de tiempo específico para cumplir con una obligación financiera. Un pago de anualidad es el monto en dólares del pago periódico igual en un entorno de anualidad. La siguiente figura ilustra una anualidad semestral con pagos mensuales. Observe que los pagos son continuos, iguales, periódicos y ocurren en un período de tiempo fijo. Si alguna de estas cuatro características no se satisface, entonces la transacción financiera no cumple con la definición de una anualidad singular y requiere de otras técnicas y fórmulas para resolver.

$clipboard_e554f8d5c481e045024b7d25b08ae4e8a.png$

Los ejemplos a continuación ilustran cuatro líneas de tiempo que se parecen a la anterior, pero con una de las características de una anualidad violada. Esto significa que ninguno de los siguientes en su totalidad se considera una anualidad:

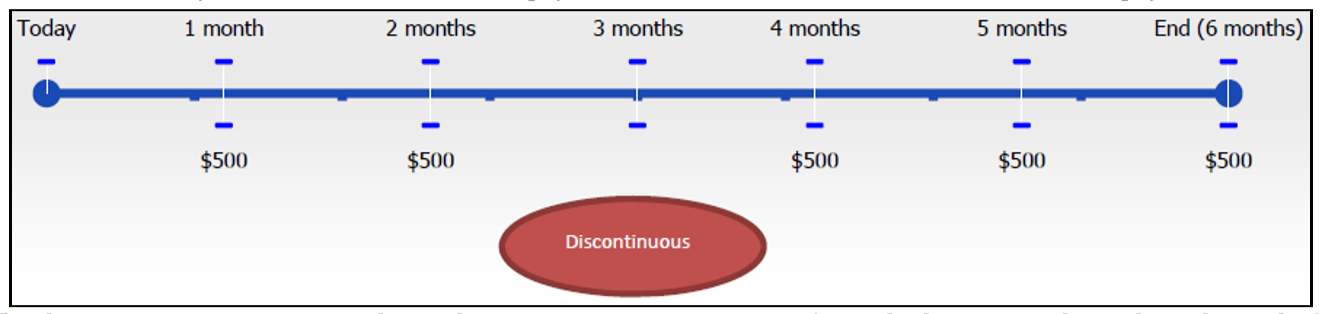
Continuo. Los pagos de anualidades son sin interrupciones ni interrupciones desde el inicio hasta el final del plazo de la anualidad. En la cifra anterior no hay descansos en la anualidad ya que cada mes tiene un pago de anualidad. Esta siguiente cifra no es una anualidad porque la ausencia de un pago en el tercer mes hace que la serie de pagos sea discontinua.

$clipboard_eaf71a2a3b3063170b5eefdf74f06a7e1.png$

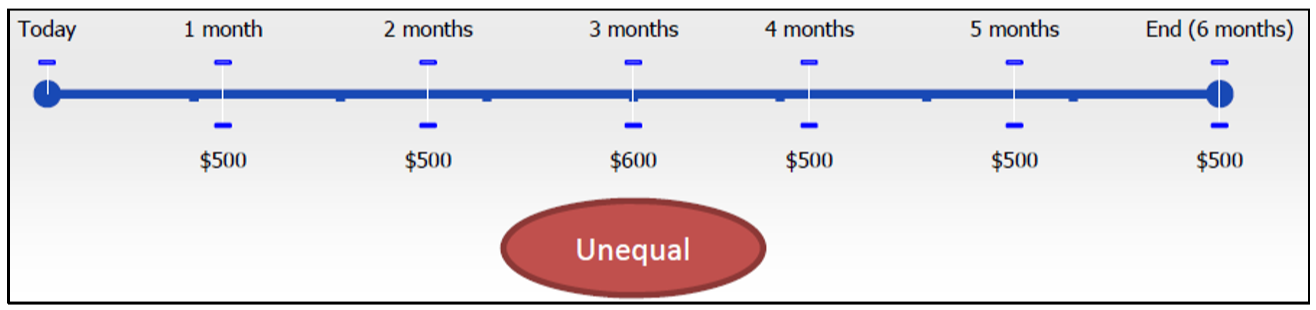
Igual. Los pagos de anualidad deben estar en la misma cantidad cada vez desde el inicio hasta el final del plazo de la anualidad. En la cifra original, cada anualidad mensual es de $500. Observe que en esta siguiente figura el monto del pago varía e incluye valores tanto de $500 como de $600.

$clipboard_ea4de913d6be6d3922284947a8b3c38da.png$

Periódicos. La cantidad de tiempo entre cada pago de anualidad continuo e igual se conoce como intervalo de pago. De ahí que un intervalo de pago mensual significa que los pagos tienen un mes entre ellos, mientras que un intervalo de pago semestral significa que los pagos tienen seis meses entre ellos. Los pagos de anualidades deben tener siempre el mismo intervalo de pago desde el inicio hasta el final del plazo de la anualidad. En la cifra original hay exactamente un mes entre cada pago igual y repetido en la anualidad. Observe que en esta siguiente figura los pagos, aunque iguales y continuos, no ocurren con la misma cantidad de tiempo entre cada uno. De hecho, los tres primeros pagos se realizan mensualmente mientras que los tres últimos pagos se realizan trimestralmente. (Puede notar que si los tres primeros pagos se tratan por separado de los tres últimos pagos, entonces cada agrupación separada representa una anualidad y por lo tanto hay dos anualidades separadas. No obstante, en su conjunto esto no es una anualidad.)

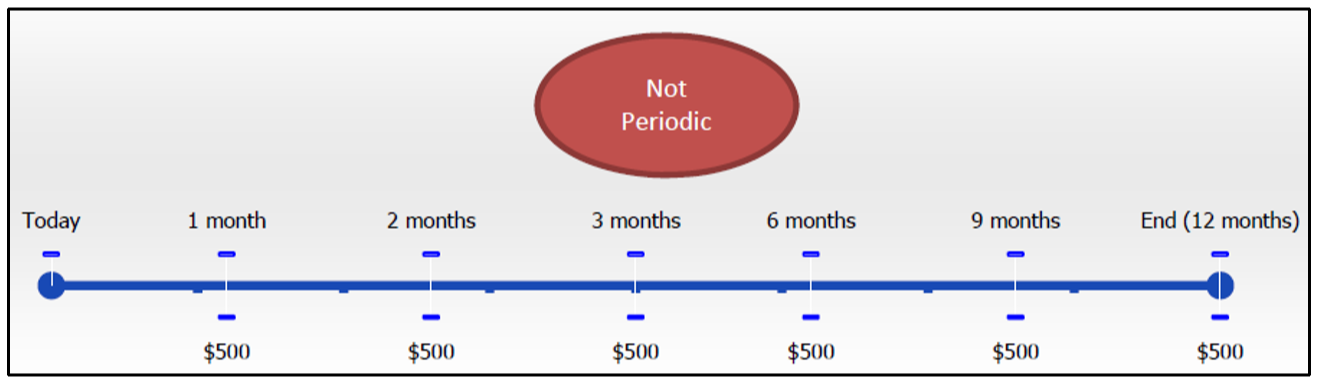
$clipboard_e9f85edae5cabfc59103ffc8fd03f88ef.png$

Periodo de Tiempo Especificado. Los pagos de anualidades deben ocurrir dentro de un marco de tiempo identificable que tenga un comienzo y un final especificados. El marco temporal de la anualidad puede ser (1) conocido con una fecha de inicio definida y una fecha de finalización definida, como la anualidad ilustrada en la figura original, que perdura por seis periodos; (2) conocida pero no concluida, como comenzar hoy y continuar para siempre en el futuro (de ahí un periodo de tiempo infinito); o (3) desconocido pero teniendo un punto de terminación claro, por ejemplo, los pagos mensuales de pensiones que comienzan cuando te jubilas y terminan cuando mueres, una fecha que obviamente no se conoce de antemano. En la siguiente figura, la anualidad no tiene fecha de finalización definida, no continúa en el futuro, y no es identificable ningún punto de terminación claro.

$clipboard_ee238a31868aa3623ab266b02028f4666.png$

En resumen, la primera cifra es una anualidad que se adhiere a las cuatro características y puede abordarse a través de una fórmula de anualidad. Las siguientes cuatro cifras no son anualidades y necesitan otras técnicas o fórmulas financieras para realizar los cálculos necesarios.

Tipos de anualidades

Existen cuatro tipos de anualidades, las cuales se basan en la combinación de dos características clave: el momento de los pagos y la frecuencia. Vamos a explorar estas características primero, después de lo cual discutiremos los diferentes tipos de anualidades.

Momento de Pagos. Un ejemplo ilustra mejor esta característica. Supongamos que hoy mismo consigues un préstamo con pagos mensuales. Si realizaras tu primer pago de anualidad el día que recibas el préstamo, el monto de capital adeudado se reduciría inmediatamente y acumularías una cantidad menor de interés durante tu primer mes. Esto se llama hacer su pago de anualidad al inicio de un intervalo de pago, y este pago se conoce como adeudado. Sin embargo, si pasa un mes antes de realizar su primer pago mensual del préstamo, su principal original acumula más intereses que si el principal ya se hubiera reducido. Esto se llama realizar tu pago al final del intervalo de pago, y este pago se conoce como ordinario porque es la forma más común de pago de anualidad. Dependiendo de cuándo realice su pago, se producen diferentes cantidades de capital e intereses.
Frecuencia. La frecuencia de una anualidad se refiere a una comparación entre la frecuencia de pago y la frecuencia de capitalización. Una frecuencia de pago es el número de pagos de anualidades que se producirían en un año completo. Recordemos del Capítulo 9 que la frecuencia de composición es el número de compuestos por año completo. Si la frecuencia de pago es la misma que la frecuencia de capitalización, esto se denomina anualidad simple. Cuando se cobran intereses a la cuenta mensualmente y los pagos también se realizan mensualmente, se determina el principal y los intereses mediante fórmulas simplificadas. Sin embargo, si la frecuencia de pago y la frecuencia de capitalización son diferentes, esto se denomina anualidad general. Si, por ejemplo, haces pagos mensuales mientras los intereses se componen semestralmente, tienes que usar fórmulas más complejas para determinar el principal y los intereses ya que el pago del principal y el cobro de intereses no ocurren simultáneamente.

Al juntar estas dos características en sus cuatro combinaciones se crean los cuatro tipos de anualidades. Cada cronograma en estas cifras supone una transacción que implica seis pagos semestrales durante un período de tres años.

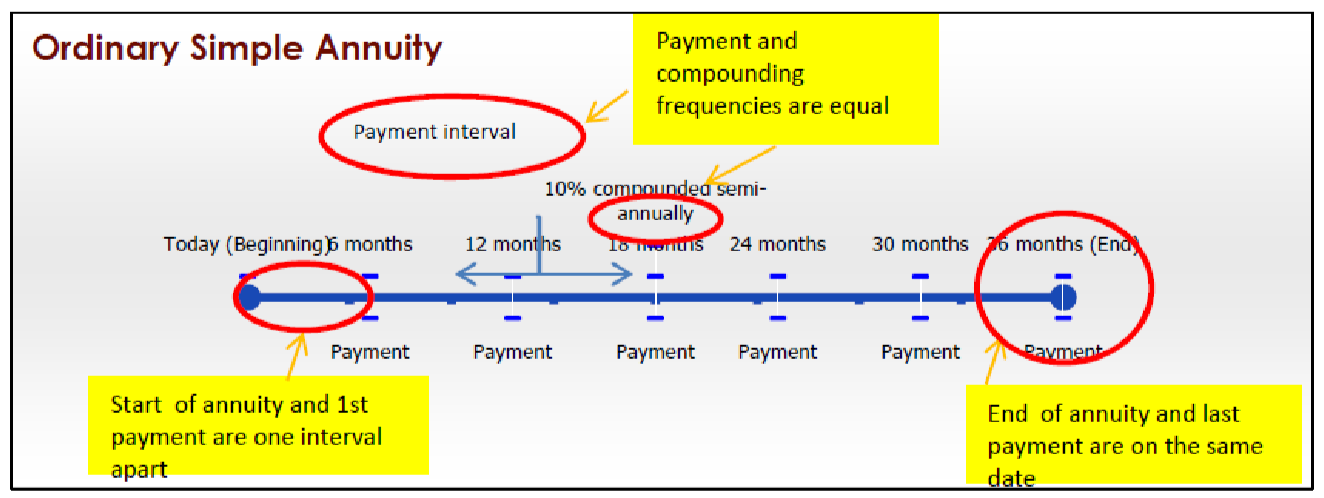
$clipboard_ed515063a3f2494da95647671f5e35dbe.png$

Anualidad Simple Ordinaria

Una anualidad simple ordinaria tiene las siguientes características:

Los pagos se realizan al final de los intervalos de pago, y las frecuencias de pago y capitalización son iguales.
El primer pago ocurre un intervalo después del inicio de la anualidad.
El último pago se produce en la misma fecha que el final de la anualidad.

Por ejemplo, la mayoría de los préstamos para automóviles son anualidades simples ordinarias donde los pagos se realizan mensualmente y las tasas de interés se componen mensualmente. Además, los préstamos para automóviles no requieren el primer pago mensual hasta el final del primer mes.

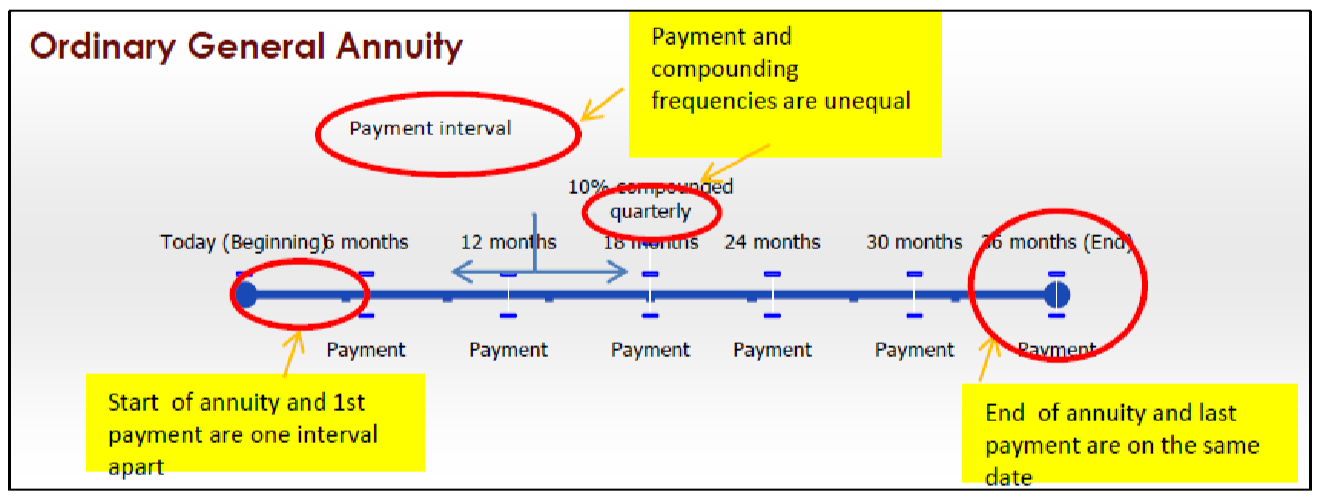
$clipboard_eecdddc770fa7a30e8eb165d3c7e69a7d.png$

Anualidad General Ordinaria

Una anualidad general ordinaria tiene las siguientes características:

Los pagos se realizan al final de los intervalos de pago, y las frecuencias de pago y capitalización son desiguales.
El primer pago ocurre un intervalo después del inicio de la anualidad.
El último pago se produce en la misma fecha que el final de la anualidad.

Por ejemplo, la mayoría de las hipotecas son anualidades generales ordinarias, donde los pagos se realizan mensualmente y las tasas de interés se componen semestralmente. Al igual que con los préstamos para automóviles, no se requiere su primer pago mensual hasta que transcurra un mes.

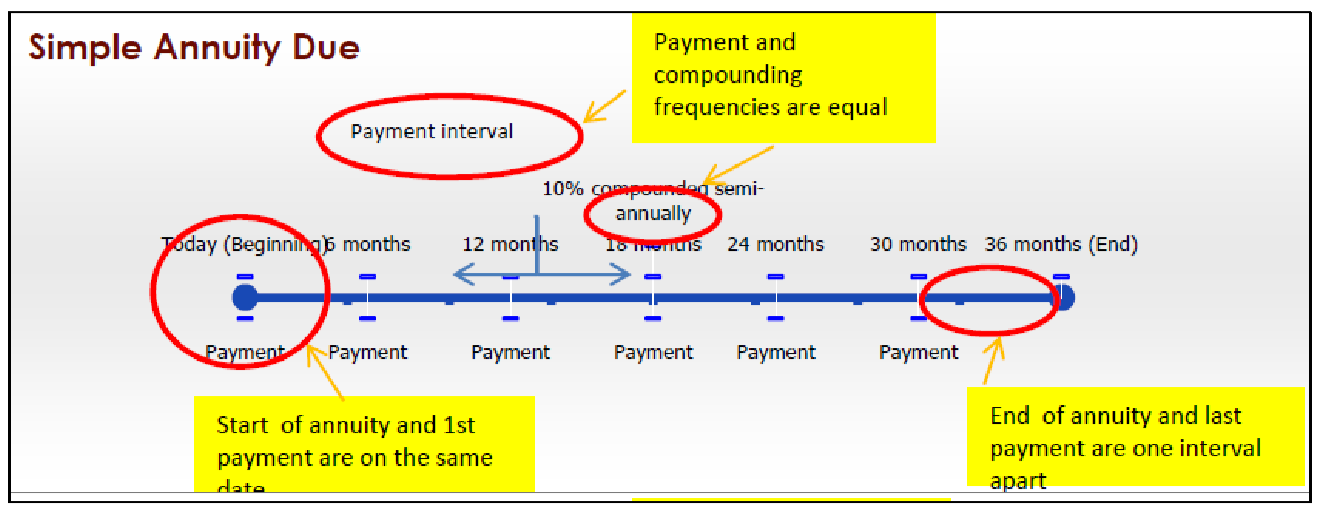
$clipboard_e4261d6176a026de70ada501d33c26522.png$

Vencimiento de anualidad simple

Una simple anualidad adeudada tiene las siguientes características:

Los pagos se realizan al inicio de los intervalos de pago, y las frecuencias de pago y capitalización son iguales.
El primer pago ocurre en la misma fecha que el inicio de la anualidad.
El último pago ocurre un intervalo de pago antes del final de la anualidad.

Por ejemplo, la mayoría de los arrendamientos de automóviles son simples anualidades vencidas, donde los pagos se realizan mensualmente y las tasas de interés se componen mensualmente. No obstante, el día en que firme el contrato de arrendamiento es cuando debe realizar su primer pago mensual.

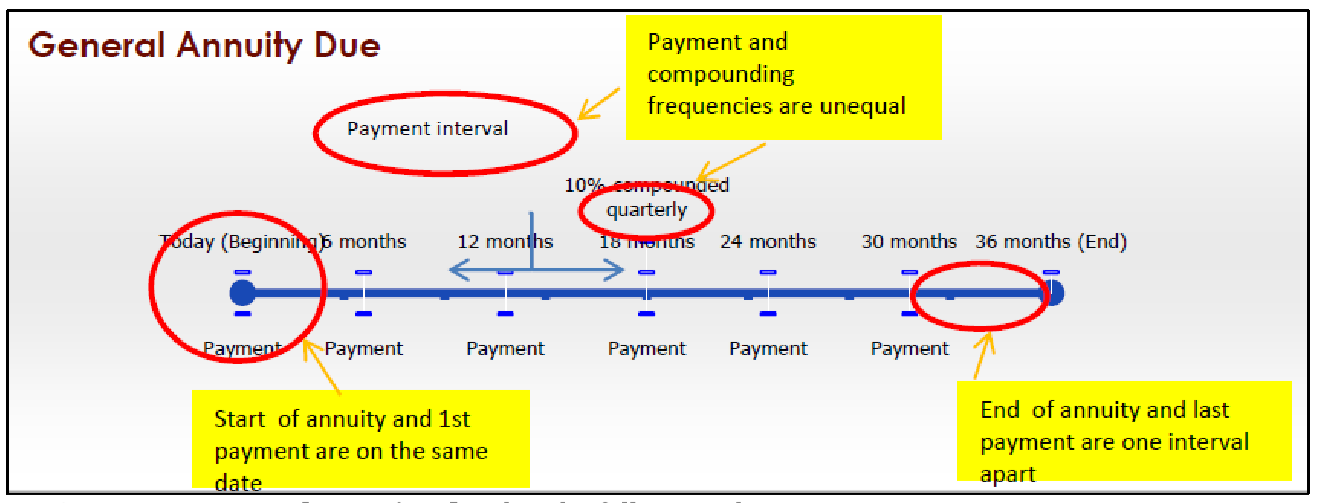
$clipboard_e26d04f5a2f646857c41be019daed72f3.png$

Anualidad General Vencida.

Una anualidad general adeudada tiene las siguientes características:

Los pagos se realizan al inicio de los intervalos de pago, y las frecuencias de pago y capitalización son desiguales.
El primer pago ocurre en la misma fecha que el inicio de la anualidad.
El último pago ocurre un intervalo de pago antes del final de la anualidad.

Por ejemplo, muchas inversiones, como su RRSP, son anualidades generales adeudadas donde los pagos (contribuciones) generalmente se realizan mensualmente pero los intereses se componen de otra manera, como anualmente. Además, cuando la mayoría de las personas inician un RRSP lo pagan el día en que lo configuran, lo que significa que su RRSP comienza con el primer pago depositado.

En la siguiente tabla se resumen los cuatro tipos de anualidades y sus características para facilitar la referencia.

Tipo de anualidad	Momento de los pagos en un intervalo de pago	Frecuencia de pago y frecuencia de composición	Inicio de Anualidad y Primer Pago Misma Fecha?	Fin de Anualidad y Último Pago ¿Misma Fecha?
Anualidad Simple Ordinaria	Fin	Iguales	No, primer pago un intervalo después	Sí
Anualidad General Ordinaria	Fin	Desiguales	No, primer pago un intervalo después	Sí
Vencimiento de anualidad simple	Comienzo	Iguales	Sí	No, último pago un intervalo anterior
Vencimiento de Anualidad General	Comienzo	Desiguales	Sí	No, último pago un intervalo anterior

Caminos hacia el éxito

Uno de los aspectos más desafiantes de las anualidades es reconocer si la anualidad con la que está trabajando es ordinaria o vencida. Esta distinción juega un papel crítico en la selección de fórmulas más adelante en este capítulo. Para ayudarle a reconocer la diferencia, la siguiente tabla resume algunas palabras clave junto con aplicaciones comunes en las que puede aparecer la anualidad.

Tipo	Palabras o Frases Clave	Aplicaciones Comunes
Ordinario	-... los pagos están al final... -... los pagos no inician hoy... -... los pagos son posteriores... -... primer pago siguiente intervalo...	- préstamos bancarios de cualquier tipo - hipotecas - bonos - Plan de Pensiones de Canadá (CPP)
Debido	-... los pagos están al inicio... -... los pagos comienzan hoy... -... los pagos son anticipados... -... primer pago hoy... -... los pagos empiezan ahora...	- cualquier tipo de arrendamiento - cualquier tipo de renta - RRSP (generalmente) - cuotas de membresía - seguro

Anualidades versus pagos únicos

Para pasar de los pagos únicos en el Capítulo 9 a las anualidades en este capítulo, es necesario realizar varias adaptaciones:

Monto de Pago de Anualidad (PMT). Esta variable no se utilizó en ninguna de las fórmulas introducidas en el Capítulo 9 o en el Capítulo 10, aunque se introdujo brevemente cuando la Sección 9.2 al demostrar las funciones de la calculadora. Observe que en los dos capítulos anteriores esta variable se fijó en cero para cada pregunta, ya que cada pago no formaba parte de una anualidad. Los cálculos de anualidades requieren que se ate un valor a esta variable en las fórmulas y cuando se utiliza tecnología como la calculadora BAII+.
Frecuencia de Pago o Pagos por Año (PY). Para pagos únicos, esta variable no se presentó en ninguna de las fórmulas de los dos capítulos anteriores. También se introdujo en la Sección 9.2 como un botón de calculadora con el requisito de que se establezca automáticamente como una variable nula que coincida con la frecuencia de composición (CY). Cuando trabajas con anualidades, un valor real para$PY$ está determinado por la frecuencia de pago. Para las anualidades simples$PY$ sigue siendo lo mismo que$CY$, mientras que las variables son diferentes para las anualidades generales.
Convenio de Signo de Flujo de Efectivo en la Calculadora. Ahora se vuelve crítico asegurar la correcta aplicación de la convención de señales de flujo de caja en la calculadora; de no hacerlo, se obtendrá una respuesta incorrecta. Por ejemplo, si pides dinero prestado y luego haces pagos de anualidades sobre él, ingresas el valor presente ($PV$) como positivo (recibiste el dinero) mientras ingresas los pagos de anualidad como negativos (pagaste el dinero al banco). Esto da como resultado que los saldos futuros se hagan más pequeños y que debas menos dinero. Si inadvertidamente ingresa el pago de anualidad como un número positivo, esto significaría que está pidiendo prestado más dinero al banco para que su saldo futuro aumente y adeudaría más dinero. ¡Estas dos respuestas son muy diferentes!
Definición y Computación de N. Cuando se trabajó con pagos únicos,$N$ se definió como el número total de compuestos a lo largo del plazo de la transacción financiera. Cuando se trabaja con anualidades,$N$ se define como el número total de pagos a lo largo del plazo de la anualidad. La calculas usando la Fórmula 11.1.

La Fórmula

$clipboard_e3982a10b50df004be3651e1a0b8b9776.png$

Fórmula 11.1

Cómo funciona

En un préstamo de dos años con pagos mensuales y capitalización semestral, la frecuencia de pago es mensual, o 12 veces al año. Con un plazo de dos años, eso hace N = 2 × 12 = 24 pagos. Obsérvese que el cálculo de N para una anualidad no implica la frecuencia de capitalización.

Adaptación de cronogramas para incorporar anualidades

Las preguntas sobre anualidades pueden involucrar muchos pagos. Por ejemplo, en una hipoteca típica a 25 años con pagos mensuales, eso sería de 25 × 12 = 300 pagos en total. ¿Cómo dibujarías una línea de tiempo para estos? Claramente, no sería práctico sacar 300 pagos.

Un buen cronograma de anualidad debe ilustrar el valor presente ($PV$), el valor futuro ($FV$), el número de pagos de anualidad ($N$), la tasa de interés nominal ($IY$), la frecuencia de capitalización ($CY$), el pago de anualidades ($PMT$) y la frecuencia de pago ($PY$). Una de estas variables será la desconocida.

Además, un buen cronograma requiere una clara distinción entre anualidades ordinarias y anualidades adeudadas. END se utiliza para representar anualidades ordinarias, ya que los pagos ocurren al final del intervalo de pago. De igual manera, BGN se utiliza para representar las anualidades adeudadas, ya que los pagos ocurren al inicio del intervalo de pago. La siguiente figura ilustra el formato adaptado de la línea de tiempo de anualidad.

$clipboard_e16e2147badf8e54f249103053c617a54.png$

Algunas veces una variable cambiará a la parte del período de una anualidad, en cuyo caso la línea de tiempo debe dividirse en dos o más segmentos. Cuando se utiliza esta estructura, en cualquier segmento de tiempo$PMT$ se interpreta que el pago de anualidad tiene la misma cantidad en el mismo intervalo de pago continuamente a lo largo de todo el segmento. El número de pagos de anualidades$N$ no aparece directamente en el cronograma ya que es el resultado de una fórmula. Sin embargo, sus dos componentes (Años y PY) se dibujan en la línea de tiempo.

Cómo funciona

Se utiliza una hipoteca para ilustrar este nuevo formato. Por ahora, enfocarse estrictamente en las variables y cómo ilustrarlas en una línea de tiempo. No te centres en ningún cálculo hipotecario todavía.

Según la introducción del capítulo, compró una vivienda de $150,000 ($PV$) con una hipoteca a 25 años (Años). La tasa hipotecaria es del 5% ($IY$) compuesta semestralmente ($CY$= 2), y los pagos mensuales ($PY$= 12) son $872.41 ($PMT$).
Después de 25 años serás dueño de tu casa y por lo tanto no te quedará saldo. Esto establece el valor futuro en $0 ($FV$).
Las hipotecas son de naturaleza ordinaria, es decir, que los pagos ocurren al final de los intervalos de pago (FIN). La siguiente figura coloca todos estos elementos hipotecarios en el nuevo formato de línea de tiempo. Una vez que haya dibujado la línea de tiempo, puede determinar lo siguiente:

$clipboard_e91ba49fb9126eb6eda5eb3ae7f588d73.png$

El número de pagos ($N$), que calculas usando la Fórmula 11.1. Ya que ambos$PY$ y Años son conocidos, tienes$N$ = 25 × 12 = 300.
Si la anualidad es simple o general, lo que depende de la parte$PY$ inferior de la línea de tiempo y$CY$ por encima de la línea de tiempo. Si coinciden, la anualidad es simple; si difieren, como en este ejemplo, es general.

Cosas a tener en cuenta

La palabra “pago” a menudo confunde a la gente porque tiene dos interpretaciones. Podría significar ya sea “pago único”, como en el Capítulo 9, o r “pago de anualidad”, que se entiende en este capítulo. Para interpretar correctamente esta palabra, recordar las características de un pago de anualidad y determinar si la situación en cuestión coincide con los criterios. Revisemos dos ejemplos que ilustran este punto:

Supongamos que John le debe a María tres pagos de $200 adeudados dentro de dos meses, cinco meses y once meses a partir de ahora. En este caso, la palabra “pago” significa “pago único” porque los pagos son iguales (todos $200) y se conocen los periodos de tiempo, pero no son periódicos (los intervalos de pago son desiguales) ni continuos (ya que no existen periodos, no hay continuidad). Trabajar con estos pagos requiere aplicar las fórmulas y técnicas fr om Capítulo 9.
Supongamos que John le debe a Julia tres pagos de $200 adeudados en tres meses, seis meses y dentro de nueve meses. En este caso, la palabra “pago” significa “pago de anualidad” porque los pagos son iguales (todos los $200), periódicos (cada trimestre) y continuos (ocurriendo cada trimestre sin interrupción), y tienen un marco de tiempo especificado (más de nueve meses). Trabajar con estos pagos permite aplicar las fórmulas y técnicas de este capítulo.

En definitiva, en caso de duda se puede resolver cualquier duda que implique el valor del dinero en el tiempo utilizando las fórmulas y técnicas del Capítulo 9. Las fórmulas de anualidad introducidas en la siguiente sección solo permiten llegar a la misma respuesta con mucho menos cálculo.

Colaboradores y Atribuciones

Template:ContribBusiMathOlivier

Search

Text Color

Text Size

Margin Size

Font Type