12.2: Anualidades de crecimiento constante
- Page ID
- 110647
Muchos expertos recomiendan que ahorres alrededor del 10% de tus ingresos anuales en tus contribuciones de RRSP. Como la mayoría de las personas, cuando egresas de colegio o universidad, tu empleador te ofrecerá un salario inicial que suele estar en el extremo inferior de su escala salarial. En la mayoría de las empresas, usted es elegible para recibir aumentos anuales de acuerdo con una estructura de pago predeterminada o a través de revisiones de desempeño. Esto representa un ingreso anual que siempre sube. Como resultado, sus contribuciones de RRSP siempre deben aumentar anualmente también.
Todos los cálculos de anualidades hasta el momento han permitido contribuciones fijas únicamente. De manera más realista, en muchas situaciones financieras, como su RRSP, los pagos de anualidades deben aumentar constantemente de forma regular. Para esta situación es necesario estudiar anualidades de crecimiento constante.
El concepto de crecimiento constante
Una anualidad de crecimiento constante es una anualidad en la que cada pago de anualidad se incrementa en un porcentaje fijo. La cifra aquí ilustra un pago inicial de $1,000 que crece 5% con cada pago posterior.
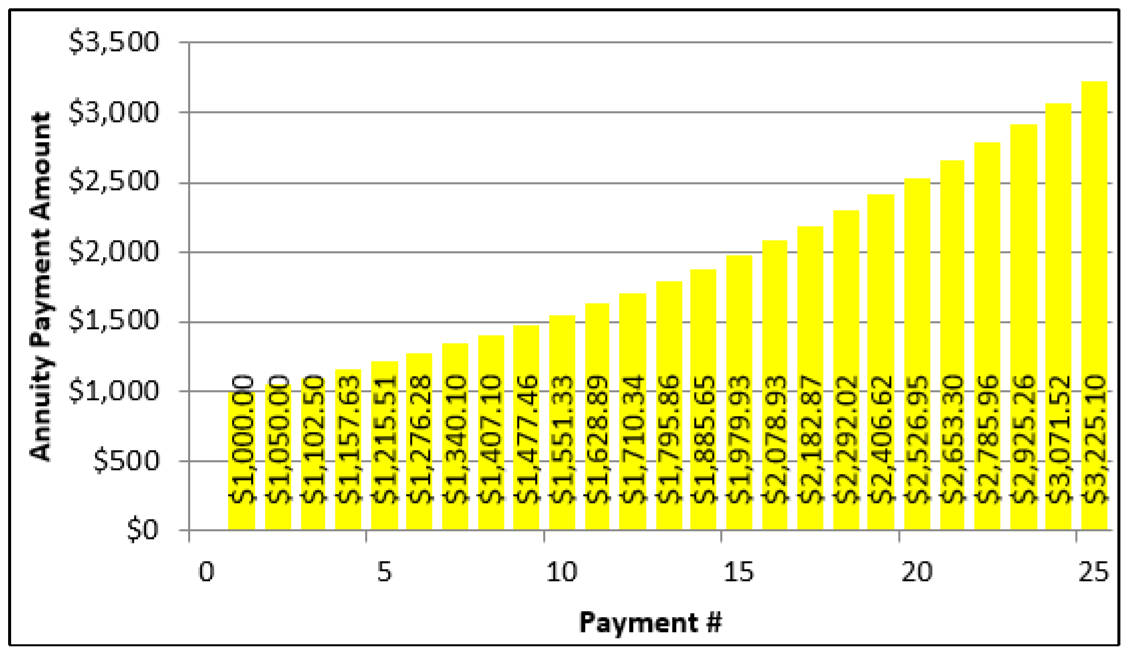
Además de sus contribuciones de RRSP, los pagos de anualidades se incrementan regularmente en muchas situaciones:
- Al sacar de sus ahorros para la jubilación, debe aumentar sus pagos cada año para mantenerse al día con el costo de vida. Esta creciente demanda de tu fondo de retiro debe ser tenida en cuenta en un plan de ahorro RRSP adecuado.
- Los pagos del Plan de Pensiones de Canadá y el Seguro de Vejez, junto con la mayoría de los planes de pensiones de empresas privadas, aumentan anualmente para igualar la tasa de inflación.
El cambio en cada pago es un porcentaje fijo y por lo tanto representa un cambio porcentual en el pago de anualidad. Esto puede ser representado por el símbolo de cambio porcentual,\(∆\%\), utilizado en la Sección 3.1. Esta variable representa el cambio porcentual periódico, donde el periodo es consistente con el intervalo de pago. Por lo tanto, si los pagos son mensuales entonces la variable de cambio porcentual necesita expresarse como el cambio porcentual mensual.
El impacto del crecimiento constante en el pago de anualidades
Para entender cómo el crecimiento constante afecta la variable de pago de anualidades, eche un vistazo a cómo se representan los cuatro primeros pagos en cualquier anualidad de crecimiento constante. Recordemos en anualidades que\(N\) representa el número de pagos, por lo tanto:
\(N = 1\): Primer pago\(= PMT = PMT(1 + ∆\%)^{N – 1}\) (ya que\(N = 1\), esto produce un exponente cero sobre el cambio porcentual)
\(N = 2\): Segundo pago\(= PMT (1 + ∆\%) = PMT(1 + ∆\%)^{N – 1}\)
\(N = 3\): Tercer pago\(= PMT (1 + ∆\%)(1 + ∆\%) = PMT (1 + ∆\%)^2 = PMT(1 + ∆\%)^{N – 1}\)
\(N = 4\): Cuarto pago\(= PMT (1 + ∆\%)(1 + ∆\%)(1 + ∆\%) = PMT (1 + ∆\%)^3 = PMT(1 + ∆\%)^{N – 1}\)
Observe que cada pago de anualidad en última instancia está representado por\(PMT(1 + ∆\%)^{N – 1}\) independientemente del número de pagos de anualidad realizados.
El impacto del crecimiento constante en la tasa de interés de anualidad
Debe ajustar la tasa de interés periódica de anualidad para aislar el crecimiento en la anualidad de los intereses, ya que el crecimiento en los pagos de anualidades ya se refleja en el\(PMT(1 + ∆\%) ^ {N — 1}\) anterior. En el transcurso de cualquier periodo, los intereses se componen a una tasa calculada como\(1 + i\). Por otro lado, las contribuciones a lo largo del mismo periodo de tiempo crecen por\(1 + ∆\%\). Por lo tanto, el interés en la cuenta crece más que el crecimiento de las contribuciones por una tasa que se calcula por:
\[\dfrac{(1+i)}{(1+\Delta \%)}-1 \nonumber \]
Para fines ilustrativos, asumir una anualidad con una tasa de interés periódica del 10% y una tasa de crecimiento periódico del 5%. Aplicar el cálculo anterior:
\[\dfrac{1+0.1}{1+0.05}-1=\dfrac{1.1}{1.05}-1=0.047619 \nonumber \]
Por lo tanto, cada periodo el crecimiento neto atribuible únicamente a los intereses representa una capitalización periódica de 4.7619% y no del 10%. Esta tasa de interés, a veces llamada tasa neta, debe reemplazar la tasa de interés periódica que utiliza en todas las fórmulas de anualidades.
La Fórmula
A continuación se muestran las cuatro fórmulas para el valor futuro y el valor presente de las cuotas ordinarias y anualidades, incorporando el concepto de crecimiento constante. Observe en cada fórmula que la tasa de interés periódica se cambia a tasa neta. La fórmula de cambio porcentual en el denominador no requiere del\(\dfrac{CY}{PY}\) exponente ya que la variable ya se expresa en los mismos términos periódicos que los pagos.
- Fórmulas de Valor Futuro. El pago de anualidad se modifica para incorporar el crecimiento en los pagos de\(PMT\) a\(PMT(1 + ∆\%)^{N – 1}\) como se ha ilustrado anteriormente. El primer pago tiene crecimiento cero, lo que da como resultado que un exponente tenga un periodo de crecimiento menor que el número de pagos realizados.
- Fórmulas de valor presente. Al devolver la anualidad a su inicio, esto representa el pago número 0 ya que aún no se ha producido un primer pago. La aplicación de la\(PMT(1 + ∆\%)^{N – 1}\) fórmula da como resultado\(PMT(1+\Delta \%)^{0-1}=PMT(1+\Delta \%)^{-1}=\dfrac{PMT}{1+\Delta \%}\), que luego sustituye\(PMT\) en la fórmula.

Fórmula para Valor Futuro y Valor de Crecimiento - 12.1, 12.2, 12.3, 12.4
Haga las siguientes notas sobre las variables:
- \(PMT\). Cada pago aumenta constantemente en una anualidad de crecimiento constante. Por lo tanto, el primer pago es el valor claramente identificable. Para determinar el valor de cualquier otro pago, utilice la fórmula\(PMT(1+\Delta \%)^{N-1}\), como se ha ilustrado anteriormente. Por ejemplo, si un pago de $1,000 está creciendo al 5% y es necesario conocer el valor del décimo pago, se calcula como\(\$ 1,000(1+0.05)^{10-1}=\$ 1,551.33\).
- \(i\). La tasa de interés resultante de la Fórmula 9.1, convertida para igualar el intervalo de pago si es necesario. La tasa de interés periódica se ajusta para reflejar la tasa neta dividiéndola por\(1 + ∆\%\).
- \(∆\%\). El cambio porcentual periódico coincidiendo con el intervalo de pago entre cada pago sucesivo en la anualidad. Si los pagos se realizan trimestralmente, entonces se requiere el cambio porcentual por trimestre. El valor de\(∆\%\) en estas fórmulas se restringe a un valor menor que la tasa de interés periódica equivalente\(i\) (donde\(i\) se expresa como la tasa de interés por intervalo de pago). Situaciones donde\(\Delta \% \geq(1+i)^{\frac{CY}{PY}}-1\) están más allá del alcance de este libro de texto. Si\(∆\%\) se le asigna un valor de 0% entonces estas fórmulas vuelven a las Fórmulas 11.2 a 11.5, respectivamente. De ahí que a las fórmulas del Capítulo 11 se les haga referencia a veces como fórmulas de anualidad de crecimiento cero y representan versiones simplificadas de estas fórmulas de anualidad completas.
Cómo funciona
Siga los mismos pasos discutidos para el valor futuro en la Sección 11.2 y los pasos para el valor presente en la Sección 11.3. La única diferencia notable es que se debe identificar la tasa de crecimiento periódico para el pago de anualidad y, por supuesto, utilizar las nuevas Fórmulas 12.1 a 12.4. La siguiente figura ilustra una línea de tiempo típica cuando se trata de un crecimiento constante. Anote el\(∆\%\) después del tipo de anualidad y que solo uno de\(FV_{ORD}\),,\(FV_{DUE}\)\(PV_{ORD}\), o\(PV_{DUE}\) alguna vez aparece en la línea de tiempo.

Las aplicaciones más comunes que involucran anualidades de crecimiento constante requieren que calcule el valor futuro, el valor presente o el pago de la primera anualidad. En los dos primeros casos, usa Fórmulas 12.1 a 12.4 para resolver para\(FV\) y\(PV\). Si el primer pago de anualidad es la variable desconocida, puede reorganizar cualquiera de las Fórmulas 12.1 a 12.4 algebraicamente para aislarlas\(PMT\) según sea necesario.
Notas Importantes
La mayoría de las calculadoras financieras, incluyendo el Texas Instruments BAII Plus, no están preprogramadas con anualidades de crecimiento constante. Están diseñados para manejar anualidades de pago fijo únicamente.
Dicho esto, en la web o en tus lecturas puedes encontrarte con métodos que te muestran cómo adaptar tu entrada de calculadora para “engañar” a la calculadora. Es importante tener en cuenta que estos métodos son generalmente complejos, requiriendo memorizar muchas adaptaciones y modificaciones condicionales. Las salidas no son necesariamente correctas a menos que se adapten más. En definitiva, estos trucos no son recomendables. Este libro de texto resuelve anualidades de crecimiento constante solo usando fórmulas y a través de la plantilla Excel.
Caminos hacia el éxito
Si bien toda la discusión ha sido sobre el crecimiento, también se pueden utilizar estas fórmulas en situaciones que implican una reducción constante ya que el requerimiento de\(\Delta \%<(1+i)^{\frac{CY}{PY}}-1\) sigue siendo cierto. Utilizar un valor negativo para la tasa de crecimiento en todos los cálculos.
Adicionalmente, si deseas conocer el valor total de los pagos de anualidades en una anualidad de crecimiento constante, puedes usar la Fórmula 11.2 con algunas adaptaciones:
- Tratar el primer pago como el monto del pago de anualidad o\(PMT\).
- Sustituir la tasa de crecimiento periódico por la tasa de interés periódica equivalente mientras fija\(CY\) y\(PY\) ambas a 1. Esto elimina al\(\dfrac{CY}{PY}\) exponente.
- Conservar usando\(N\) como número de pagos.
Así, sustituir y simplificar produce el siguiente cálculo:
\[\text { Sum of constant growth payments }=PMT\left[\dfrac{[(1+\Delta \%)]^{\mathrm{N}}-1}{\Delta \%}\right] \nonumber \]
Si un pago de anualidad se incrementa en $5 cada vez de $100 a $105 a $110 a $115, ¿representa esto una situación de crecimiento constante?
- Contestar
-
No. Un crecimiento constante está representado por un crecimiento porcentual fijo, no un crecimiento fijo en dólares.
Bradford tiene 27 años y comienza a invertir $3,000 anuales en su RRSP ganando 9% compuesto anualmente. Decide que cada año aumentará sus contribuciones en 2.5%. Calcular el valor de vencimiento a los 65 años tanto para una anualidad ordinaria como para una anualidad adeudada.
Solución
Si cada pago aumenta en un porcentaje fijo, entonces esta es una anualidad de crecimiento constante. Calcular dos valores de vencimiento, uno para la anualidad ordinaria, o\(FV_{ORD}\), y otro para la anualidad adeudada, o\(FV_{DUE}\).
Lo que ya sabes
Paso 1:
Hay contribuciones anuales con una tasa de interés compuesta anual. El pago inicial crea una anualidad simple de crecimiento constante debido, mientras que los pagos finales crean una anualidad ordinaria simple de crecimiento constante. La línea de tiempo se encuentra a continuación.

Paso 2:
Ambas anualidades:\(PV\) = $0,\(IY\) = 9%,\(CY\) = 1,\(PMT\) = $3,000,\(PY\) = 1, Años = 38,\(∆\%\) = 2.5%
Cómo Llegarás Allí
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Con\(PV\) = $0, omita este paso.
Paso 5:
Aplicar la Fórmula 11.1 y las Fórmulas 12.1 y 12.2.
Realizar
Paso 3:
\(i=9 \% / 1=9 \%\)
Paso 5:
\(N=1 \times 38=38 \text { payments } \)
\[FV_{ORD}=\$ 3,000(1+0.025)^{37}\left[\dfrac{\left [\dfrac{(1+0.09)^{\frac{1}{1}}}{(1+0.025)^{\frac{1}{1}}} \right ]^{38}-1}{\dfrac{(1+0.09)^{\frac{1}{1}}}{(1+0.025)^{\frac{1}{1}}}-1}\right]=\$ 1,102,199.91 \nonumber \]
\[FV_{DUE}=\$ 1,102,199.91 \times(1+0.09)^{\frac{1}{1}}=\$ 1,201,397.90 \nonumber \]
Las 38 contribuciones ascienden a una aportación principal total de $186.681.89. El valor de vencimiento de la anualidad ordinaria es de $1,102,199.91 y la anualidad adeudada es un compuesto superior en $1,201,397.90.
¿Cuánto dinero se requiere hoy para financiar una anualidad de 10 años ganando 5.6% compuesta trimestralmente donde el primer pago mensual será de $2,000 y cada pago crecerá 0.2%? Calcular tanto como anualidad ordinaria como anualidad adeudada.
Solución
Si cada pago aumenta en un porcentaje fijo, entonces esta es una anualidad de crecimiento constante. Calcular dos cantidades principales, una para la anualidad ordinaria, o\(PV_{ORD}\), y otra para la anualidad adeudada, o\(PV_{DUE}\).
Lo que ya sabes
Paso 1:
Hay pagos mensuales con una tasa de interés compuesta trimestral. Los pagos iniciales crean una anualidad general de crecimiento constante debido, mientras que los pagos finales crean una anualidad ordinaria de crecimiento constante general.
La línea de tiempo aparece a continuación.

Paso 2:
Ambas anualidades:\(FV\) = $0,\(IY\) = 5.6%,\(CY\) = 4,\(PMT\) = $2,000,\(PY\) = 12, Años = 10,\(∆\%\) = 0.2%
Cómo Llegarás Allí
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Con\(FV\) = $0, omita este paso.
Paso 5:
Aplicar Fórmula 11.1 y Fórmulas 12.3 y 12.4.
Realizar
Paso 3:
\(i=5.6 \% / 4=1.4 \%\)
Paso 5:
\(N=12 \times 10=120 \text { payments } \)
\[ PV_{ORD}=\dfrac{\$ 2,000}{1+0.002}\left[\dfrac{1-\left[\dfrac{(1+0.002)}{(1+0.014)^{\frac{4}{12}}}\right]^{120}}{\dfrac{(1+0.014)^{\frac{4}{12}}}{(1+0.002)}-1}\right]=\$ 205,061.74 \nonumber \]
\[PV_{DUE}=\$ 205,061.7409 \times(1+0.014)^{\frac{4}{12}}=\$ 205,061.7409 \times 1.004645=\$ 206,014.26 \nonumber \]
Los 120 pagos cada uno aumentaron en 0.2% montos a un pago total de $270,944.49. Para financiar estos pagos, una anualidad ordinaria de crecimiento constante requiere hoy 205,061.74 dólares, mientras que una anualidad de crecimiento constante adeudada requiere un poco más, igualando $206,014.26 porque el primer pago se retira de inmediato.
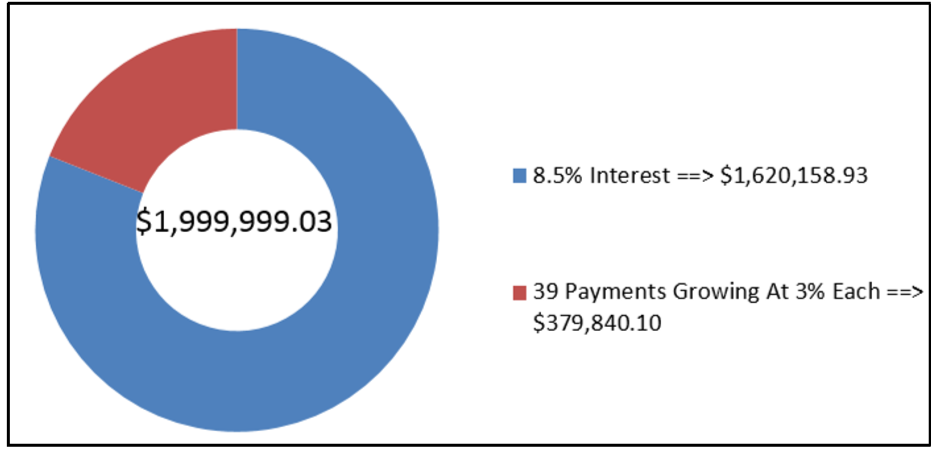
Después de una discusión con su asesor financiero el 28 de febrero de 2012, Jennifer ha determinado que necesita 2 millones de dólares en su RRSP cuando se jubila el 28 de febrero de 2051. Ella ha decidido comenzar a hacer contribuciones anuales a su RRSP a partir del 28 de febrero de 2013, y crecer esas contribuciones un 3% cada año. Si su RRSP puede ganar 8.5% compuesto anualmente, ¿en qué cantidad debería hacer su primer aporte?
Solución
Si cada pago aumenta en un porcentaje fijo, entonces esta es una anualidad de crecimiento constante. Calcular el monto de su primer pago de anualidad (\(PMT\)).
Lo que ya sabes
Paso 1:
Hay contribuciones anuales al final del intervalo con una tasa de interés compuesta anual. Por lo tanto, se trata de una anualidad ordinaria simple de crecimiento constante.
La línea de tiempo aparece a continuación.

Paso 2:
\(PV\)= $0,\(FV_{ORD}\) = $2,000,000,\(IY\) = 8.5%,\(CY\) = 1,\(PY\) = 1, Años = 39,\(∆\%\) = 3%
Cómo Llegarás Allí
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
Con\(PV\) = $0, omita este paso.
Paso 5:
Aplicar Fórmula 11.1 y Fórmula 12.1. Una vez que haya sustituido y simplificado esta fórmula, reorganícela para\(PMT\).
Paso 3:
\(i=8.5 \% / 1=8.5 \%\)
Paso 5:
\(N=1 \times 39=39 \text { payments } \)
\[\$ 2,000,000=PMT(1+0.03)^{38}\left[\dfrac{\left[\dfrac{(1+0.085)^{\frac{1}{3}}}{(1+0.05)^{\frac{1}{1}}}\right]^{39}-1}{\dfrac{(1+0.055)^{\frac{1}{1}}}{(1+0.03)^{\frac{1}{1}}}-1}\right] \nonumber \]
\[\$ 2,000,000=PMT(3.074783)\left[\dfrac{6.605154}{0.053398}\right] \nonumber \]
\[\begin{align*} \$ 2,000,000&=PMT(380.340030) \\ \$ 5,258.45&=PMT \end{align*} \nonumber \]
El primer pago de Jennifer es de $5,258.45 y luego aumentó un 3% cada año para sus 39 pagos para proporcionar suficiente capital para lograr su objetivo financiero de $2,000,000. Tenga en cuenta que debido al redondeo del primer pago de anualidad, de hecho termina marginalmente por debajo de su meta por la cantidad de $0.97.