12.3: Perpetuidades
- Page ID
- 110646
Algunas de las becas que se ofrecen a los estudiantes de tu universidad fueron creadas hace décadas, sin embargo, estas becas continúan pagando dinero a los estudiantes todos y cada uno de los años. ¿De dónde viene todo el dinero? ¿Alguien otorgó un fondo de dotación tremendamente grande todos esos años atrás para sostener la beca a lo largo de décadas? ¿O un individuo u organización de apoyo simplemente lo paga de su bolsillo cada año? ¿Cómo es posible que estas becas se paguen a lo largo de todos los años pasados y todos los años previsibles?
¿Qué harías si ganaras un gran premio de lotería como Lotto 6/49 o Lotto Max? Los titulares de hoy muestran continuamente a ganadores de lotería que ganan “el grande”, convirtiéndose en millonarios de la noche a la mañana. Con sus ganancias recién descubiertas, se apresuran a comprar casas millonarias y vehículos de lujo y disfrutar de los placeres de la vida. En algún momento poco después, se cuentan historias sobre cómo estos millonarios se declaran en bancarrota. Y si alguien le hubiera dicho a estas personas que en lugar de gastar el dinero todo a la vez, podrían invertirlo y usar el interés para vivir para siempre; generaciones enteras de su familia podrían beneficiarse de las ganancias. Imagínese: si invierte 5 millones de dólares al 5% de interés, ganaría 250.000 dólares de interés cada año que podría retirar sin cesar.
Estos escenarios resaltan la importancia de las perpetuidades, que son anualidades que tienen un término infinito. A tu nivel individual, cualquier suma de dinero que inviertas a perpetuidad puede ser utilizada para generar ingresos para siempre. A nivel profesional, muchas empresas y organizaciones sin fines de lucro como clubes deportivos establecen programas de becas y becas para sus empleados, miembros o clientes. En algunos contratos, los pagos como las regalías continúan para siempre. Algunas acciones divididas tienen su precio determinado por cantidades de dividendos futuros indefinidos.
En esta sección se explora el concepto de perpetuidad. Calcularás la inversión requerida para mantener una perpetuidad junto con el monto del pago.
¿Qué son las Perpetuidades?
Una perpetuidad es un tipo especial de anualidad que tiene pagos fijos y regulares continuando indefinidamente. Si el principal de la inversión nunca se retira, entonces los intereses devengados en cada periodo pueden ser retirados sin afectar las ganancias futuras por intereses de la inversión. Por lo tanto, la anualidad sigue ganando la misma cantidad de intereses en todos y cada uno de los intervalos futuros y puede pagar intereses para siempre. ¿Cómo puede un solo depósito de principal sostener una cantidad infinita de pagos? Matemáticamente, el dinero que ocurre en un futuro lejano se vuelve inservible cuando se vuelve a la actualidad, donde no tiene valor.
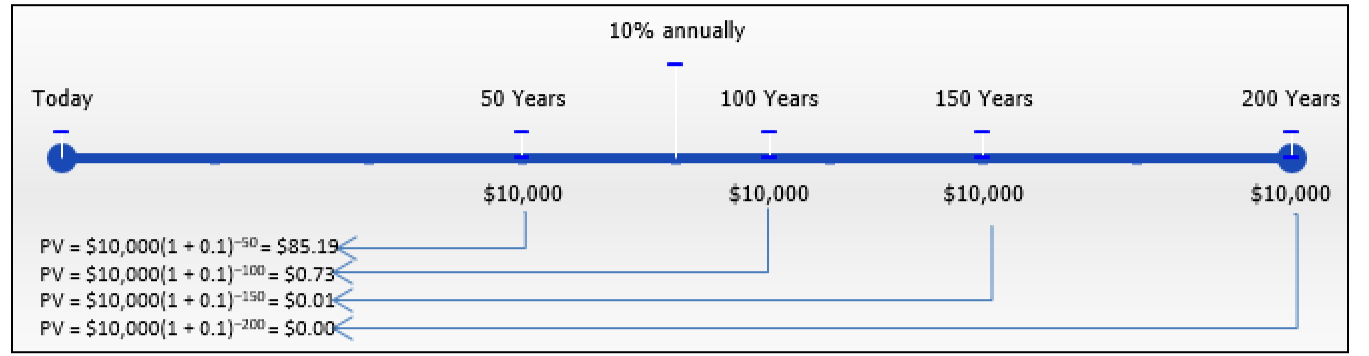
Para ilustrar el punto de que el dinero no tiene valor hoy en día, la cifra aquí calcula algunos valores actuales de 10 mil pagos que ocurren en el futuro. A través de los diversos cálculos, observe que cuando los pagos ocurren más adelante en el futuro el valor presente disminuye prácticamente a nada. De hecho, después de unos 160 años los 10.000 dólares llegan a valer casi 0 dólares hoy en día. Cualquier pago realizado después de este punto en el tiempo da como resultado adiciones tan minúsculas al valor actual que, en esencia, realmente no tienen más impacto. Bajo esta premisa, entonces es posible determinar un valor hoy que es equivalente al flujo futuro infinito de pago de anualidades.
Perpetuidades ordinarias y perpetuidades debidas
Una perpetuidad es un tipo especial de anualidad. Viene tanto en el tipo de vencimiento ordinario como de anualidad. Además, la frecuencia de pago y la frecuencia de capitalización crean una estructura de anualidad simple o general. Las perpetuidades pueden incluso ocurrir después de un período de aplazamiento y, por lo tanto, las perpetuidades diferidas son posibles.
Aquí aparece una línea de tiempo típica para perpetuidad. Es idéntico a cualquier otro cronograma de anualidad excepto por dos características distintivas:

- Periodo de Tiempo Futuro. En lugar de que se indique un período de tiempo específico en el lado derecho de las líneas de tiempo, aparece la palabra “Para siempre”, para representar la naturaleza infinita de la perpetuidad.
- Equivalencia de\(FV\) y\(PV\). El valor futuro de la perpetuidad es el mismo que el valor presente ya que solo se pagan los intereses y nunca se toca el principal.
La Fórmula
Al igual que las fórmulas de anualidad, las fórmulas de perpetuidad están diseñadas para acomodar anualidades tanto simples como generales a través del\(\dfrac{CY}{PY}\) exponente, lo que asegura que el intervalo de composición coincida con el intervalo de pago. Estas nuevas fórmulas representan versiones simplificadas de las Fórmulas 11.4 y 11.5. Para ilustrar, recuerde la Fórmula 11.4:
\[PV_{ORD}=PMT\left[\dfrac{1-\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^{N}}{(1+i)^{\frac{CY}{PY}-1}}\right] \nonumber \]
Al mirar al numerador, como\(N\) sea viene cada vez más grande se\(\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^{N}\) acerca a un valor de cero, que efectivamente lo elimina de la ecuación. Esto deja un numerador de 1 sobre el denominador.

Cómo funciona
Los pasos requeridos para resolver por el valor presente de una perpetuidad permanecen esencialmente inalterados de resolver por el valor presente de cualquier anualidad. Estos pasos, introducidos en la Sección 11.3, son revisados para el caso de perpetuidad:
Paso 1: Identificar el tipo de perpetuidad. Dibuja una línea de tiempo para visualizar la pregunta.
Paso 2: Identificar las variables que pueden conocerse, incluyendo\(IY, CY, PMT, PY\), y cualquiera\(PV_{ORD}\) o\(PV_{DUE}\). Si\(PV_{DUE}\) se conoce a\(PV_{ORD}\) o, a continuación, establezca el\(FV\) a la misma cantidad. Si no se conoce ningún valor presente, entonces se establece\(FV\) en $0, ya que el dinero en un futuro lejano no tiene valor. A diferencia de las anualidades regulares, no es necesario identificar Años debido a la ausencia de N en todos los cálculos de perpetuidad.
Paso 3: Usa la Fórmula 9.1 para calcular\(i\).
Paso 4: Nunca requieres este paso ya que el\(FV\) está ubicado tan lejos en el futuro que automáticamente puedes determinar que su valor presente es igual a cero.
Paso 5: Para calcular el valor presente, aplique ya sea la Fórmula 12.5 o la Fórmula 12.6, dependiendo del tipo de perpetuidad.
Al igual que con las anualidades regulares, si se trata de una perpetuidad diferida entonces debe modificar estos procedimientos como lo haría para calcular las anualidades diferidas (consulte la Sección 12.1). La mayoría de las aplicaciones de perpetuidad requieren que calcule la inversión necesaria (\(PV_{ORD}\)o\(PV_{DUE}\)) o el pago (\(PMT\)). Utilice la sustitución algebraica y el reordenamiento cuando se requieran otras variables.
Notas Importantes
La calculadora BAII Plus se configura únicamente para anualidades a plazo fijo. Por lo tanto, no tiene una función o manera específica incorporada en la que entrar en una perpetuidad. Sin embargo, dado que una perpetuidad es una versión especializada de una anualidad regular, algunas adaptaciones menores a los insumos de anualidad permiten calcular perpetuidades. Ingrese todas las variables como de costumbre excepto los cambios que se muestran en la tabla a continuación.
| Variable | Resolviendo para\(PV_{ORD}\) o\(PV_{DUE}\) | Resolviendo para PMT |
|---|---|---|
| FV | \ (PV_ {ORD}\) o\(PV_{DUE}\) “>Asignar FV = 0 ya que el dinero en un futuro lejano no tiene valor hoy en día. | Asignar FV igual a PVORD o PVDUE, lo que se conozca. Recordemos que nunca se toca al director. |
| N | \ (PV_ {ORD}\) o\(PV_{DUE}\) “>Usa un valor grande como 10,000. * | Use un valor grande como 2,500. * |
* Esto colocará al FV lejos en un futuro lejano. Se podría utilizar un valor mayor, pero esto debe hacerse con precaución. Dependiendo de las cantidades que aparezcan en el cálculo de perpetuidad, la potencia resultante del exponente de un N muy grande puede superar las habilidades computacionales de la tecnología y producir un error. Si experimenta un error, intente bajar un poco el valor de\(N\).
Caminos hacia el éxito
Las fórmulas 12.5 y 12.6 representan versiones simplificadas de las fórmulas 11.4 y 11.5. Si estas nuevas fórmulas te parecen confusas, o si solo quieres recordar una sola fórmula para los valores actuales, puedes resolver cualquier pregunta de perpetuidad con las fórmulas del Capítulo 11. Si usa estas fórmulas, debe sustituir un valor extremadamente grande de N en la fórmula usando las sustituciones de tecnología discutidas en la tabla anterior.
- Si un solo pago se coloca hoy en una perpetuidad ordinaria, ¿su valor futuro será mayor, menor o igual?
- Si hoy se coloca una suma global en una perpetuidad debida, ¿su valor futuro será mayor, menor o igual?
- Responder
-
- Es lo mismo después de cada retiro de intereses y mayor entre retiros.
- Es lo mismo inmediatamente antes de cualquier retiro de intereses y siempre menor entre retiros. Recordemos que el primer pago se retira inmediatamente, lo que resulta en un principal que permanece menor que el monto original
Kendra es la directora de recursos humanos y quiere ofrecer un beneficio para nuevos empleados a través de un programa de becas corporativas. Cada año, se pondrán a disposición de los hijos de los empleados de la empresa 10 becas de $1,000. Si las primeras becas se van a ofrecer anualmente a partir de un año a partir de ahora, ¿qué monto se debe invertir hoy en 7.5% compuesto anualmente para financiar el programa de becas a perpetuidad?
Solución
Paso 1:
Calcular hoy una cantidad que debe invertirse de tal manera que pueda pagar los fondos necesarios al final de cada año a perpetuidad. Los intervalos de pago y capitalización son los mismos, por lo tanto se trata de una perpetuidad simple ordinaria. Determinar el valor presente (\(PV_{ORD}\)).
Lo que ya sabes
Paso 1 (continuación):
El cronograma para la perpetuidad aparece a continuación.

Paso 2:
\(IY\)= 7.5%,\(CY\) = 1,\(PMT\) = 10 × $1,000 = $10,000,\(PY\) = 1
Cómo Llegará
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
No es necesario para perpetuidades.
Paso 5:
Aplicar Fórmula 12.5.
Realizar
Paso 3:
\(i=7.5 \% / 1=7.5 \%\)
\[PV_{ORD}=\dfrac{\$ 10,000}{(1+0.075)^{\frac{1}{1}}-1}=\$ 133,333.33 \nonumber \]
Instrucciones de la calculadora
| Modo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| FINAL | 10000 | 7.5 | Respuesta: -133,333,3333 | 10000 | 0 | 1 | 1 |
Si Kendra hace que su compañía coloque $133,333.33 en la cuenta de perpetuidad, ganará intereses de 10,000 dólares al 7.5% compuesto anualmente cada año, lo que financiará el programa de becas a perpetuidad.
En memoria de su difunto padre, quien fue un gerente de marketing de gran éxito, a Brian le gustaría establecer un programa de becas de marketing con la escuela de negocios de su universidad. Él es capaz de donar 100.000 dólares del patrimonio de su padre para establecer el fondo. Si el fondo de perpetuidad puede ganar 6.3% compuesto semestralmente y la primera beca se va a proporcionar de inmediato, ¿qué monto anual de beca puede ofrecer el fondo?
Solución
Paso 1:
Calcular el monto del pago perpetuo que la contribución puede sostener. Los pagos y los intervalos de capitalización son diferentes, mientras que los pagos comienzan de inmediato. Por lo tanto, se trata de una perpetuidad general debida. Determinar el monto del pago de perpetuidad (PMT).
Lo que ya sabes
Paso 1 (continuación):
El cronograma de la beca aparece a continuación.

Paso 2:
\(IY\)= 6.3%,\(CY\) = 2,\(PV_{DUE}\) = $100,000,\(PY\) = 1
Cómo Llegará
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
No es necesario en perpetuidades.
Paso 5:
Sustituir a la Fórmula 12.6, reordenando para\(PMT\).
Realizar
Paso 3:
\(i=6.3 \% / 2=3.15 \% \)
Paso 5:
\[\$ 100,000=PMT\left(\dfrac{1}{(1+0.0315)^{\frac{2}{1}}-1}+1\right) \nonumber \]
\[\$ 100,000=PMT(16.626892) \nonumber \]
\[\$ 6,014.35=PMT \nonumber \]
Instrucciones de la calculadora
| Modo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 2500 | 6.3 | -100000 | Respuesta: 6,014,353018 | 100000 | 1 | 2 |
La donación de Brian permitirá una cantidad de beca inmediata de $6,014.35, que dejará $100,000 − $6,014.35 = $93,985.65 principal en la cuenta. Este monto principal podrá ganar $6,014.35 a perpetuidad cada año.
Uno de los métodos para valorar las acciones ordinarias es determinar el valor presente de sus dividendos futuros. Si se pronostica que IBM Corporation tendrá dividendos de cierre de año de $1.50 por acción para los próximos tres años seguidos de $1.80 por acción a perpetuidad, ¿cuánto debería estar dispuesto a pagar un inversionista si requiere una tasa de rendimiento trimestral compuesta del 12%?
Solución
Paso 1:
Hay diferentes capitalización y pagos, y los pagos se realizan al final del intervalo. Por lo tanto, se trata de una combinación de una anualidad general ordinaria para los tres primeros años seguida de una perpetuidad general ordinaria. Calcular el valor presente de las acciones ordinarias (\(PV_{ORD}\)).
Lo que ya sabes
Paso 1 (continuación):
El cronograma de las acciones ordinarias aparece a continuación.
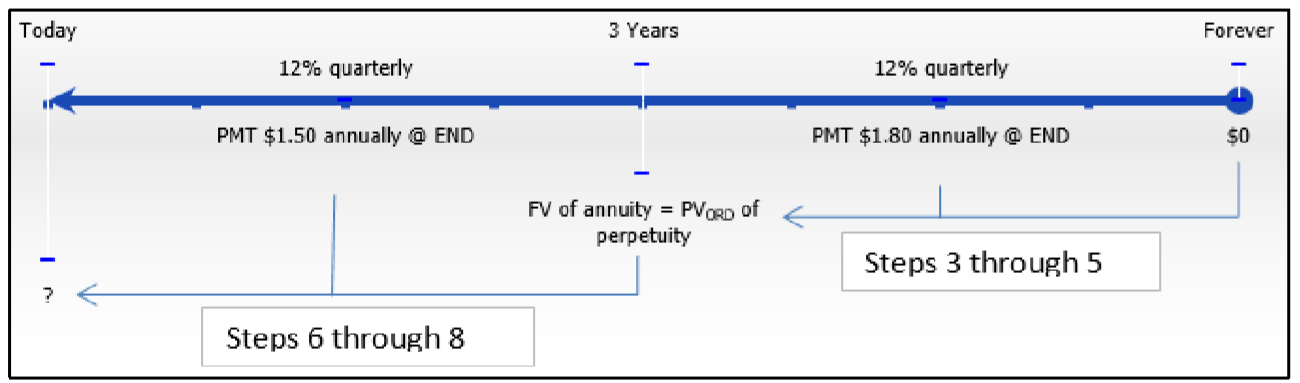
Paso 2:
Perpetuidad General Ordinaria:\(IY\)\(CY\) = 12%, = 4,\(PMT\) = $1.80,\(PY\) = 1
Cómo Llegará
A partir del lado derecho de la línea de tiempo, calcular primero el valor presente de la perpetuidad.
Paso 3:
Aplicar Fórmula 9.1.
Paso 4:
No es necesario en perpetuidades.
Paso 5:
Aplicar Fórmula 12.5. Después calcular el valor presente de la anualidad trienal.
Paso 6:
Aplicar las Fórmulas 9.2 y 9.5 (reordenando para\(PV\)) para encontrar el valor futuro pago único (que es el\(PV_{ORD}\) de la perpetuidad).
Paso 7:
Aplicar la Fórmula 11.1 y la Fórmula 11.4 a la anualidad.
Paso 8:
Suma los resultados del paso 6 y del paso 7 para obtener el valor de las acciones hoy mismo.
Realizar
Paso 3:
\(i=12 \% / 4=3 \%\)
Paso 5:
\[PV_{ORD}=\dfrac{\$ 1.80}{(1+0.03)^{\frac{4}{1}}-1}=\$ 14.341622 \nonumber \]
Paso 6:
\(N=4 \times 3=12 \text { compounds } \)
\[\$ 14.341622=PV(1+0.03)^{12} \nonumber \]
\[PV=\$ 14.341622 \div(1+0.03)^{12}=\$ 10.058925 \nonumber \]
Paso 7:
\(N=1 \times 3=3 \text { payments }\)
\[PV_{ORD }=\$ 1.50\left[\dfrac{1-\left[\frac{1}{(1+0.03)^{\frac{4}{1}}}\right]^{3}}{(1+0.03)^{\frac{4}{1}}-1}\right]=\$ 3.568914 \nonumber \]
Paso 8:
\[\$ 10.058925+\$ 3.568914=\$ 13.63 \nonumber \]
Instrucciones de la calculadora
| Pasos | Modo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| 3 - 5 | FINAL | 10000 | 12 | Respuesta: -14.341622 | 1.8 | 0 | 1 | 4 |
| 6 - 8 | \(\surd\) | 3 | \(\surd\) | Respuesta: -13.627839 | 1.5 | 14.341622 | \(\surd\) | \(\surd\) |
Si un inversionista desea una tasa de retorno del 12% sobre su inversión, estaría dispuesto a pagar 13.63 dólares por acción para recibir los dividendos a perpetuidad.


