1.5: Más aplicaciones
- Page ID
- 113614
En esta sección, aprenderás a:
- Resuelve un sistema lineal en dos variables.
- Encontrar el punto de equilibrio cuando se dan una ecuación de demanda y oferta.
- Encuentre el punto de equilibrio cuando se dan las funciones de ingresos y costos.
Encontrar el punto de intersección de dos líneas
En esta sección, haremos problemas de aplicación que involucren la intersección de líneas. Por lo tanto, antes de continuar, primero aprenderemos a encontrar la intersección de dos líneas.
Encuentra la intersección de la línea\(y = 3x -1\) y la línea\(y = - x + 7\).
Solución
Gráficamos ambas líneas en los mismos ejes, como se muestra a continuación, y leemos la solución (2, 5).
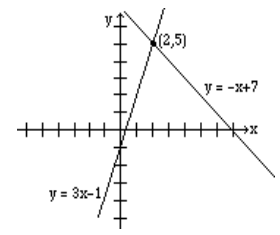
Encontrar gráficamente una intersección de dos líneas no siempre es fácil ni práctico; por lo tanto, ahora aprenderemos a resolver estos problemas algebraicamente.
En el punto donde dos líneas se cruzan, los\(y\) valores\(x\) y para ambas líneas son los mismos. Entonces, para encontrar la intersección, o bien dejamos que los\(x\) -valores o los\(y\) -valores sean iguales.
Si tuviéramos que resolver algebraicamente el ejemplo anterior, será más fácil dejar que los valores y sean iguales. Ya que\(y = 3x - 1\) para la primera línea, y\(y = - x + 7\) para la segunda línea, al dejar que los valores y sean iguales, obtenemos
\ begin {alineado}
3 x-1&=-x+7\\
4 x&=8\\
x&=2
\ end {alineado}
Al sustituir\(x = 2\) en cualquiera de las dos ecuaciones, obtenemos\(y = 5\).
De ahí, la solución (2, 5).
Un método algebraico común utilizado para resolver sistemas de ecuaciones se llama método de eliminación. El objetivo es eliminar una de las dos variables sumando los lados izquierdo y derecho de las ecuaciones juntos. Una vez que se elimina una variable, tenemos una ecuación con una sola variable para que se pueda resolver. Finalmente, al sustituir el valor de la variable que se ha encontrado en una de las ecuaciones originales, obtenemos el valor de la otra variable.
Encuentra la intersección de las líneas\(2x + y = 7\) y\(3x - y = 3\) por el método de eliminación.
Solución
Agregamos los lados izquierdo y derecho de las dos ecuaciones.
\ begin {alineado}
2 x+y&=7\\
3x-y&=3\\\ hline 5x&=10\\
x&=2
\ end {alineado}
Ahora sustituimos\(x = 2\) en cualquiera de las dos ecuaciones y resolvemos para\(y\).
\ begin {alineado}
2 (2) +y&=7\\
y&=3
\ end {alineado}
Por lo tanto, la solución es (2, 3).
Resolver el sistema de ecuaciones\(x + 2y = 3\) y\(2x + 3y = 4\) por el método de eliminación.
Solución
Si sumamos las dos ecuaciones, no se elimina ninguna de las variables. Pero la variable se\(x\) puede eliminar multiplicando la primera ecuación por -2, y dejando la segunda ecuación sin cambios.
\ begin {alineado}
-2 x-4 y &=-6\\
2 x+3 y &=4\
\ hline -y &=-2\\
y &=2
\ end {alineado}
Sustituyendo\(y = 2\) en\(x + 2y = 3\), obtenemos
\ begin {array} {l}
x+2 (2) =3\\
x=-1
\ end {array}
Por lo tanto, la solución es (-1, 2).
Resolver el sistema de ecuaciones\(3x - 4y = 5\) y\(4x - 5y = 6\).
Solución
Esta vez, multiplicamos la primera ecuación por - 4 y la segunda por 3 antes de sumar. (La elección de los números no es única.)
\ begin {alineado}
-12 x+16 y &=-20\\
12 x-15 y &=18\\ hline y&=-2
\ end {alineado}
Al sustituir y = - 2 en cualquiera de las ecuaciones, obtenemos x = -1.
De ahí que la solución sea (-1, -2).
LA OFERTA, LA DEMANDA Y EL EQUILIBRIO DEL PRECIO DE MERCADO
En una economía de libre mercado la curva de oferta para un producto básico es el número de artículos de un producto que pueden estar disponibles a diferentes precios, y la curva de demanda es el número de artículos que el consumidor comprará a diferentes precios.
A medida que aumenta el precio de un producto, su demanda disminuye y la oferta aumenta. Por otro lado, a medida que el precio disminuye la demanda aumenta y la oferta disminuye. El precio de equilibrio se alcanza cuando la demanda es igual a la oferta.
La curva de oferta para un producto es\(y = 3.5x - 14\) y la curva de demanda para el mismo producto es\(y = - 2.5x + 34\), donde x es el precio e y el número de artículos producidos. Encuentra lo siguiente.
- ¿Cuántos artículos se suministrarán a un precio de $10?
- ¿Cuántos artículos se demandarán a un precio de $10?
- Determinar el precio de equilibrio.
- ¿Cuántos artículos se producirán al precio de equilibrio?
Solución
a) Sustituimos\(x = 10\) en la ecuación de oferta,\(y = 3.5x - 14\); la respuesta es\(y = 3.5(10) - 14 =21\).
b) Sustituimos\(x = 10\) en la ecuación de demanda,\(y = - 2.5x + 34\); la respuesta es\(y = - 2.5(10) + 34= 9\).
c) Al dejar que la oferta iguale a la demanda, obtenemos
\ begin {alineado}
3.5x-140 &=-25x+340\\
6x &=480\\
x &=\ $8
\ end {alineado}
d) Sustituimos ya sea\(x = 8\) en la ecuación de oferta o demanda; obtenemos\(y = 14\).
La gráfica muestra la intersección de las funciones de oferta y demanda y su punto de intersección, (8,140).
Interpretación: En equilibrio, el precio es de $8 por artículo, y 140 artículos son producidos por los proveedores y comprados por los consumidores.
El punto de equilibrio
En un negocio, el beneficio se genera mediante la venta de productos.
- Si una empresa vende x número de artículos a un precio P, entonces el ingreso R es el precio multiplicado por el número de artículos vendidos:\(R = P \cdot x\).
- Los costos de producción C son la suma de los costos variables y los costos fijos, y a menudo se escriben como C = mx + b, donde x es el número de artículos fabricados.
-
- La pendiente m es el llamado costo marginal y representa el costo para producir un artículo o unidad adicional.
- El costo variable, mx, depende de cuánto se esté produciendo
- El costo fijo b es constante; no cambia por mucho que se produzca.
- La ganancia es igual a Ingresos menos Costo: Beneficio = R − C
Una empresa obtiene ganancias si los ingresos son mayores que el costo. Hay una pérdida si el costo es mayor que los ingresos. El punto en la gráfica donde los ingresos son iguales al costo se llama punto de equilibrio. En el punto de equilibrio, la ganancia es 0.
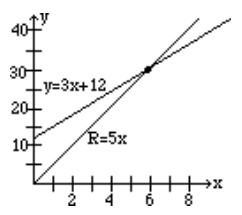
Si la función de ingresos de un producto es\(R = 5x\) y la función de costo es\(y = 3x + 12\), encuentre lo siguiente.
- Si se producen 4 artículos, ¿cuáles serán los ingresos?
- ¿Cuál es el costo de producir 4 artículos?
- ¿Cuántos artículos se deben producir para alcanzar el punto de equilibrio?
- ¿Cuáles serán los ingresos y el costo en el punto de equilibrio?
Solución
a) Sustituimos\(x = 4\) en la ecuación de ingresos\(R = 5x\), y la respuesta es\(R = 20\).
b) Sustituimos\(x = 4\) en la ecuación de costo\(C = 3x + 12\), y la respuesta es\(C = 24\).
c) Al dejar que los ingresos sean iguales al costo, obtenemos
\ begin {alineado}
5x&=3x+12\\
x&=6\\
\ end {alineado}
d) Sustituir ya sea\(x = 6\) en la ecuación de ingresos o costo: obtenemos\(R = C = 30\).
La gráfica siguiente muestra la intersección de las funciones de ingresos y costos y su punto de intersección, (6, 30).