3.2: Aplicaciones de minimización
- Page ID
- 113918
En esta sección, aprenderás a:
- Formular problemas de programación lineal de minimización
- Gráfico de regiones de viabilidad para problemas de programación lineal de maximización
- Determinar soluciones óptimas para problemas de programación lineal de maximización.
Los problemas de programación lineal de minimización se resuelven de la misma manera que los problemas de maximización.
Para el programa lineal de minimización estándar, las restricciones son de la forma\(ax + by ≥ c\), a diferencia de la forma\(ax + by ≤ c\) para el problema de maximización estándar. Como resultado, la solución factible se extiende indefinidamente a la parte superior derecha del primer cuadrante, y no tiene límites. Pero eso no es una preocupación, ya que para minimizar la función objetiva, la línea asociada a la función objetiva se mueve hacia el origen, y el punto crítico que minimiza la función está más cerca del origen.
Sin embargo, se debe tener en cuenta que en el caso de una región de factibilidad no delimitada, existe la posibilidad de que no exista una solución óptima.
En una universidad, el profesor Symons desea emplear a dos personas, John y Mary, para calificar trabajos para sus clases. John es un estudiante graduado y puede calificar 20 trabajos por hora; John gana $15 por hora por calificar trabajos. Mary es asociada postdoctoral y puede calificar 30 trabajos por hora; Mary gana $25 por hora por calificar trabajos. Cada uno debe ser empleado al menos una hora a la semana para justificar su empleo.
Si el Prof. Symons tiene al menos 110 trabajos para calificar cada semana, ¿cuántas horas semanales debe emplear a cada persona para minimizar el costo?
Solución
Elegimos las variables de la siguiente manera:
Let\(x\) = El número de horas por semana John está empleado.
y\(y\) = El número de horas semanales Mary está empleada.
La función objetiva es
\[C = 15x + 25y \nonumber \]
El hecho de que cada uno deba trabajar al menos una hora cada semana da como resultado las siguientes dos restricciones:
\ [\ begin {array} {l}
x\ geq 1\\
y\ geq 1
\ end {array}\ nonumber\]
Dado que John puede calificar 20 trabajos por hora y Mary 30 papeles por hora, y hay al menos 110 trabajos para calificar por semana, obtenemos
\[20x + 30y ≥ 110 \nonumber \]
El hecho de que\(x\) y no\(y\) sean negativos, obtenemos
\[x ≥ 0 \text{, and } y ≥ 0. \nonumber \]
El problema se ha formulado de la siguiente manera.
\ [\ begin {array} {ll}
\ textbf {Minimizar} &\ mathrm {C} =15\ mathrm {x} +25\ mathrm {y}\
\\ textbf {Sujeto a:} &\ mathrm {x}\ geq 1\\
&\ mathrm {y}\ geq 1\\
& 20\ mathrm {x} +30\ mathrm {y}\ 110\\
&\ mathrm {x}\ geq 0; \ mathrm {y}\ geq 0
\ end {array}\ nonumber\]
Para resolver el problema, graficamos las restricciones de la siguiente manera:
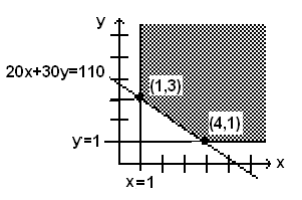
Nuevamente, hemos sombreado la región de factibilidad, donde se satisfacen todas las limitaciones.
Si usamos punto de prueba (0,0) que no se encuentra en ninguna de las restricciones, observamos que (0, 0) no satisface ninguna de las restricciones\(x ≥ 1\),\(y ≥ 1\),\(20x + 30y ≥ 110\). Así, todo el sombreado para la región de factibilidad se encuentra en el lado opuesto de las líneas de restricción desde el punto (0,0).
Alternativamente podríamos usar el punto de prueba (4,6), que tampoco se encuentra en ninguna de las líneas de restricción. Encontramos que (4,6) satisface todas las restricciones de desigualdad. En consecuencia, todo el sombreado para la región de factibilidad se encuentra en el mismo lado de las líneas de restricción que el punto (4,6).
Dado que el valor extremo de la función objetiva siempre tiene lugar en los vértices de la región de factibilidad, identificamos los dos puntos críticos, (1, 3) y (4, 1). Para minimizar el costo, sustituiremos estos puntos en la función objetiva para ver qué punto nos da el costo mínimo cada semana. Los resultados se enumeran a continuación.
| Puntos críticos | Ingresos |
| (1, 3) | 15 (1) + 25 (3) = $90 |
| (4, 1) | 15 (4) + 25 (1) = $85 |
El punto (4, 1) da el menor costo, y ese costo es de $85. Por lo tanto, concluimos que para minimizar los costos de calificación, el profesor Symons debe emplear a John 4 horas a la semana, y Mary 1 hora a la semana a un costo de $85 por semana.
El profesor Hamer sigue una dieta baja en colesterol. Durante el almuerzo en la cafetería de la universidad, siempre elige entre dos comidas, Pasta o Tofu. La siguiente tabla enumera la cantidad de proteínas, carbohidratos y vitaminas que proporciona cada comida junto con la cantidad de colesterol que está tratando de minimizar. El señor Hamer necesita al menos 200 gramos de proteína, 960 gramos de carbohidratos y 40 gramos de vitaminas para el almuerzo cada mes. En este periodo de tiempo, ¿cuántos días debe tener la comida de Pasta, y cuántos días la comida de Tofu para que obtenga la cantidad adecuada de proteínas, carbohidratos y vitaminas y al mismo tiempo minimice su ingesta de colesterol?
| PASTA | TOFU | |
| PROTEÍNA | 8g | 16g |
| HIDRATOS DE CARBONO | 60g | 40g |
| VITAMINA C | 2g | 2g |
| COLESTEROL | 60mg | 50mg |
Solución
Elegimos las variables de la siguiente manera.
Let\(x\) = El número de días que el señor Hamer come Pasta.
y\(y\) = El número de días que el señor Hamer come Tofu.
Dado que está tratando de minimizar su ingesta de colesterol, nuestra función objetiva representa la cantidad total de colesterol C proporcionada por ambas comidas.
\[C = 60x + 50y \nonumber \]
La restricción asociada con la cantidad total de proteína proporcionada por ambas comidas es
\[8x + 16y ≥ 200 \nonumber \]
De igual manera, se obtienen las dos limitaciones asociadas a la cantidad total de carbohidratos y vitaminas, y son
\ [\ begin {array} {l}
60 x+40 y\ geq 960\\
2 x+2 y\ geq 40
\ end {array}\ nonumber\]
Las restricciones que indican que x e y no son negativas son
\[x ≥ 0 \text{, and } y ≥ 0 \nonumber. \nonumber \]
Resumimos toda la información de la siguiente manera:
\ [\ begin {array} {ll}
\ textbf {Minimizar} &\ mathrm {C} =60\ mathrm {x} +50\ mathrm {y}\
\\ textbf {Sujeto a:} & 8\ mathrm {x} +16\ mathrm {y}\ geq 200\\
& 60\ mathrm {x} +40\ mathrm {y}\ geq\ 960\
& 2\ mathrm {x} +2\ mathrm {y}\ geq 40\\
&\ mathrm {x}\ geq 0;\ mathrm {y}\ geq 0
\ end {array}\ nonumber\]
Para resolver el problema, graficamos las restricciones y sombreamos la región de factibilidad.
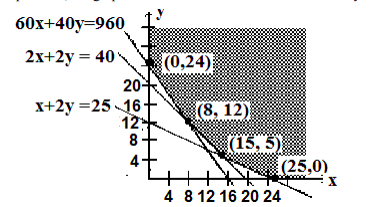
Hemos sombreado la región de factibilidad sin límites, donde se satisfacen todas las limitaciones.
Para minimizar la función objetiva, encontramos los vértices de la región de factibilidad. Estos vértices son (0, 24), (8, 12), (15, 5) y (25, 0). Para minimizar el colesterol, sustituiremos estos puntos en la función objetiva para ver qué punto nos da el menor valor. Los resultados se enumeran a continuación.
| Puntos críticos | Ingresos |
| (0, 24) | 60 (0) + 50 (24) = 1200 |
| (8, 12) | 60 (8) + 50 (12) = 1080 |
| (15, 5) | 60 (15) + 50 (5) = 1150 |
| (25, 0) | 60 (25) + 50 (0) = 1500 |
El punto (8, 12) da la menor cantidad de colesterol, que es de 1080 mg. Esto establece que por cada 20 comidas, el profesor Hamer debe comer Pasta 8 días, y Tofu 12 días.
Debemos ser conscientes de que en algunos casos, un programa lineal puede no tener una solución óptima.
- Un programa lineal puede no tener una solución óptima si no hay una región de factibilidad. Si las restricciones de desigualdad no son compatibles, puede que no haya una región en la gráfica que satisfaga todas las restricciones. Si el programa lineal no tiene una solución factible que satisfaga todas las restricciones, entonces no puede tener una solución óptima.
- Un programa lineal puede no tener una solución óptima si la región de factibilidad no tiene límites.
- Los dos programas lineales de minimización que examinamos tenían regiones de factibilidad sin límites. La región de factibilidad estaba limitada por restricciones en algunos lados, pero no estaba completamente encerrada por las limitaciones. Ambos problemas de minimización tuvieron soluciones óptimas.
- Sin embargo, si consideráramos un problema de maximización con una región de factibilidad no acotada similar, el programa lineal no tendría una solución óptima. No importa qué valores de x e y se seleccionaron, siempre podríamos encontrar otros valores de\(x\) y\(y\) que producirían un mayor valor para la función objetiva. En otras palabras, si el valor de la función objetivo puede aumentarse sin límite en un programa lineal con una región factible no acotada, no existe una solución máxima óptima.
Si bien el método de resolución de problemas de minimización es similar al de los problemas de maximización, aún sentimos que debemos resumir los pasos involucrados.
Minimización de problemas de programación lineal
- Escribe la función objetiva.
- Escribe las restricciones.
- Para problemas de programación lineal de minimización estándar, las restricciones son de la forma:\(ax + by ≥ c\)
- Dado que las variables no son negativas, incluyen las restricciones:\(x ≥ 0\);\(y ≥ 0\).
- Grafica las restricciones.
- Sombra la región de factibilidad.
- Encuentra los puntos de esquina.
- Determinar el punto de esquina que da el valor mínimo.
- Esto se puede hacer encontrando el valor de la función objetiva en cada punto de esquina.
- Esto también se puede hacer moviendo la línea asociada a la función objetiva.
- Existe la posibilidad de que el problema no tenga solución


