5.3: Gráficas y Propiedades de las Funciones de Crecimiento Exponencial y Decaimiento
- Page ID
- 113698
En esta sección, usted:
- Examinar las propiedades de las funciones exponenciales
- Examinar gráficos de funciones exponenciales
Una función exponencial se puede escribir en formas
\[f(x) = ab^x = a(1 + r)^x = ae^{kx} \nonumber \]
donde
- \(\mathbf{a}\)es el valor inicial porque\(f(0) = a\). En los modelos de crecimiento y decaimiento que examinamos en este libro de texto finito de matemáticas,\(a > 0\).
- \(\mathbf{b}\)a menudo se llama el factor de crecimiento. Nos restringimos\(b\) a ser positivos (\(b > 0\)) porque incluso las raíces de los números negativos son indefinidas. Queremos que la función se defina para todos los valores de\(x\), pero\(b^x\) sería indefinida para algunos valores de\(x\) if\(b<0\).
- \(\mathbf{r}\)se llama tasa de crecimiento o decaimiento. En la fórmula para las funciones, usamos r en forma decimal, pero en el contexto de un problema solemos declarar r como un porcentaje.
- \(\mathbf{k}\)se llama tasa de crecimiento continuo o tasa de decaimiento continuo.
Propiedades de las Funciones de Crecimiento Exponencial
La función\(y=f(x) = ab^x\) representa el crecimiento si\(b > 1\) y\(a > 0\).
La tasa de crecimiento\(r\) es positiva cuando\(b>1\). Porque\(b = 1+ r > 1\), entonces\(r = b−1 > 0\)
La función\(y=f(x) = ae^{kx}\) representa el crecimiento si\(k > 0\) y\(a > 0\).
La función es una función creciente;\(y\) aumenta a medida que\(x\) aumenta.
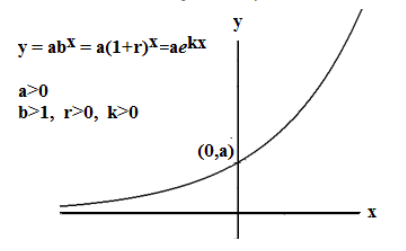
- Dominio: {todos los números reales}; todos los números reales se pueden ingresar a una función exponencial
- Rango: Si\(a>0\), el rango es {números reales positivos} La gráfica siempre está por encima del eje x.
- Asíntota horizontal: cuando\(b > 1\), la asíntota horizontal es el eje x negativo, ya que x se vuelve grande negativo. Usando notación matemática: como x → −∞, luego y → 0.
- La intercepción vertical es el punto\((0,a)\) en el eje y. No hay intercepción horizontal porque la función no cruza el eje x.
Propiedades de las funciones de decaimiento exponencial
La función\(y=f(x) = ab^x\) función representa decaimiento si\(0 < b < 1\) y\(a > 0\).
La tasa de crecimiento\(r\) es negativa cuando\(0 < b < 0\). Porque\(b=1+r < 1\), entonces\(r=b-1<0\).
La función\(y=f(x) = ae^{kx}\) función representa decaimiento si\(k < 0\) y\(a > 0\).
La función es una función decreciente;\(y\) disminuye a medida que\(x\) aumenta.
Dominio: {todos los números reales}; todos los números reales pueden ser introducidos en una función exponencial
Rango: Si\(a>0\), el rango es {números reales positivos} La gráfica siempre está por encima del eje x.
Asíntota horizontal: cuando\(b < 1\), la asíntota horizontal es el eje x positivo ya que x se vuelve grande positivo. Usando notación matemática: como x → ∞, luego y → 0.
La intercepción vertical es el punto\((0,a)\) en el eje y. No hay intercepción horizontal porque la función no cruza el eje x.
Las gráficas para las funciones de crecimiento exponencial y decaimiento se muestran a continuación para comparar.
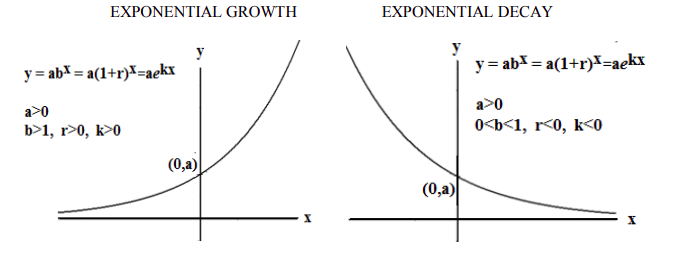
Una función exponencial es una función uno a uno
Observe que en la gráfica de una función exponencial, cada valor y en la gráfica ocurre solo una vez. Por lo tanto, cada valor y en el rango corresponde a solo un valor x. Entonces, para cualquier valor particular de y, puede usar la gráfica para ver qué valor de x es la entrada para producir ese valor y como salida. Esta propiedad se llama “uno a uno”.
Porque para cada valor de la salida y, se puede determinar de manera única el valor de la entrada x correspondiente, así cada función exponencial tiene una función inversa. La función inversa de una función exponencial es una función logarítmica, que investigaremos en la siguiente sección.
\(x\)años después del año 2015, la población de la ciudad de Fulton viene dada por la función\(y= f(x) = 35000(1.03^x)\). \(x\)años después del año 2015, la población de la ciudad de Greenville viene dada por la función\(y = g(x) = 80000(0.95^x)\). Compara las gráficas de estas funciones.
Solución
Los gráficos a continuación se crearon utilizando software de gráficos por computadora. También puedes graficar estas funciones usando una calculadora gráfica.
| Población de Fulton | Población de Greenville |
|---|---|
| \[y=f(x)=35000\left(1.03^{x}\right) \nonumber \] | \[y=g(x)=80000\left(0.95^{x}\right) \nonumber \] |
|
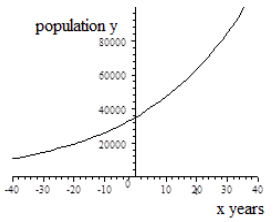
La población de Fulton va en aumento. \(b = 1.03 > 1\)y\(r=0.03>0\) Crecimiento Exponencial |
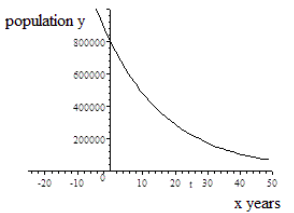
La población de Greenville está disminuyendo. \(b = 0.95 < 1\)y\(r = −0.05 < 0\) Decaimiento exponencial |
 |
 |
|
intercepción en Y: (0, 35000) La población inicial en 2015 es de 35000. |
intercepción en Y: (0,80000) La población inicial en 2015 es de 80000. |
| Asíntota horizontal: El eje x negativo es la asíntota horizontal. y → 0 como x → − ∞ | Asíntota horizontal: El eje x positivo es la asíntota horizontal. y → 0 como x → ∞ |
Dominio: En general, el dominio de ambas funciones\(y= f(x) = 35000(1.03^x)\) y\(y= g(x) = 80000(0.95^x)\) es el conjunto de todos los números reales.
Rango: El rango de ambas funciones es el conjunto de números reales positivos. Ambas gráficas siempre se encuentran por encima del eje x.
Dominio y Rango en el contexto de este problema:
Las funciones representan el tamaño de la población en función del tiempo posterior al año 2015. Restringiremos el dominio en este contexto, utilizando el “dominio práctico” como conjunto de todos los números reales no negativos:\(x≥0\). Entonces consideraríamos sólo la porción de la gráfica que se encuentra en el primer cuadrante.
- Si restringimos el dominio a\(x≥0\) para la función de crecimiento\(y= f(x) = 35000(1.03^x)\), entonces el rango para la población de Fulton es\(y ≥ 35,000\)
- Si restringimos el dominio a\(x≥0\) para la función de decaimiento\(y= g(x) = 80000(0.95^x)\), entonces el rango para la población de Greenville es\(y ≤ 80,000\).