6.4: Valor Presente de una Anualidad y Pago a Plazos
- Page ID
- 113590
En esta sección, aprenderás a:
- Encontrar el valor presente de una anualidad.
- Encuentra el monto del pago a plazos de un préstamo.
VALOR PRESENTE DE UNA ANUALIDAD
En la Sección 6.2 aprendimos a encontrar el valor futuro de una suma global, y en la Sección 6.3, aprendimos a encontrar el valor futuro de una anualidad. Con estos dos conceptos en la mano, ahora aprenderemos a amortizar un préstamo, y a encontrar el valor presente de una anualidad.
El valor presente de una anualidad es la cantidad de dinero que necesitaríamos ahora para poder realizar los pagos en la anualidad en el futuro. En otras palabras, el valor presente es el valor ahora de un flujo futuro de pagos.
Comenzamos por desglosar esto paso a paso para entender el concepto del valor presente de una anualidad. Después de eso, los ejemplos proporcionan una manera más eficiente de hacer los cálculos al trabajar con conceptos y cálculos que ya hemos explorado en las Secciones 6.2 y 6.3.
Supongamos que Carlos es dueño de una pequeña empresa y emplea a un subgerente para que lo ayude a administrar el negocio. Supongamos que ahora es el 1 de enero. Carlos planea pagar a su subgerente un bono de $1000 al final de este año y otro bono de $1000 al final del año siguiente. El negocio de Carlos tuvo buenas ganancias este año por lo que ahora quiere poner el dinero para los futuros bonos de su asistente en una cuenta de ahorro. El dinero que ponga ahora ganará intereses a una tasa de 4% anual compuesta anualmente mientras esté en la cuenta de ahorro.
¿Cuánto dinero debería poner Carlos en la cuenta de ahorro ahora para que pueda retirar 1000 dólares dentro de un año y otros 1000 en dos años?
Al principio, esto suena como un fondo de hundimiento. Pero es diferente. En un fondo de hundimiento, ponemos dinero en el fondo con pagos periódicos para ahorrar para acumular a una suma global especificada que es el valor futuro al final de un periodo de tiempo determinado.
En este caso queremos poner una suma global en la cuenta de ahorro ahora, para que esa suma global sea nuestro principal,\(\mathrm{P}\). Entonces queremos retirar esa cantidad como una serie de pagos de periodo; en este caso los retiros son una anualidad con pagos de $1000 al término de cada uno de dos años.
Tenemos que determinar el monto que necesitamos en la cuenta ahora, el valor presente, para poder hacer retirar los pagos periódicos posteriormente.
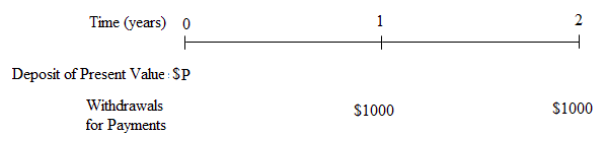
Utilizamos la fórmula de interés compuesto de la Sección 6.2 con\(r\) = 0.04 y\(n\) = 1 para la capitalización anual para determinar el valor presente de cada pago de $1000.
Considera el primer pago de $1000 al cierre del año 1. Que P 1 sea su valor presente
\[\$ 1000=P_{1}(1.04)^{1} \text { so } P_{1}=\$ 961.54 \nonumber \]
Ahora considere el segundo pago de $1000 al cierre del año 2. Let P 2 es su valor actual
\[\$ 1000=P_{2}(1.04)^{2} \text { so } P_{2}=\$ 924.56 \nonumber \]
Para realizar los pagos de $1000 en los horarios especificados en el futuro, la cantidad que Carlos necesita depositar ahora es el valor presente\(P=P_{1}+P_{2}=\$ 961.54+\$ 924.56=\$ 1886.10\)
El cálculo anterior fue útil para ilustrar el significado del valor presente de una anualidad.
Pero no es una forma eficiente de calcular el valor presente. Si tuviéramos una gran cantidad de pagos de anualidades, el cálculo paso a paso sería largo y tedioso.
Ejemplo\(\PageIndex{1}\) investiga y desarrolla una manera eficiente de calcular el valor presente de una anualidad, relacionando el valor futuro (acumulado) de una anualidad y su valor presente.
Supongamos que ha ganado una lotería que paga $1,000 mensuales durante los próximos 20 años. Pero, prefieres tener el monto total ahora. Si la tasa de interés es del 8%, ¿cuánto aceptará?
Solución
Este clásico problema de valor presente necesita de nuestra atención completa porque la racionalización que utilizamos para resolver este problema será utilizada nuevamente en los problemas a seguir.Considerar, a efectos de argumento, que dos personas el señor Cash y el Sr. Credit han ganado la misma lotería de $1,000 mensuales durante los próximos 20 años. Mr. Credit está contento con su pago mensual de $1,000, pero Mr. Cash quiere tener el monto completo ahora.
Nuestro trabajo es determinar cuánto debe obtener Mr. Cash. Razonamos de la siguiente manera:
Si Mr. Cash acepta P dólares, entonces los P dólares depositados en 8% por 20 años deberían arrojar la misma cantidad que los pagos mensuales de $1,000 por 20 años. Es decir, estamos comparando los valores futuros tanto para Mr. Cash como para Mr. Credit, y nos gustaría que los valores futuros fueran iguales.
Dado que el Sr. Cash está recibiendo una suma global de\(x\) dólares, su valor futuro viene dado por la fórmula de suma global que estudiamos en la Sección 6.2, y es
\[\mathrm{A}=\mathrm{P}(1+.08 / 12)^{240} \nonumber \]
Dado que el Sr. Crédito está recibiendo una secuencia de pagos, o una anualidad, de $1,000 mensuales, su valor futuro viene dado por la fórmula de anualidad que aprendimos en la Sección 6.3. Este valor es
\[\mathrm{A}=\frac{\$ 1000\left[(1+.08 / 12)^{240}-1\right]}{.08 / 12} \nonumber \]
La única forma en que Mr. Cash aceptará la cantidad que recibe es si estos dos valores futuros son iguales. Entonces los pusimos iguales y resolvemos por lo desconocido.
\ [\ begin {array} {l}
\ mathrm {P} (1+.08/12) ^ {240} =\ frac {\ $1000\ left [(1+.08/12) ^ {240} -1\ derecha]} {.08/12}\\ mathrm {P} (4.9268) =
\ $1000 (589.02041)\\ mathrm {P} (4.9268) =\ $1000 (589.02041)\
\ mathrm {P} (4.9268) =\\ mathrm {P} (268) =
\ $589020.41\\ mathrm {P} =\ $119,554.36
\ end {array}\ nonumber\]
El valor actual de una anualidad ordinaria de $1,000 mensuales por 20 años al 8% es de $119,554.36
El lector también debe señalar que si Mr. Cash toma su suma global de\(\mathrm{P}\) = 119,554.36 dólares y la invierte al 8% compuesto mensual, tendrá un valor acumulado de\(\mathrm{A}\) =$589,020.41 en 20 años.
PAGO A PLAZOS DE UN PRÉSTAMO
Si una persona o empresa necesita comprar o pagar algo ahora (un automóvil, una casa, colegiatura universitaria, equipo para un negocio) pero no tiene el dinero, puede pedir prestado el dinero como préstamo.
Reciben el monto del préstamo llamado principal (o valor presente) ahora y están obligados a devolver el principal en el futuro durante un período de tiempo establecido (plazo del préstamo), como pagos periódicos regulares con intereses.
Ejemplo\(\PageIndex{2}\) examina cómo calcular el pago del préstamo, utilizando razonamientos similares a Ejemplo\(\PageIndex{1}\).
Encuentra el pago mensual de un auto con un costo de $15,000 si el préstamo se amortiza a lo largo de cinco años a una tasa de interés del 9%.
Solución
De nuevo, considere el siguiente escenario:Dos personas, Mr. Cash y Mr. Credit, van a comprar el mismo auto que cuesta $15,000. El señor Cash paga en efectivo y se va, pero Mr. Credit quiere hacer pagos mensuales por cinco años.
Nuestro trabajo es determinar el monto del pago mensual. Razonamos de la siguiente manera:
Si Mr. Credit paga m dólares mensuales, entonces el pago de m dólares depositado cada mes al 9% por 5 años debería arrojar la misma cantidad que la suma global de $15,000 depositada por 5 años.
Nuevamente, estamos comparando los valores futuros tanto para Mr. Cash como para Mr. Credit, y nos gustaría que fueran los mismos.
Dado que Mr. Cash está pagando una suma global de $15,000, su valor futuro viene dado por la fórmula de suma global, y es
\[\$ 15,000(1+.09 / 12)^{60} \nonumber \]
Mr. Credit desea hacer una secuencia de pagos, o una anualidad, de\(x\) dólares mensuales, y su valor futuro viene dado por la fórmula de anualidad, y este valor es
\[\frac{\mathrm{x}\left[(1+.09 / 12)^{60}-1\right]}{.09 / 12} \nonumber \]
Fijamos las dos cantidades futuras iguales y resolvemos para lo desconocido.
\ [\ begin {array} {l}
\ $15,000 (1+.09/12) ^ {60} =\ frac {m\ left [(1+.09/12) ^ {60} -1\ right]} {.09/12}\\
\ $15,000 (1.5657) =m (75.4241)\\
\ $ 311.38=m
\ end {array}\ nonumber\]
Por lo tanto, el pago mensual necesario para reembolsar el préstamo es de $311.38 por cinco años.
RESUMEN DE LA SECCIÓN 6.4
Resumimos el método utilizado en los ejemplos\(\PageIndex{1}\) y\(\PageIndex{2}\) a continuación.
La Ecuación para Encontrar el Valor Presente de una Anualidad,
O el Pago a Plazos para un Préstamo
Si un pago de\(m\) dólares se realiza en una cuenta\(n\) veces al año a un interés\(r\), entonces el valor presente\(\mathrm{P}\) de la anualidad después de\(t\) años es
\[\mathbf{P}(\mathbf{1}+\mathbf{r} / \mathbf{n})^{\mathbf{n} \mathbf{t}}=\frac{\mathbf{m}\left[(\mathbf{1}+\mathbf{r} / \mathbf{n})^{\mathbf{n} \mathbf{t}}-\mathbf{1}\right]}{\mathbf{r} / \mathbf{n}} \nonumber \]
Cuando se utiliza para un préstamo, el monto\(\mathrm{P}\) es el monto del préstamo, y\(m\) es el pago periódico necesario para reembolsar el préstamo a lo largo de un plazo de\(t\) años con\(n\) pagos por año.
Si se necesita el valor actual o monto del préstamo, resuelva para\(P\)
Si se necesita el pago periódico, resuelva para\(m\).
Tenga en cuenta que la fórmula asume que el período de pago es el mismo que el período compuesto. Si estos no son lo mismo, entonces esta fórmula no aplica.
Por último, observamos que muchos libros finitos de matemáticas y finanzas desarrollan la fórmula para el valor presente de una anualidad de manera diferente.
En lugar de usar la fórmula:
\[\mathrm{P}(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}=\frac{\mathrm{m}\left[(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}-1\right]}{\mathrm{r} / \mathrm{n}} \label{6.4.1} \]
y resolviendo por el valor presente\(\mathrm{P}\) después de sustituir los valores numéricos por los otros ítems de la fórmula, muchos libros de texto primero resuelven la fórmula para para\(\mathrm{P}\) desarrollar una nueva fórmula para el valor presente. Entonces la información numérica puede ser sustituida en la fórmula de valor presente y evaluada, sin necesidad de resolver algebraicamente para\(\mathrm{P}\).
Método Alternativo para encontrar el Valor Presente de una Anualidad
Comenzando con la fórmula\ ref {6.4.1}:\(\mathrm{P}(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}=\frac{\mathrm{m}\left[(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}-1\right]}{\mathrm{r} / \mathrm{n}}\)
Divide ambos lados\((1+r / n)^{n t}\) para aislar\(\mathrm{P}\) y simplificar
\[P=\frac{m\left[(1+r / n)^{n t}-1\right]}{r / n} \cdot \frac{1}{(1+r / n)^{n t}} \nonumber \]
\[P=\frac{m\left[1-(1+r / n)^{-n t}\right]}{r / n} \label{6.4.2} \]
Los autores de este libro creen que es más fácil usar la fórmula\ ref {6.4.1} en la parte superior de esta página y resolver para\(\mathrm{P}\) o\(m\) según sea necesario. En este enfoque hay menos fórmulas para entender, y a muchos estudiantes les resulta más fácil aprender. En los problemas el resto de este capítulo, cuando un problema requiera el cálculo del valor presente de una anualidad, se utilizará la fórmula\ ref {6.4.1}.
Sin embargo, algunas personas prefieren la fórmula\ ref {6.4.2}, y es matemáticamente correcto usar ese método. Tenga en cuenta que si elige usar la fórmula\ ref {6.4.2}, debe tener cuidado con los exponentes negativos en la fórmula. Y si necesitabas encontrar el pago periódico, aún necesitarías hacer el álgebra para resolver por el valor de m.
Sería una buena idea consultar con su instructor para ver si tiene alguna preferencia. De hecho, normalmente puedes decir la preferencia de tu instructor señalando cómo explica y demuestra este tipo de problemas en clase.


