7.2: Diagramas de árboles y el axioma de multiplicación
- Page ID
- 113661
En esta sección aprenderás a
- Utilice árboles para contar posibles resultados en un proceso de varios pasos
- Utilice el axioma de multiplicación para contar posibles resultados en un proceso multi-stop.
En este capítulo, estamos tratando de desarrollar técnicas de conteo que serán utilizadas en el siguiente capítulo para estudiar la probabilidad. Una de las técnicas más fundamentales de este tipo es el llamado Axioma de Multiplicación. Antes de introducir el axioma de multiplicación, primero miramos algunos ejemplos.
Si una mujer tiene dos blusas y tres faldas, ¿cuántos atuendos diferentes que consisten en una blusa y una falda puede llevar?
Solución
Supongamos que llamamos a las blusas\(b_1\) y\(b_2\), y faldas\(s_1\),\(s_2\), y\(s_3\).
Podemos tener los siguientes seis atuendos.
\[b_1s_1, b_1s_2, b_1s_3, b_2s_1, b_2s_2, b_2s_3 \nonumber \]
Alternativamente, podemos dibujar un diagrama de árbol:
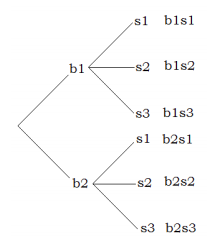
El diagrama de árbol nos da las seis posibilidades. El método implica dos pasos. Primero la mujer elige una blusa. Ella tiene dos opciones: blusa uno o blusa dos. Si elige blusa uno, tiene tres faldas para combinarla; falda uno, falda dos, o falda tres. De igual manera si elige blusa dos, puede emparejarla con cada una de las tres faldas, nuevamente. El diagrama de árbol nos ayuda a visualizar estas posibilidades.
El lector debe tener en cuenta que el proceso implica dos pasos. Para el primer paso de elegir una blusa, hay dos opciones, y para cada elección de blusa, hay tres opciones de elegir una falda. Entonces en conjunto hay\(2 \cdot 3 = 6\) posibilidades.
Si, en el ejemplo anterior, añadimos los zapatos al atuendo, tenemos el siguiente problema.
Si una mujer tiene dos blusas, tres faldas y dos zapatos de tacón, ¿cuántos atuendos diferentes que consisten en una blusa, una falda y un par de zapatos de tacón puede usar?
Solución
Supongamos que llamamos a las blusas\(b_1\) y\(b_2\), las faldas\(s_1\)\(s_2\),\(s_3\), y, y las bombas\(p_1\), y\(p_2\).
El siguiente diagrama de árbol resulta.
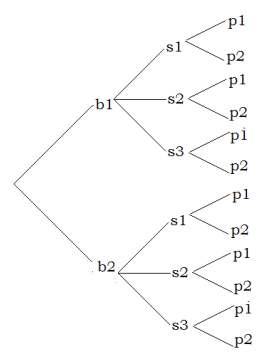
Contamos el número de ramas en el árbol, y vemos que hay 12 posibilidades diferentes.
Esta vez el método implica tres pasos. Primero, la mujer elige una blusa. Ella tiene dos opciones: blusa uno o blusa dos. Ahora supongamos que elige blusa uno. Esto nos lleva al paso dos del proceso que consiste en elegir una falda. Ella tiene tres opciones para una falda, y supongamos que elige la falda dos. Ahora que ha elegido una blusa y una falda, hemos pasado al tercer paso de elegir un par de zapatos de tacón. Como tiene dos pares de bombas, tiene dos opciones para el último paso. Supongamos que elige bombas dos. Ella ha elegido el atuendo que consiste en blusa uno, falda dos, y zapatos de tacón dos, o\(b_1s_2p_2\). Al mirar las diferentes ramas del árbol, uno puede ver fácilmente las otras posibilidades.
Lo importante a observar aquí, nuevamente, es que se trata de un proceso de tres pasos. Hay dos opciones para el primer paso de elegir una blusa. Para cada elección de blusa, hay tres opciones de elegir una falda, y para cada combinación de blusa y falda, hay dos opciones de seleccionar un par de zapatos de tacón.
Con todo, tenemos\(2 \cdot 3 \cdot 2 = 12\) diferentes posibilidades.
Los diagramas de árboles nos ayudan a visualizar las diferentes posibilidades, pero no son prácticas cuando las posibilidades son numerosas. Además, estamos mayormente interesados en encontrar el número de elementos en el conjunto y no la lista real de todas las posibilidades; una vez que se concibe el problema, podemos resolverlo sin un diagrama de árbol. Los dos ejemplos que acabamos de resolver pueden habernos dado una pista para hacer precisamente eso.
Tratemos ahora de resolver Ejemplo\(\PageIndex{2}\) sin diagrama de árbol. El problema consiste en tres pasos: elegir una blusa, elegir una falda y elegir un par de zapatos de tacón. El número de formas de elegir cada una se enumeran a continuación. Al multiplicar estos tres números obtenemos 12, que es lo que obtuvimos cuando hicimos el problema usando un diagrama de árbol.
| El número de formas de elegir una blusa | La cantidad de formas de elegir una falda | La cantidad de formas de elegir bombas |
| 2 | 3 | 2 |
El procedimiento que acabamos de emplear se llama axioma de multiplicación.
Si una tarea se puede hacer de\(m\) maneras, y una segunda tarea se puede hacer de\(n\) maneras, entonces la operación que involucra la primera tarea seguida de la segunda se puede realizar de\(m \cdot n\) maneras.
El axioma general de multiplicación no se limita a solo dos tareas y puede ser utilizado para cualquier número de tareas.
Una placa de camión consta de una letra seguida de cuatro dígitos. ¿Cuántas placas de este tipo son posibles?
Solución
Dado que hay 26 letras y 10 dígitos, tenemos las siguientes opciones para cada una.
| Carta | Dígito | Dígito | Dígito | Dígito |
| 26 | 10 | 10 | 10 | 10 |
Por lo tanto, el número de placas posibles es\(26 \cdot 10 \cdot 10 \cdot 10 \cdot 10=260,000\).
¿De cuántas maneras diferentes se puede responder una prueba de 3 preguntas verdadero-falso?
Solución
Como hay dos opciones para cada pregunta, tenemos
| Pregunta 1 | Pregunta 2 | Pregunta 3 |
| 2 | 2 | 2 |
Aplicando el axioma de multiplicación, obtenemos\(2 \cdot 2 \cdot 2 = 8\) diferentes formas.
Enumeramos las ocho posibilidades: TTT, TTF, TFT, TFF, FTT, FTF, FFT, FFF
El lector debe señalar que la primera letra en cada posibilidad es la respuesta correspondiente a la primera pregunta, la segunda letra corresponde a la respuesta a la segunda pregunta, y así sucesivamente. Por ejemplo, TFF, dice que la respuesta a la primera pregunta se da como verdadera, y las respuestas a la segunda y tercera preguntas son falsas.
¿De cuántas maneras diferentes pueden sentarse cuatro personas seguidas?
Solución
Supongamos que ponemos cuatro sillas seguidas, y procedemos a poner a cuatro personas en estos asientos.
Hay cuatro opciones para la primera silla que elegimos. Una vez que una persona se sienta en esa silla, sólo hay tres opciones para la segunda silla, y así sucesivamente. Enumeramos como se muestra a continuación.
| 4 | 3 | 2 | 1 |
Entonces, hay formas completamente\(4 \cdot 3 \cdot 2 \cdot 1 = 24\) diferentes.
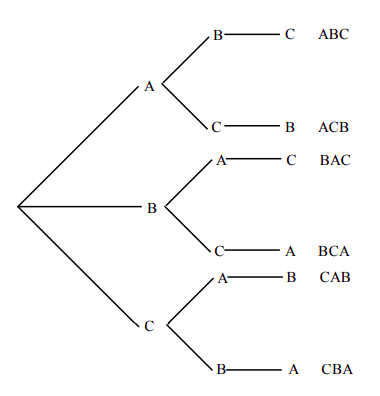
¿Cuántas secuencias de palabras de tres letras se pueden formar usando las letras {A, B, C} si no hay que repetir ninguna letra?
Solución
El problema es muy similar al ejemplo anterior.
Imagínese que un niño tiene tres bloques de construcción etiquetados A, B y C. Supongamos que pone estos bloques uno encima del otro para hacer secuencias de palabras. Para la primera letra tiene tres opciones, a saber, A, B o C. Supongamos que elige la primera letra para que sea una B, luego para el segundo bloque que debe ir encima de la primera, sólo tiene dos opciones: A o C. Y para la última letra sólo tiene una opción. A continuación enumeramos las opciones.
| 3 | 2 | 1 |
Por lo tanto, se pueden formar 6 secuencias de palabras diferentes.
Finalmente, nos gustaría ilustrar esto con un diagrama de árbol que muestra las seis posibilidades.