7.4: Permutaciones circulares y permutaciones con elementos similares
- Page ID
- 113673
En esta sección aprenderás a
- Contar el número de posibles permutaciones de elementos dispuestos en un círculo
- Contar el número de posibles permutaciones cuando hay elementos repetidos
En esta sección abordaremos los siguientes dos problemas.
- ¿De cuántas maneras diferentes pueden sentarse cinco personas en círculo?
- ¿De cuántas maneras diferentes se pueden arreglar las letras de la palabra MISSISSIS?
El primer problema entra en la categoría de Permutaciones Circulares, y el segundo bajo Permutaciones con Elementos Similares.
Permutaciones circulares
Supongamos que tenemos tres personas llamadas A, B y C. ¡Ya hemos determinado que pueden sentarse en línea recta en 3! o 6 maneras. Nuestro siguiente problema es ver de cuántas maneras estas personas pueden estar sentadas en círculo. Dibujamos un diagrama.
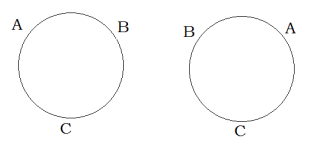
Ocurre que solo hay dos formas en las que podemos sentar a tres personas en círculo, relativas a las posiciones de la otra. Este tipo de permutación se llama permutación circular. En tales casos, no importa dónde se siente la primera persona, la permutación no se ve afectada. Cada persona puede cambiar tantos lugares como quiera, y la permutación no se cambiará. Nos interesa la posición de cada persona en relación con las demás. Imagínese a la gente en un tiovivo; la rotación de la permutación no genera una nueva permutación. Entonces en permutaciones circulares, la primera persona es considerada un lugaretero, y donde se sienta no importa.
El número de permutaciones de\(n\) elementos en un círculo es\((n-1)!\)
¿De cuántas maneras diferentes pueden sentarse cinco personas en una mesa circular?
Solución
Ya hemos determinado que la primera persona es sólo un lugaretero. Por lo tanto, solo hay una opción para el primer lugar. Tenemos
| 1 | 4 | 3 | 2 | 1 |
Entonces la respuesta es 24.
¿De cuántas maneras pueden sentarse cuatro parejas en una mesa redonda si los hombres y las mujeres quieren sentarse alternativamente?
Solución
De nuevo enfatizamos que la primera persona puede sentarse en cualquier lugar sin afectar la permutación.
Por lo que sólo hay una opción para el primer lugar. Supongamos que un hombre se sentó primero. La silla junto a ella debe pertenecer a una mujer, y hay 4 opciones. La siguiente silla pertenece a un hombre, por lo que hay tres opciones y así sucesivamente. A continuación enumeramos las opciones.
| 1 | 4 | 3 | 3 | 2 | 2 | 1 | 1 |
Entonces la respuesta es 144.
PERMUTACIONES CON ELEMENTOS SIMILARES
Determinemos el número de permutaciones distinguibles de las letras ELEMENTO.
Supongamos que hacemos diferentes todas las letras etiquetando las letras de la siguiente manera.
\[E_1LE_2ME_3NT \nonumber \]
Ya que todas las letras son ahora diferentes, ¡hay 7! diferentes permutaciones.
Veamos ahora una de esas permutaciones, digamos
\[LE_1ME_2NE_3T \nonumber \]
Supongamos que formamos nuevas permutaciones a partir de este arreglo solo moviendo las E. Claramente, ¡hay 3! o 6 de tales arreglos. Los enumeramos a continuación.
\ begin {alineado} &\ mathrm {LE} _ {1}\ mathrm {ME} _ {2}\ mathrm {NE} _ {3}\
&\ mathrm {LE} _ {1}\ mathrm {ME} _ {3}\ mathrm {NE} _ {2}\
&\ mathrm {LE} _ {2}\ mathrm {ME} _ {1}\ mathrm {ME} _ {1}\ mathrm rm {NE} _ {3}\ mathrm {T}\\
&\ mathrm {LE} _ {2}\ mathrm {ME} _ {3}\ mathrm {NE} _ {1}\ mathrm {T}\\
&\ mathrm {LE} _ {3}\ mathrm {ME} _ {2}\ mathrm {NE} _ {1}\ mathrm {T}\\
&\ mathrm {LE} _ {3}\ mathrm {ME} _ {I}\ mathrm {NE} _ {2}\ mathrm {T}\ end {alineado}
Debido a que las E no son diferentes, solo hay un arreglo LEMENET y no seis. Esto es cierto para cada permutación.
Supongamos que hay n diferentes permutaciones de las letras ELEMENTO.
Después hay\(n \cdot 3!\) permutaciones de las letras\(E_1LE_2ME_3NT\).
¡Pero sabemos que hay 7! permutaciones de las letras\(E_1LE_2ME_3NT\).
Por lo tanto,\(n \cdot 3! = 7!\)
O\(n = \frac{7!}{3!}\).
Esto nos da el método que estamos buscando.
El número de permutaciones de n elementos tomados\(n\) a la vez, con\(r_1\) elementos de un tipo,\(r_2\) elementos de otro tipo, y así sucesivamente, es
\[\frac{n !}{r_{1} ! r_{2} ! \ldots r_{k} !} \nonumber \]
Encuentra el número de diferentes permutaciones de las letras de la palabra MISSISSIS.
Solución
La palabra MISSISSIS tiene 11 letras. Si las letras fueran todas diferentes ¡habrían sido 11! diferentes permutaciones. Pero Mississippi tiene 4 S, 4 I y 2 P que son iguales.
Entonces la respuesta es\(\frac{11!}{4!4!2!} = 34,650\).
Si una moneda es arrojada seis veces, ¿cuántos resultados diferentes que consisten en 4 cabezas y 2 colas hay?
Solución
Nuevamente, tenemos permutaciones con elementos similares.
Estamos buscando permutaciones para las letras HHHHTT.
La respuesta es\(\frac{6!}{4!2!} = 15\).
¿De cuántas maneras diferentes se pueden disponer en fila 4 níqueles, 3 dimes y 2 cuartos?
Solución
Suponiendo que todas las monedas de cinco centavos son similares, todas las monedas de diez centavos son similares, y todos los cuartos son similares, tenemos permutaciones con elementos similares. Por lo tanto, la respuesta es
\[\frac{9 !}{4 ! 3 ! 2 !}=1260 \nonumber \]
Un corredor de bolsa quiere asignar 20 nuevos clientes por igual a 4 de sus vendedores. ¿De cuántas maneras diferentes se puede hacer esto?
Solución
Esto significa que cada vendedor recibe 5 clientes. El problema se puede considerar como un problema de particiones ordenadas. En ese caso, usando la fórmula obtenemos
\[\frac{20 !}{5 ! 5 ! 5 ! 5 !}=11,732,745,024 \nonumber \]
Un centro comercial tiene una fila recta de 5 mástiles en su plaza de entrada principal. Tiene 3 banderas verdes idénticas y 2 banderas amarillas idénticas. ¿Cuántos arreglos distintos de banderas en los mástiles son posibles?
Solución
El problema puede considerarse como distintas permutaciones de las letras GGGYY; es decir, arreglos de 5 letras, donde 3 letras son similares, y las 2 letras restantes son similares:
\[ \frac{5 !}{3 ! 2 !} = 10 \nonumber \]
Solo para proporcionar un poco más de información sobre la solución, enumeramos las 10 permutaciones distintas:
GGGYY, GGYGY, GGYYG, GYGGY, GYGYG, GYGYGG, YGGGY, YGGYG, YGYGY, YYGGG
Resumimos.
1. Permutaciones circulares
El número de permutaciones de n elementos en un círculo es
\[(n -1)! \nonumber \]
2. Permutaciones con elementos similares
El número de permutaciones de n elementos tomados n a la vez, con\(r_1\) elementos de un tipo,\(r_2\) elementos de otro tipo, y así sucesivamente, tal que\(\mathrm{n}=\mathrm{r}_{1}+\mathrm{r}_{2}+\ldots+\mathrm{r}_{\mathrm{k}}\) es
\[\frac{n !}{r_{1} ! r_{2} ! \dots r_{k} !} \nonumber \]
Esto también se conoce como particiones ordenadas.


