8.3: Probabilidad usando diagramas de árbol y combinaciones
- Page ID
- 113781
En esta sección, aprenderás a:
- Usar diagramas de árbol de probabilidad para calcular probabilidades
- Usar combinaciones para calcular probabilidades
En esta sección, aplicaremos técnicas de conteo previamente aprendidas en el cálculo de probabilidades, y usaremos diagramas de árbol para ayudarnos a comprender mejor lo que implica.
USAR DIAGRAMAS DE ÁRBOL PARA CALCULAR PROBABILIDADES
Ya usamos diagramas de árbol para enumerar eventos en un espacio de muestra. Los diagramas de árbol pueden ser útiles para organizar la información en problemas de probabilidad; ayudan a proporcionar una estructura para comprender la probabilidad. En esta sección ampliamos nuestro uso previo de diagramas de árbol a situaciones en las que los eventos en el espacio de muestra no son todos igualmente probables.
Asignamos las probabilidades apropiadas a los eventos que se muestran en las ramas del árbol.
Al multiplicar las probabilidades a lo largo de un camino a través del árbol, podemos encontrar probabilidades de eventos “y”, que son intersecciones de eventos.
Comenzamos con un ejemplo.
Supongamos que un frasco contiene 3 canicas rojas y 4 blancas. Si se dibujan dos canicas con reemplazo, ¿cuál es la probabilidad de que ambas canicas sean rojas?
Solución
\(\mathrm{E}\)Sea el evento de que el primer mármol dibujado sea rojo, y que\(\mathrm{F}\) sea el evento de que el segundo mármol dibujado sea rojo.
Tenemos que encontrar\(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\).
Por el comunicado, “se dibujan dos mármoles con reemplazo”, queremos decir que el primer mármol se reemplaza antes de que se dibuje el segundo mármol.
Hay 7 opciones para el primer sorteo. Y dado que el primer mármol se sustituye antes de que se dibuje el segundo, hay, nuevamente, siete opciones para el segundo sorteo. Usando el axioma de multiplicación, concluimos que el espacio muestral\(\mathrm{S}\) consta de 49 pares ordenados. De los 49 pares ordenados, hay pares\(3 \times 3 = 9\) ordenados que muestran rojo en el primer sorteo y, también, rojo en el segundo sorteo. Por lo tanto,
\[P(E \cap F)=\frac{9}{49} \nonumber \]
Obsérvese además que en este caso particular
\[P(E \cap F)=\frac{9}{49}=\frac{3}{7} \cdot \frac{3}{7} \nonumber \]
dándonos el resultado de que en este ejemplo:\(\mathbf{P}(\mathbf{E} \cap \mathbf{F})=\mathbf{P}(\mathbf{E}) \cdot \mathbf{P}(\mathbf{F})\)
Si en Ejemplo\(\PageIndex{1}\), las dos canicas se dibujan sin reemplazo, entonces ¿cuál es la probabilidad de que ambas canicas sean rojas?
Solución
Por el comunicado, “se dibujan dos canicas sin reemplazo”, queremos decir que el primer mármol no se reemplaza antes de que se dibuje el segundo mármol.
Nuevamente, tenemos que encontrar\(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\).
Hay, nuevamente, 7 opciones para el primer sorteo. Y dado que el primer mármol no se sustituye antes de que se dibuje el segundo, sólo hay seis opciones para el segundo sorteo. Usando el axioma de multiplicación, concluimos que el espacio muestral S consiste en 42 pares ordenados. De los 42 pares ordenados, hay pares\(3 \times 2 = 6\) ordenados que muestran rojo en el primer sorteo y rojo en el segundo sorteo. Por lo tanto,
\[P(E \cap F)=\frac{6}{42} \nonumber \]
Tenga en cuenta que podemos desglosar este cálculo como
\[P(E \cap F)=\frac{6}{42}=\frac{3}{7} \cdot \frac{2}{6} \nonumber \].
Aquí 3/7 representa\(\mathrm{P}(\mathrm{E})\), y 2/6 representa la probabilidad de dibujar un rojo en el segundo empate, dado que el primer empate resultó en un rojo.
Escribimos este último como\(\mathrm{P}\) (rojo en el segundo | rojo en el primero) o\(\mathrm{P}(\mathrm{F} | \mathrm{E})\). El “|” representa la palabra “dado” o “si”. Esto lleva al resultado de que:
\[\mathbf{P}(\mathbf{E} \cap \mathbf{F})=\mathbf{P}(\mathbf{E}) \cdot \mathbf{P}(\mathbf{F} | \mathbf{E}) \nonumber \]
El es un resultado importante, denominado Regla de Multiplicación, que volverá a aparecer en secciones posteriores.
Ahora demostramos los resultados anteriores con un diagrama de árbol.
Supongamos que un frasco contiene 3 canicas rojas y 4 blancas. Si se dibujan dos canicas sin reemplazo, encuentre las siguientes probabilidades usando un diagrama de árbol.
- La probabilidad de que ambas canicas sean rojas.
- La probabilidad de que el primer mármol sea rojo y el segundo blanco.
- La probabilidad de que una canica sea roja y la otra blanca.
Solución
\(\mathrm{R}\)Sea el evento de que el mármol dibujado sea rojo, y que W sea el evento de que el mármol dibujado sea blanco.
Dibujamos el siguiente diagrama de árbol.
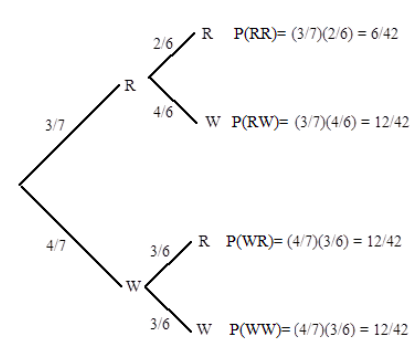
- La probabilidad de que ambas canicas sean rojas es\(\mathrm{P}(\mathrm{RR})=6/42\)
- La probabilidad de que el primer mármol sea rojo y el segundo sea blanco es\(\mathrm{P}(\mathrm{RW})=12/42\)
- Por la probabilidad de que una canica sea roja y la otra sea blanca, observamos que esto puede satisfacerse si la primera es roja y la segunda es blanca, o si la primera es blanca y la segunda es roja. El “o” nos dice que usaremos la Regla de Adición de la Sección 7.2.
Además, los eventos\(\mathrm{RW}\) y\(\mathrm{WR}\) son eventos mutuamente excluyentes, por lo que utilizamos la forma de la Regla de Adición que se aplica a eventos mutuamente excluyentes.
Por lo tanto
\(\mathrm{P}\)(un mármol es rojo y el otro es blanco)
\ [\ begin {array} {l}
=\ mathrm {P} (\ mathrm {RW}\ texto {o}\ mathrm {WR})\\
=\ mathrm {P} (\ mathrm {RW}) +\ mathrm {P} (\ mathrm {WR})\\
=12/42+12/42=24/42
\ end {array}\ nonumber\]
USAR COMBINACIONES PARA ENCONTRAR PROBABILIDADES
Aunque los diagramas de árboles nos dan una mejor visión de un problema, no son prácticos para problemas donde se eligen más de dos o tres cosas. En tales casos, utilizamos el concepto de combinaciones que aprendimos en el último capítulo. Este método es el más adecuado para problemas donde el orden en el que se eligen los objetos no es importante, y los objetos se eligen sin reemplazo.
Supongamos que un frasco contiene 3 canicas rojas, 2 blancas y 3 azules. Si se dibujan tres canicas sin reemplazo, encuentre las siguientes probabilidades.
- \(\mathrm{P}\)(Dos rojos y uno blanco)
- \(\mathrm{P}\)(Uno de cada color)
- \(\mathrm{P}\)(Ninguno azul)
- \(\mathrm{P}\)(Al menos un azul)
Solución
Supongamos que las canicas están etiquetadas como\(R_1,R_2,R_3,W_1,W_2,B_1,B_2,B_3\).
a.\(\mathrm{P}\) (Dos rojos y uno blanco)
Ya que estamos eligiendo 3 canicas de un total de 8, hay 8\(\mathrm{C}\) 3 = 56 combinaciones posibles. De estas 56 combinaciones, hay\(3 \mathrm{C} 2 \times 2 \mathrm{C}1=6\) combinaciones que constan de 2 rojas y una blanca. Por lo tanto,
\[P(\text { Two red and one white })=\frac{3 \mathrm{C} 2 \times 2 \mathrm{C} 1}{8 \mathrm{C} 3}=\frac{6}{56} \nonumber. \nonumber \]
b.\(\mathrm{P}\) (Uno de cada color)
Nuevamente, hay 8\(\mathrm{C}\) 3 = 56 combinaciones posibles. De estas 56 combinaciones, hay\(3 \mathrm{Cl} \times 2 \mathrm{Cl} \times 3 \mathrm{Cl}=18\) combinaciones que consisten en una roja, una blanca y una azul. Por lo tanto,
\[P(\text { One of each color })=\frac{3 \mathrm{C} 1 \times 2 \mathrm{C} 1 \times 3 \mathrm{C} 1}{8 \mathrm{C} 3}=\frac{18}{56} \nonumber \]
c.\(\mathrm{P}\) (Ninguno azul)
Hay 5 canicas no azules, por lo tanto
\[\mathrm{P}(\text { None blue })=\frac{5 \mathrm{C} 3}{8 \mathrm{C} 3}=\frac{10}{56}=\frac{5}{28} \nonumber \]
d.\(\mathrm{P}\) (Al menos un azul)
Por “al menos un mármol azul”, nos referimos a lo siguiente: un mármol azul y dos canicas no azules, O dos canicas azules y una mármol no azul, O las tres canicas azules. Entonces tenemos que encontrar la suma de las probabilidades de los tres casos.
\[\mathrm{P}(\mathrm{At} \text { least one blue })=\mathrm{P}(1 \text { blue, } 2 \text { non-blue) }+\mathrm{P}(2 \text { blue, l non-blue) }+\mathrm{P}(3\text { blue) } \nonumber \]
\[P( \text { At least one blue })=\frac{3 \mathrm{C} 1 \times 5 \mathrm{C} 2}{8 \mathrm{C} 3}+\frac{3 \mathrm{C} 2 \times 5 \mathrm{C} 1}{8 \mathrm{C} 3}+\frac{3 \mathrm{C} 3}{8 \mathrm{C} 3} \nonumber \]
\[ P(\text { At least one blue })=30 / 56+15 / 56+1 / 56=46 / 56=23 / 28 \nonumber \]
Como alternativa, podemos aprovechar el hecho de que\(\mathrm{P}(\mathrm{E}) = 1 - \mathrm{P}(\mathrm{E}^c)\). Si el evento\(\mathrm{E}\) = Al menos un azul, entonces\(E^c\) = Ninguno azul.
Pero de la parte c de este ejemplo, tenemos\((\mathrm{E}^c) = 5/28\), así\(\mathrm{P}(\mathrm{E}) = 1 - 5/28 = 23/28\).
Se extraen cinco cartas de una baraja. Encuentra la probabilidad de obtener dos pares, es decir, dos cartas de un valor, dos de otro valor y otra carta.
Solución
Primero hagamos un problema más fácil: la probabilidad de obtener un par de reyes y reinas.
Como hay cuatro reyes, y cuatro reinas en la baraja, la probabilidad de obtener dos reyes, dos reinas y otra carta es
\[\mathrm{P}(\mathrm{A} \text { pair of kings and queens })=\frac{4 \mathrm{C} 2 \times 4 \mathrm{C} 2 \times 44 \mathrm{C}1}{52 \mathrm{C} 5} \nonumber \]
Para encontrar la probabilidad de obtener dos pares, hay que considerar todos los pares posibles.
Dado que hay en total 13 valores, es decir, ases, deuces, y así sucesivamente, hay 13\(\mathrm{C}\) 2 combinaciones diferentes de pares.
\[P(\text { Two pairs })=13 \mathrm{C} 2 \cdot \frac{4 \mathrm{C} 2 \times 4 \mathrm{C} 2 \times 44 \mathrm{C}1}{52 \mathrm{C} 5}=.04754 \nonumber \]
Una tienda de celulares recibe un envío de 15 celulares que contiene 8 iPhones y 7 teléfonos Android. Supongamos que se seleccionan al azar 6 celulares de este envío. Encuentra la probabilidad de que un conjunto seleccionado al azar de 6 celulares consista en 2 iPhones y 4 teléfonos Android.
Solución
Hay 8\(\mathrm{C}\) 2 formas de seleccionar 2 de los 8 iPhones.
y 7\(\mathrm{C}\) 4 formas de seleccionar 4 de los 7 teléfonos Android
Pero en conjunto hay 15\(\mathrm{C}\) 6 formas de seleccionar 6 de cada 15 celulares.
Por lo tanto tenemos
\[P(2 \text { iPhones and } 4 \text { Android phones })=\frac{8 \mathrm{C} 2 \times 7 \mathrm{C} 4}{15 \mathrm{C} 6}=\frac{(28)(35)}{5005}=\frac{980}{5005}=0.1958 \nonumber \]
Una tarde, una tienda de bagels aún tiene 53 bagels restantes: 20 bagels simples, 15 de semillas de amapola y 18 bagels de semillas de sésamo. Supongamos que el dueño de la tienda empaqueta una bolsa de 9 bagels para llevar a casa para el desayuno de mañana, y selecciona los bagels al azar. Encuentra la probabilidad de que la bolsa contenga 4 semillas simples, 3 semillas de amapola y 2 semillas de sésamo.
Solución
Hay 20\(\mathrm{C}\) 4 formas de seleccionar 4 de los 20 bagels lisos,
y 15\(\mathrm{C}\) 3 formas de seleccionar 3 de los 15 bagels de semillas de amapola,
y 18\(\mathrm{C}\) 2 formas de seleccionar 2 de los 18 bagels de semillas de sésamo.
Pero en conjunto hay 53\(\mathrm{C}\) 9 formas de seleccionar 9 de los 53 bagels.
\ begin {array} {l}
\ mathrm {P}\ text {(4 simples, 3 semillas de amapola y 2 semillas de sésamo)} &=\ frac {20\ mathrm {C} 4\ times 15\ mathrm {C} 3\ times 18\ mathrm {C} 2} {53\ mathrm {C} 9}\\
&=\ frac {(4845) (455) (153)} {4431613550}\\
&=0.761
\ end {array}
Terminamos la sección resolviendo un famoso problema llamado el Problema del Cumpleaños.
Si hay 25 personas en una habitación, ¿cuál es la probabilidad de que al menos dos personas tengan el mismo cumpleaños?
Solución
Que el\(\mathrm{E}\) evento represente que al menos dos personas tengan el mismo cumpleaños.
Primero encontramos la probabilidad de que no dos personas tengan el mismo cumpleaños.
Analizamos de la siguiente manera.
Supongamos que hay 365 días para cada año. Según el axioma de multiplicación, hay 365 25 cumpleaños posibles para 25 personas. Por lo tanto, el espacio muestral cuenta con 365 25 elementos. Nos interesa la probabilidad de que no haya dos personas que cumplan el mismo cumpleaños. Hay 365 opciones posibles para la primera persona y como la segunda persona debe tener un cumpleaños diferente, hay 364 opciones para la segunda, 363 para la tercera, y así sucesivamente. Por lo tanto,
\[\mathrm{P}(\mathrm{No} \text { two have the same birthday })=\frac{365 \cdot 364 \cdot 363 \cdots 341}{365^{25}}=\frac{365 \mathrm{P} 25}{365^{25}} \nonumber \]
Ya que\(\mathrm{P}\) (al menos dos personas tienen el mismo cumpleaños) = 1 -\(\mathrm{P}\) (No hay dos que tengan el mismo cumpleaños),
\[\mathrm{P} \text { at least two people have the same birthday ) }=1-\frac{365 \mathrm{P} 25}{365^{25}}=.5687\ \nonumber \]


