9.2: Fórmula de Bayes
- Page ID
- 113871
En esta sección, aprenderás a:
- Encuentra probabilidades usando la fórmula de Bayes
- Utilice un árbol de probabilidad para encontrar y representar los valores necesarios al usar la fórmula de Bayes.
En esta sección, desarrollaremos y utilizaremos la Fórmula de Bayes para resolver un importante tipo de problema de probabilidad. La fórmula de Bayes es un método para calcular la probabilidad condicional\(P(F | E)\) a partir de\(P(E | F)\). Las ideas aquí involucradas no son nuevas, y la mayoría de estos problemas se pueden resolver usando un diagrama de árbol. Sin embargo, la fórmula de Bayes sí nos proporciona una herramienta con la que podemos resolver estos problemas sin un diagrama de árbol.
Comenzamos con un ejemplo.
Supongamos que le dan dos frascos. El Jar I contiene una canica negra y 4 canicas blancas, y la Jarra II contiene 4 canicas negras y 6 blancas. Si se selecciona un frasco al azar y se elige una canica,
- ¿Cuál es la probabilidad de que el mármol elegido sea un mármol negro?
- Si el mármol elegido es negro, ¿cuál es la probabilidad de que provenga de Jar I?
- Si el mármol elegido es negro, ¿cuál es la probabilidad de que provenga del Jar II?
Solución
\(J I\)Sea el evento que se elija a Jar I,\(J II\) sea el evento que se elija a Jar II,\(B\) sea el evento que se elija un mármol negro y\(W\) el evento que se elija un mármol blanco.
Ilustramos usando un diagrama de árbol.
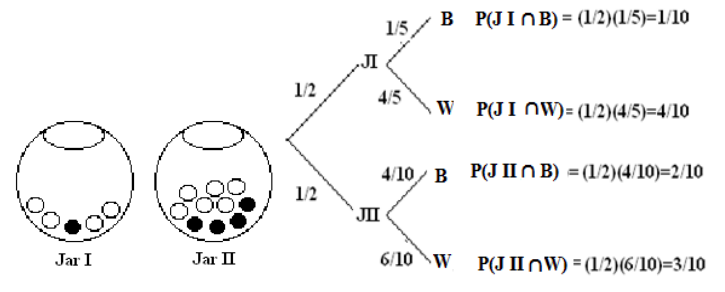
- La probabilidad de que se elija un mármol negro es\(P(B)\) = 1/10 + 2/10 = 3/10.
- Para encontrar\(P(J I | B)\), usamos la definición de probabilidad condicional, y obtenemos\[P(J I | B)=\frac{P(J I \cap B)}{P(B)}=\frac{1 / 10}{3 / 10}=\frac{1}{3} \nonumber \]
- Del mismo modo,\(\mathrm{P}(\mathrm{J} \mathrm{II} | \mathrm{B})=\frac{\mathrm{P}(\mathrm{J} \mathrm{II} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}=\frac{2 / 10}{3 / 10}=\frac{2}{3}\)
En las partes b y c, el lector debe señalar que el denominador es la suma de todas las probabilidades de todas las ramas del árbol que producen un mármol negro, mientras que el numerador es la rama que está asociada con el frasco particular en cuestión.
Pronto descubriremos que esta es una declaración de la fórmula de Bayes.
Primero visualicemos el problema.
Se nos da un espacio de muestra\(\mathrm{S}\) y dos eventos mutuamente excluyentes\(J I\) y\(J II\). Es decir, los dos eventos,\(J I\) y\(J II\), dividir el espacio muestral en dos partes de tal manera que\(\mathrm{JI} \cup \mathrm{JII}=\mathrm{S}\). Además, se nos da un evento\(B\) que tiene elementos en ambos\(J I\) y\(J II\), como se muestra en el diagrama de Venn a continuación.
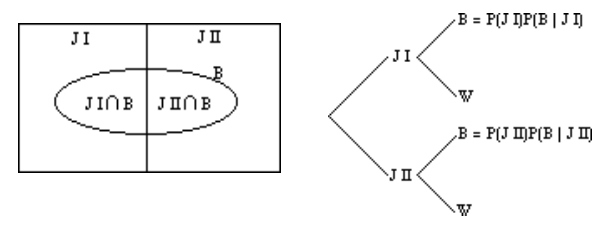
Del diagrama de Venn, podemos ver que\(\mathrm{B}=(\mathrm{B} \cap \mathrm{J} \mathrm{I}) \cup(\mathrm{B} \cap \mathrm{J} \mathrm{II})\) Por lo tanto:
\[ P(B)=P(B \cap J I)+P(B \cap J I I) \label{I} \]
Pero la regla del producto en el capítulo 7 nos da
\[ P(B \cap J I)=P(J I) \cdot P(B | J I) \quad \text { and } \quad P(B \cap J I I)=P(J I I) \cdot P(B | J I I) \nonumber \]
Sustituyendo en\ ref {I}, obtenemos
\[P(B)=P(J I) \cdot P(B | J I)+P(J I I) \cdot P(B | J I I) \nonumber \]
La fórmula de probabilidad condicional nos da
\[P(J I | B)=\frac{P(J I \cap B)}{P(B)} \nonumber \]
Por lo tanto,\(P(J I | B)=\frac{P(J I) \cdot P(B | J I)}{P(B)}\)
o
\[P(J I | B)=\frac{P(J I) \cdot P(B | J I)}{P(J I) \cdot P(B | J I)+P(J I I) \cdot P(B | J I I)} \nonumber \]
El último enunciado es la fórmula de Bayes para el caso en el que el espacio muestral se divide en dos particiones.
A continuación se presenta la generalización de la fórmula de Bayes para n particiones.
Dejar\(\mathrm{S}\) ser un espacio de muestra que se divide en\(n\) particiones\(A_1\),\(A_2\),,.. \(A_n\). Si\(E\) hay algún evento en\(\mathrm{S}\), entonces
\[\mathbf{P}\left(\mathbf{A}_{\mathbf{i}} | \mathbf{E}\right)=\frac{\mathbf{P}\left(\mathbf{A}_{\mathbf{i}}\right) \mathbf{P}\left(\mathbf{E} | \mathbf{A}_{\mathbf{i}}\right)}{\mathbf{P}\left(\mathbf{A}_{\mathbf{1}}\right) \mathbf{P}\left(\mathbf{E} | \mathbf{A}_{\mathbf{1}}\right)+\mathbf{P}\left(\mathbf{A}_{2}\right) \mathbf{P}\left(\mathbf{E} | \mathbf{A}_{2}\right)+\cdots+\mathbf{P}\left(\mathbf{A}_{\mathbf{n}}\right) \mathbf{P}\left(\mathbf{E} | \mathbf{A}_{\mathbf{n}}\right)} \nonumber \]
Comenzamos con el siguiente ejemplo.
Una tienda departamental compra 50% de sus electrodomésticos al Fabricante A, 30% al Fabricante B y 20% al Fabricante C. Se estima que 6% de los electrodomésticos del Fabricante A, 5% de los electrodomésticos del Fabricante B y 4% de los electrodomésticos del Fabricante C necesitan reparación antes de que expire la garantía. Se elige un aparato al azar. Si el aparato elegido necesitaba reparación antes de que expirara la garantía, ¿cuál es la probabilidad de que el electrodoméstico haya sido fabricado por el Fabricante A? Fabricante B? Fabricante C?
Solución
Que A, B y C sean los eventos en los que el aparato sea fabricado por el Fabricante A, el Fabricante B y el Fabricante C, respectivamente. Además, supongamos que el evento R denota que el aparato necesita reparación antes de que expire la garantía.
Necesitamos encontrar P (A | R), P (B | R) y P (C | R).
Haremos este problema tanto usando un diagrama de árbol como usando la fórmula de Bayes.
Dibujamos un diagrama de árbol.
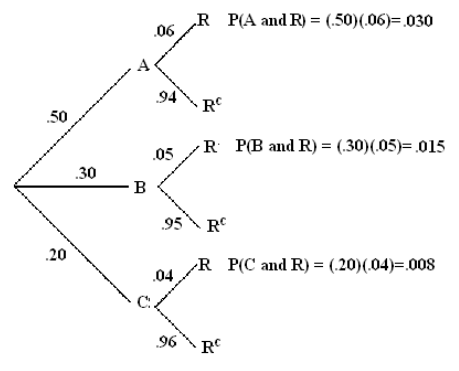
La probabilidad P (A | R), por ejemplo, es una fracción cuyo denominador es la suma de todas las probabilidades de todas las ramas del árbol que dan como resultado un aparato que necesita reparación antes de que expire la garantía, y el numerador es la rama que está asociada al Fabricante A. P (B | R) y P (C | R) se encuentran en de la misma manera.
\ [\ begin {array} {l}
P (A | R) =\ frac {.030} {(.030) + (.015) + (.008)} =\ frac {.030} {.053} =.566\
P (B | R) =\ frac {.015} {.053} =.283\ text {y} P (C | R) =\ frac {.008} {.053} =.151
\ end {array}\ nonumber\]
Alternativamente, usando la fórmula de Bayes,
\ begin {alineado}
\ mathrm {P} (\ mathrm {A} |\ mathrm {R}) &=\ frac {\ mathrm {P} (\ mathrm {A})\ mathrm {P} (\ mathrm {R} |\ mathrm {A})} {\ mathrm {P} (\ mathrm {A})\ mathrm {P} (\ mathrm {R} |\ mathrm {A}) +\ mathrm {P} (\ mathrm {B})\ mathrm {P} (\ mathrm {R} |\ mathrm {B}) +\ mathrm {P} (\ mathrm {C})\ mathrm {P} (\ mathrm {R} |\ mathrm {C} )}\\
&=\ frac {.030} {(.030) + (.015) + (.008)} =\ frac {.030} {.053} =.566
\ end {alineado}
P (B | R) y P (C | R) se pueden determinar de la misma manera.
Hay cinco tiendas departamentales Jacy's en San José. La distribución del número de empleados por género se da en la siguiente tabla.
| Número de tienda | Número de empleados | Porcentaje de mujeres empleadas |
| 1 | 300 | .40 |
| 2 | 150 | .65 |
| 3 | 200 | .60 |
| 4 | 250 | .50 |
| 5 | 100 | .70 |
| Total = 1000 |
Si un empleado elegido al azar es una mujer, ¿cuál es la probabilidad de que el empleado trabaje en la tienda III?
Solución
Let\(k\) = 1, 2,.., 5 sea el evento que el empleado trabajó en tienda\(k\), y W sea el evento de que el empleado sea una mujer. Dado que hay un total de 1000 empleados en las cinco tiendas,
\[P(1)=.30 \quad P(2)=.15 \quad P(3)=.20 \quad P(4)=.25 \quad P(5)=.10 \nonumber \]
Usando la fórmula de Bayes,
\ [\ begin {array} {l}
\ mathrm {P} (3 |\ mathrm {W}) &=\ frac {\ mathrm {P} (3)\ mathrm {P} (\ mathrm {W} | 3)} {\ mathrm {P} (1)\ mathrm {P} (\ mathrm {P} (\ mathrm {W} | 1) +\ mathrm {P} (2)\ mathrm {P} (\ mathrm {W} | 2) +\ mathrm {P} (3)\ mathrm {P} (\ mathrm {W} | 3) +\ mathrm {P} (4)\ mathrm {P} (\ mathrm {W} | 4) +\ mathrm {P} (5)\ mathrm {P} (\ mathrm {W} | 5)}\\
&=\ frac {(.20) (.60)} {(.30) (.40) + (.15) (.65) + (.20) (.60) + (.25) (.50) + (.10) (.70)}\\
&=.2254
\ end {array}\ nonumber\]


