11.1: Juegos estrictamente determinados

Última actualización
Guardar como PDF

Page ID: 113757

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En este capítulo, estudiaremos los juegos que involucran sólo a dos jugadores. En estos juegos, dado que una victoria para una persona es una pérdida para la otra, nos referimos a ellos como juegos de suma cero de dos personas. Aunque los juegos que estudiaremos aquí son bastante simples, nos proporcionarán una comprensión de cómo funcionan los juegos y cómo se aplican en situaciones prácticas. Comenzamos con un ejemplo.

Ejemplo$\PageIndex{1}$

Robert y Carol deciden jugar un juego usando un centavo y un cuarto. Cada uno elige una de las dos monedas, la pone en la mano y cierra el puño. A una señal dada, simultáneamente abren los puños. Si la suma de las monedas es inferior a 35 centavos, Robert obtiene ambas monedas, de lo contrario, Carol obtiene ambas monedas. Escribe la matriz para el juego, determina las estrategias óptimas para cada jugador y encuentra la rentabilidad esperada para Robert.

Solución

Supongamos que Robert es el jugador de fila, es decir, juega las filas, y Carol es una jugadora de columna. Si Robert muestra una moneda de diez centavos y Carol muestra una moneda de diez centavos, la suma será inferior a treinta y cinco centavos y Robert ganará diez centavos. Pero, si Robert muestra un centavo y Carol muestra un cuarto, la suma no será inferior a treinta y cinco centavos y Carol ganará diez centavos o Robert perderá diez centavos. La siguiente matriz representa los cuatro casos y sus correspondientes pagaciones para Robert. Recuerda que un valor negativo es una pérdida para Robert y una victoria para Carol.

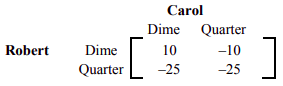
$Ejemplo11.1.1.png$

La mejor estrategia para Robert es mostrar siempre un centavo porque de esta manera lo peor que puede hacer es perder diez centavos. Y, la mejor estrategia para Carol es mostrar siempre un cuarto porque así lo peor que puede hacer es perder diez centavos. Si tanto Robert como Carol juegan sus estrategias óptimas, Robert perderá diez centavos cada vez. Por lo tanto, el valor del juego es negativo diez centavos.

En el ejemplo anterior, dado que solo hay una estrategia óptima fija para cada jugador, independientemente de la estrategia de su oponente, decimos que el juego posee una estrategia pura y está estrictamente determinado.

A continuación, formulamos un método para encontrar la estrategia óptima para cada jugador y el valor del juego. El método implica considerar el peor escenario para cada jugador.

Para considerar la peor situación, el jugador de fila considera el valor mínimo en cada fila, y el jugador de columna considera el valor máximo en cada columna. Tenga en cuenta que el valor máximo realmente representa un valor mínimo para el jugador de columna porque la matriz del juego representa los pyoffs para el jugador de fila. Enumeramos el método a continuación.

Encontrar la estrategia óptima y el valor para los juegos estrictamente determinados

Poner un asterisco (*) junto a la entrada mínima en cada fila.
Ponga una caja alrededor de la entrada máxima en cada columna.
La entrada que tiene tanto un asterisco como una caja representa el valor del juego y se llama punto de silla de montar.
La fila que está asociada con el punto de sillín representa la mejor estrategia para el jugador de fila, y la columna que está asociada con el punto de silla representa la mejor estrategia para el jugador de columna.
Una matriz de juego puede tener más de un punto de sillín, pero todos los puntos de sillín tienen el mismo valor.
Si no existe un punto de silla de montar, el juego no está estrictamente determinado. Los juegos no estrictamente determinados son el tema de la siguiente sección.

Ejemplo$\PageIndex{2}$

Encuentra los puntos de sillín y las estrategias óptimas para el siguiente juego.

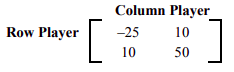
$Ejemplo11.1.1A.png$

Solución

Encontramos el punto de sillín colocando un asterisco junto a la entrada mínima en cada fila, y poniendo una caja alrededor de la entrada máxima en cada columna como se muestra a continuación.

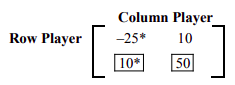
$Ejemplo11.1.1b.png$

Dado que la segunda fila, primera entrada de columna, que pasa a ser 10, tiene tanto un asterisco como una caja, es un punto de silla de montar. Esto implica que el valor del juego es 10, y la estrategia óptima para el jugador de fila es jugar siempre la fila 2, y la estrategia óptima para el jugador de columna es jugar siempre la columna 1. Si ambos jugadores juegan sus estrategias óptimas, el jugador de fila ganará 10 unidades cada vez.

La estrategia del jugador de fila se escribe como\ (\ left [\ begin {array} {ll}
0 & 1
\ end {array}\ right]\) indicando que jugará la fila 1 con una probabilidad de 0 y la fila 2 con una probabilidad de 1.

De igual manera la estrategia del jugador de columna se escribe como\ (\ left [\ begin {array} {l}
1\
\
0\ end {array}\ right]\) implicando que jugará la columna 1 con una probabilidad de 1, y la columna 2 con una probabilidad de 0.

Ejemplo\(\PageIndex{1}\)

Encontrar la estrategia óptima y el valor para los juegos estrictamente determinados

Ejemplo\(\PageIndex{2}\)