4.1: Sumando números impares

¿Alguna vez has trabajado a través de una prueba, entendido y confirmado cada paso, pero todavía no creyó el teorema? Te das cuenta de que el teorema es cierto, pero no por qué es cierto.

Para ver el mismo contraste en un ejemplo familiar, imagínese aprender que su hijo tiene fiebre y escuchar la temperatura en grados Fahrenheit o Celsius, lo que sea menos familiar. En mi experiencia diaria, las temperaturas son mayormente en Fahrenheit. Cuando oigo hablar de una temperatura de\(40^{◦}C\), por lo tanto, reacciono en dos etapas:

1. Convierto\(40^{◦}C\) a Fahrenheit:\(40 \times 1.8 + 32 = 104.\)
2. Yo reacciono: “Guau,\(104^{◦}F\). ¡Eso es peligroso! ¡Llévente a un médico!”

La temperatura Celsius, aunque simbólicamente equivalente a la temperatura Fahrenheit, no provoca ninguna reacción. Mi sentido de peligro se activa solo después de que la conversión de temperatura conecta la temperatura a mi experiencia.

Una descripción simbólica, ya sea una prueba o una temperatura desconocida, es poco convincente en comparación con un argumento que habla de nuestro sistema perceptivo. La razón radica en cómo nuestros cerebros adquirieron la capacidad de razonamiento simbólico. (Ver Cerebros evolutivos [2] para una historia académica ilustrada del cerebro.) El razonamiento simbólico y secuencial requiere lenguaje, que ha evolucionado solo por\(10^{5}\) año. Aunque\(10^{5}\) yr abarca muchas vidas humanas, es un parpadeo evolutivo. En particular, es corto en comparación con el lapso de tiempo durante el cual nuestro hardware perceptual ha evolucionado: Durante varios cientos de millones de años, los organismos han refinado sus capacidades para escuchar, oler, saborear, tocar y ver.

La evolución ha trabajado 1000 veces más en nuestras habilidades perceptuales que en nuestras habilidades de razonamiento simbólico. Comparado con nuestro hardware perceptual, nuestro hardware simbólico y secuencial es un recién llegado poco desarrollado. No es sorprendente que nuestras habilidades perceptuales superen con creces nuestras habilidades simbólicas. Incluso una actividad simbólica aparentemente de alto nivel como jugar al ajedrez de gran maestro utiliza principalmente hardware perceptual [16]. Ver una idea nos transmite una profundidad de comprensión que una descripción simbólica de la misma no puede igualar fácilmente.

Múltiples problemas

Problema 4.1 Computadoras versus personas

En tareas como expandirse\((x + 2y)^{50}\), las computadoras son mucho más rápidas que las personas. En tareas como reconocer rostros u olores, incluso los niños pequeños son mucho más rápidos que las computadoras actuales. ¿Cómo explicas estos contrastes?

Problema 4.2 Evidencia lingüística de la importancia de la percepción

En tu (s) idioma (s) favorito (s), piensa en los muchos sinónimos sensoriales para estar de pie (por ejemplo, agarrar).

Sumando números impares

Para ilustrar el valor de las imágenes, encontremos la suma de los primeros números\(n\) impares (también el tema del Problema 2.25):

\[S_{n} = \underbrace{1 + 3 + 5 + ... + (2n - 1).}_{n \text{terms}} \label{4.1} \]

Casos fáciles como\(n\) = 1, 2, o 3 llevan a la conjetura de que\(S_{n} = n^{2}\). Pero, ¿cómo se puede probar la conjetura? El método simbólico estándar es la prueba por inducción:

1. Verifica que\(S_{n}\) =\(n^{2}\) para el caso base\(n = 1\). En ese caso,\(S_{1}\) es 1, como es\(n_{2}\), por lo que se verifica el caso base.

2. Hacer la hipótesis de inducción: Supongamos que\(S_{m}\) =\(m^{2}\) para m menor o igual a un valor máximo n. Para esta prueba, es suficiente la siguiente hipótesis de inducción más débil:

\[\sum_{1}^{n} (2k - 1) = n^{2} \label{4.2} \]

En otras palabras, asumimos el teorema sólo en el caso de que\(m = n\).

3. Realizar el paso de inducción: Utilizar la hipótesis de inducción para mostrar que\(S_{n+1}\) = (n + 1)\(^{2}\). La suma\(S_{n+1}\) se divide en dos partes:

\[S_{n+1}=\sum_{1}^{n+1}(2 k-1)=(2 n+1)+\sum_{1}^{n}(2 k-1)\label{4.3} \]

Gracias a la hipótesis de inducción, la suma de la derecha es\(n^{2}\). Así

\[S_{n+1} = (2n + 1) + n^{2}, \label{4.4} \]

que es\((n + 1)^{2}\); y se prueba el teorema.

Si bien estos pasos prueban el teorema, por qué la suma\(S_{n}\) termina como\(n^{2}\) todavía se siente esquiva.

Esa falta de comprensión del tipo de perspicacia gestáltica descrita por Wertheimer [48] requiere una prueba pictórica. Comience dibujando cada número impar como una pieza de rompecabezas en forma de L:

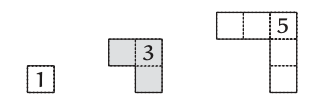\[\label{4.5} \]

Pregunta

¿Cómo encajan estas piezas?

Luego computa\(S_{n}\) juntando las piezas del rompecabezas de la siguiente manera:

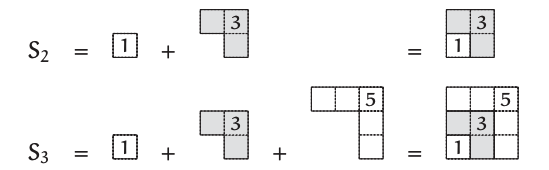\[label{4.6} \nonumber \]

Cada número impar sucesivo cada pieza extiende el cuadrado por 1 unidad en altura y ancho, por lo que los\(n\) términos construyen un\(n \times n\) cuadrado. [¿O es un\((n − 1) \times (n − 1)\) cuadrado?] Por lo tanto, su suma es\(n^{2}\). Después de agarrar esta prueba pictórica, no se puede olvidar por qué la suma de los primeros n números impares produce\(n^{2}\).

Múltiples problemas

Problema 4.3 Números triangulares

Dibuja un cuadro o imágenes para mostrar eso

\[1 + 2 + 3 + ··· + n + ··· + 3 + 2 + 1 = n^{2}. \label{4.7} \]

Entonces demuéstralo

\[1 + 2 + 3 + ··· + n = \frac{n(n+1)}{2}.\label{4.8} \]

Problema 4.4 Tres dimensiones

Dibuja una imagen para mostrar que

\[\sum_{0}^{n} (3k^{2} + 3k + 1) = (n + 1)^{3}. \label{4.9} \]

Dar explicaciones pictóricas para el 1 en el summand\(3k^{2} + 3k + 1\); para el 3 y el\(k^{2}\) in\(3k^{2}\); y para el 3 y el k en 3k.