4.2: Medias aritméticas y geométricas
- Page ID
- 112479
La siguiente prueba pictórica comienza con dos números no negativos por ejemplo, 3 y 4 y compara los dos promedios siguientes:
\[\text{ arithmetic mean } ≡ \frac{3 + 4}{2} = 3/5; \label{4.10} \]
\[\text{ geometric mean } ≡ \sqrt{3 \times 4} ≈ 3.464. \label{4.11} \]
Prueba otro par de números por ejemplo, 1 y 2. La media aritmética es 1.5; la media geométrica es\(\sqrt{2} ≈ 1.414\). Para ambos pares, la media geométrica es menor que la media aritmética. Este patrón es general; es la famosa desigualdad aritmética-media-geométrica (AM—GM) [18]:
\ [\ begin {alineado}
&\ underbrackets {\ frac {a+b} {2}} _ {\ text {AM}}\ geqslant\ underbrackets {\ sqrt {a b}} _ {\ text {GM}}\\
&\ text {desigualdad requiere eso} a, b\ geqslant 0.
\ end {alineado}\ etiqueta {4.12}\]
Pruebe la desigualdad AM—GM usando diversos ejemplos numéricos. ¿Qué notas cuando a y b están cerca el uno del otro? ¿Se puede formalizar el patrón? (Ver también Problema 4.16.)
Prueba simbólica
La desigualdad AM—GM tiene una prueba pictórica y simbólica. La prueba simbólica comienza con\((a−b)^{2}\) una elección sorprendente porque la desigualdad contiene\(a + b\) más que\(a − b\). La segunda opción impar es formar\((a − b)^{2}\). Es no negativo, entonces\(a^{2} − 2ab + b^{2} \geqslant 0\). Ahora mágicamente deciden sumar\(4ab\) a ambos lados. El resultado es
\[\underbrace{a^{2} + 2ab + b^{2}}_{(a + b)^{2}} \geqslant 4ab \label{4.13} \]
El lado izquierdo es\((a + b)^{2}\), así\(a + b \geqslant 2 \sqrt{ab}\) y
\[\frac{a + b}{2} \geqslant \sqrt{ab}\label{4.14} \]
Aunque cada paso es sencillo, toda la cadena parece mágica y deja el por qué misterioso. Si el álgebra hubiera terminado con\((a + b)/4 \geqslant ab\), no se vería obviamente mal. En contraste, una prueba convincente nos dejaría sintiendo que la desigualdad no puede dejar de ser cierta.
Prueba pictórica
Esta satisfacción es proporcionada por una prueba pictórica.
¿Qué es pictórica, o geométrica, de la media geométrica?
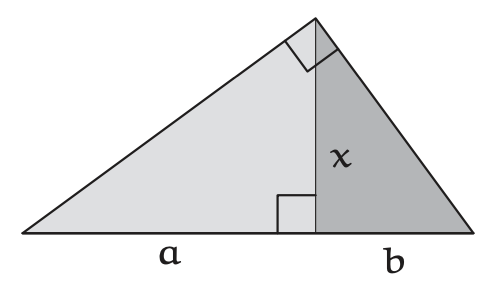
Una imagen geométrica para la media geométrica comienza con un triángulo rectángulo. Colócala con su hipotenusa horizontal; luego córtala con la altitud\(x\) en los subtriángulos claros y oscuros. La hipotenusa se divide en dos longitudes\(a\) y\(b\), y la altitud\(x\) es su media geométrica\(\sqrt{ab}\).
¿Por qué la altitud es\(x\) igual a\(\sqrt{ab}\)?
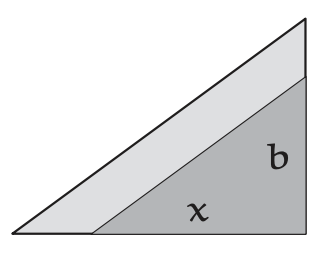
Para demostrarlo\(x = \sqrt{ab}\), compare el pequeño triángulo oscuro con el triángulo grande y ligero girando el triángulo pequeño y colocándolo sobre el triángulo grande. ¡Los dos triángulos son similares! Por lo tanto, sus relaciones de aspecto (la relación del lado corto al lado largo) son idénticas. En símbolos,\(x/a = b/x\): La altitud x es, por tanto, la media geométrica\(\sqrt{ab}\). El triángulo recto sin cortar representa la porción geométrica-media de la desigualdad AM—GM. La media aritmética\((a + b)/2\) también tiene una imagen, como la mitad de la hipotenusa. Así, la desigualdad afirma que
\[\frac{\text{ hypotenuse } }{2} \geqslant \text{ altitude } \label{4.15} \]
Por ay, esta afirmación no es pictóricamente obvia.
¿Se puede encontrar una interpretación geométrica alternativa de la media aritmética que haga que la desigualdad AM—GM sea pictóricamente obvia?
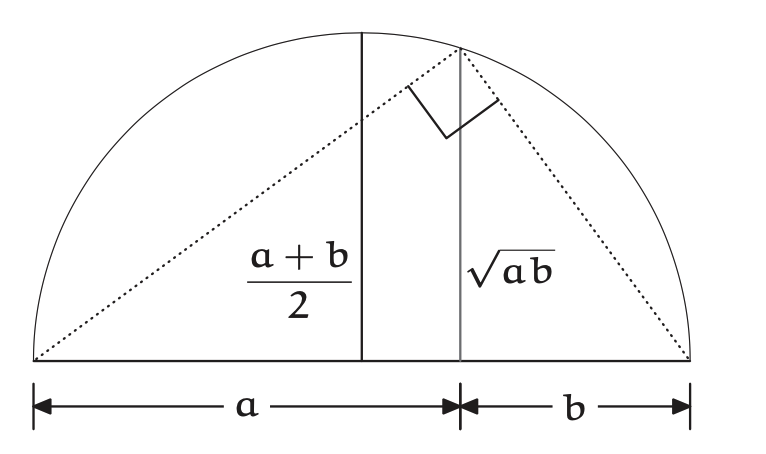
La media aritmética es también el radio de un círculo con diámetro\(a + b\). Por lo tanto, circunscribir un semicírculo alrededor del triángulo, haciendo coincidir el diámetro del círculo con la hipotenusa\(a + b\) (problema 4.7.). La altitud no puede exceder el radio; por lo tanto,
\[\frac{a + b}{2} \geqslant \sqrt{ab} \label{4.16} \]
Además, los dos lados son iguales solo cuando la altitud del triángulo es también un radio del semicírculo, es decir, cuándo\(a = b\). Por lo tanto, la imagen contiene la desigualdad y su condición de igualdad en un objeto fácil de captar. (Una prueba pictórica alternativa de la desigualdad AM—GM se desarrolla en Problema 4.33.)
Problema 4.6 Circunscribir un círculo alrededor de un triángulo
Aquí hay algunos ejemplos que muestran un círculo circunscrito alrededor de un triángulo.
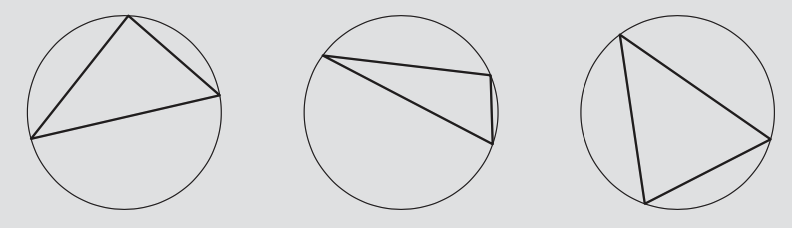
Dibuja una imagen para mostrar que el círculo está determinado de manera única por el triángulo.
Problema 4.7 Encontrar el semicírculo correcto
Un triángulo determina de manera única su círculo circunscrito (Problema 4.6). Sin embargo, es posible que el diámetro del círculo no se alinee con un lado del triángulo. ¿Se puede circunscribir siempre un semicírculo alrededor de un triángulo rectángulo mientras se alinea el diámetro del círculo a lo largo de la hipotenusa?
Problema 4.8 Media geométrica de tres números
Para tres números no negativos, la desigualdad AM—GM es
\[\frac{a + b + c}{3} \geqslant (abc)^{1/3}. \label{4.17} \]
¿Por qué es poco probable que esta desigualdad, a diferencia de su primo número dos, tenga una prueba geométrica? (Si encuentra una prueba, hágamelo saber.)
Aplicaciones
Las medias aritméticas y geométricas tienen una amplia aplicación matemática. La primera aplicación es un problema que más a menudo se resuelve con derivados: Doblar una longitud fija de barda en un rectángulo que encierra el jardín más grande.
¿Qué forma de rectángulo maximiza el área?
El problema involucra dos cantidades: un perímetro que es fijo y un área a maximizar. Si el perímetro está relacionado con la media aritmética y el área con la media geométrica, entonces la desigualdad AM—GM podría ayudar a maximizar el área. El perímetro\(P = 2(a + b)\) es cuatro veces la media aritmética, y el área\(A = ab\) es el cuadrado de la media geométrica. Por lo tanto, a partir de la desigualdad AM—GM,
\[\underbrace{\frac{P}{4}}_{\text{ AM }} \geqslant \underbrace{\sqrt{A}}_{\text{ GM }} \label{4.18} \]
con igualdad cuando\(a = b\). El lado izquierdo se fija por la cantidad de barda. Así el lado derecho, que varía según\(a\) y\(b\), tiene un máximo de\(P/4\) cuándo\(a = b\). El rectángulo de área máxima es un cuadrado.
Problema 4.9 Prueba pictórica directa
El razonamiento AM—GM para el jardín rectangular máximo es el razonamiento pictórico indirecto. Es un razonamiento simbólico construido sobre la prueba pictórica de la desigualdad AM- GM. ¿Se puede dibujar una imagen para mostrar directamente que el cuadrado es la forma óptima?
Problema 4.10 Producto de tres partes
Encuentra el valor máximo de\(f(x) = x^{2}(1 − 2x)\) for\(x \geqslant 0\), sin usar cálculo. Sketch\(f(x)\) para confirmar tu respuesta.
Problema 4.11 Área máxima sin restricciones
Si el jardín no necesita ser rectangular, ¿cuál es la forma de área máxima?
Problema 4.12 Maximización de volumen
Construya una caja abierta con la parte superior de la siguiente manera: Comience con un cuadrado unitario, corte cuatro esquinas idénticas y doble las solapas.
La caja tiene volumen\(V = x(1 − 2x)^{2}\), donde x es la longitud lateral de un recorte de esquina. ¿Qué elección de x maximiza el volumen de la caja?
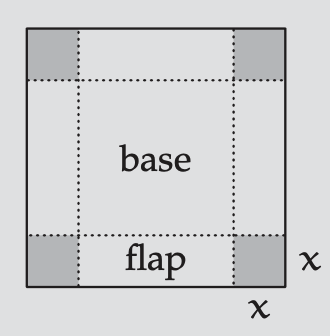
Aquí hay un análisis plausible modelado a partir del análisis del jardín rectangular. Establecer\(a = x\),\(b = 1 − 2x\), y\(c = 1 − 2x\). Entonces abc es el volumen V, y\(V^{1/3} = ^{3}\sqrt{abc}\) es la media geométrica (Problema 4.8). Porque la media geométrica nunca supera la media aritmética y porque las dos medias son iguales cuando\(a = b = c\), el volumen máximo se alcanza cuando\(x = 1 − 2x\). Por lo tanto, elegir\(x = 1/3\) debe maximizar el volumen de la caja.
Ahora demuestre que esta elección es incorrecta al graficar\(V(x)\) o establecer\(dV/dx = 0\); explicar lo que está mal con el razonamiento anterior; y hacer una versión correcta.
Problema 4.13 Mínimo trigonométrico
Encuentra el valor mínimo de
\[\frac{9x^{2} \sin^{2}x + 4}{x \sin x} \label{4.19} \]
en la región x\(\in\) (0,\(\pi\)).
Problema 4.14 Máximo trigonométrico
En la región t\(\in\) [0,\(\pi/2\)], maximizar\(\sin 2 t\) o, equivalentemente, 2\(\sin t \cos t\).
La segunda aplicación de las medias aritméticas y geométricas es un método moderno e increíblemente rápido para la computación\(\pi\) [5, 6]. Los métodos antiguos para calcular π incluían calcular el perímetro de polígonos regulares de muchos lados y proporcionaban algunos decimales de precisión.
Cálculos recientes han utilizado la serie arcangente de Leibniz
Imagina que quieres calcular π a\(10^{9}\) dígitos, tal vez para probar el hardware de una nueva supercomputadora o para estudiar si los dígitos de π son aleatorios (un tema en la novela de Carl Sagan Contact [40]). \(x = 1\)Ambientado en la serie Leibniz produce\(\pi/4\), pero la serie converge extremadamente lentamente. La obtención de\(10^{9}\) dígitos requiere\(10^{10^{9}}\) aproximadamente términos, mucho más términos que átomos en el universo.
Afortunadamente, una sorprendente identidad trigonométrica debida a John Machin (1686 — 1751) acelera la convergencia al reducir\(x\):
Incluso con la aceleración, la precisión\(10^{9}\) de los dígitos requiere calcular aproximadamente\(10^{9}\) términos.
En contraste, el algoritmo Brent—Salamin moderno [3, 41], que se basa en medias aritméticas y geométricas, converge a π extremadamente rápidamente. El algoritmo está estrechamente relacionado con métodos asombrosamente precisos para calcular el perímetro de una elipse (Problema 4.15) y también para calcular la inductancia mutua [23]. El algoritmo genera varias secuencias comenzando con\(a_{0}\) = 1 y\(g_{0}\) = 1/\(\sqrt{2}\); luego calcula las medias aritméticas sucesivas\(a_{n}\), las medias\(g_{n}\) geométricas y sus diferencias al cuadrado\(d_{n}\).
\[a_{n+1}=\frac{a_{n}+g_{n}}{2}, \quad g_{n+1}=\sqrt{a_{n} g_{n}}, \quad d_{n}=a_{n}^{2}-g_{n}^{2} \label{4.23} \]
Las secuencias a y g convergen rápidamente a un número M (\(a_{0}\),\(g_{0}\)) llamado la media aritmética-geométrica de\(a_{0}\) y\(g_{0}\). Entonces M (\(a_{0}\),\(g_{0}\)) y la secuencia de diferencia d determinan π.
\[\pi=\frac{4 M\left(a_{0}, g_{0}\right)^{2}}{1-\sum_{j=1}^{\infty} 2^{j+1} d_{j}} \label{4.24} \]
La secuencia d se aproxima a cero cuadráticamente; es decir,\(d_{n+1}\) ∼\(d^{2}_{n}\) (Problema 4.16). Por lo tanto, cada iteración en este cálculo de π duplica los dígitos de precisión. Un cálculo de mil millones de dígitos de π requiere solo alrededor de 30 iteraciones mucho menos que los 10109 términos que utilizan la serie arcotangente con\(x = 1\) o incluso que los\(10^{9}\) términos que usan la aceleración de Machin.
Problema 4.15 Perímetro de una elipse
Para calcular el perímetro de una elipse con eje semimajor\(a_{0}\) y eje semiminor\(g_{0}\), computar las secuencias a, g, y d y el límite común M (\(a_{0}, g_{0})\)de las secuencias a y g, como para el cálculo de\(\pi\). Entonces el perímetro P se puede calcular con la siguiente fórmula:
\[P=\frac{A}{M\left(a_{0}, g_{0}\right)}\left(a_{0}^{2}-B \sum_{j=0}^{\infty} 2^{j} d_{j}\right)\label{4.25} \]
donde A y B son constantes para que usted determine. Utilizar el método de casos fáciles (Capítulo 2) para determinar sus valores. (Consulte [3] para verificar sus valores y para obtener una prueba de la fórmula completada.)
Problema 4.16 Convergencia cuadrática
Comience con\(a_{0} = 1\) y\(g_{0} = 1/\sqrt{2}\) (o cualquier otro par positivo) y siga varias iteraciones de la secuencia AM—GM
\[a_{n + 1} = \frac{a_{n}+ g_{n}}{2} \text{ and } g_{n + 1} = \sqrt{a_{n}g_{n}}. \label{4.26} \]
Después generar\(d_{n} = a^{2}n − g^{2}n\) y\(log_{10}\) dn para verificar eso\(d_{n+1} ∼ d^{2}_{n}\) (convergencia cuadrática).
Problema 4.17 Rapidez de convergencia
Elija un positivo\(x_{0}\); luego genere una secuencia por la iteración
\[x_{n + 1} = \frac{1}{2}(x_{n} + \frac{2}{x_{n}}) (n \geqslant 0) \label{4.27} \]
¿A qué y con qué rapidez converge la secuencia? ¿Y si\(x_{0} < 0\)?


