4.5: Sumando serie
- Page ID
- 112465
Para el último ejemplo de lo que las imágenes pueden explicar, volver a la función factorial. Nuestra primera aproximación a n! comenzó con su representación integral y luego utilizó la formación de grumos (Sección 3.2.3).
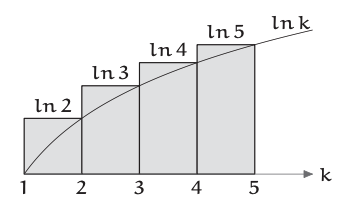
El agrupamiento, al reemplazar una curva por un rectángulo cuya área se calcula fácilmente, ya es un análisis pictórico. Una segunda foto para n! comienza con la representación sumatoria
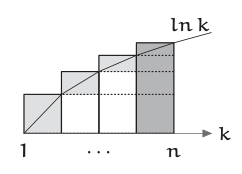
\[ln n! = \sum{1}^{n} lnK. \label{4.45} \]
Esta suma es igual al área combinada de los rectángulos circunscritos.
Establecer la altura de los rectángulos requiere dibujar la\(lnk\) curva que podría intersectar el borde superior de cada rectángulo en cualquier lugar a lo largo del borde. En la figura anterior y el análisis de esta sección, la curva se cruza en el punto final derecho del borde. Después de leer la sección, rehacer el análisis para otros dos casos:
a. La curva se cruza en el extremo izquierdo del borde.
b. La curva se cruza en el punto medio del borde.
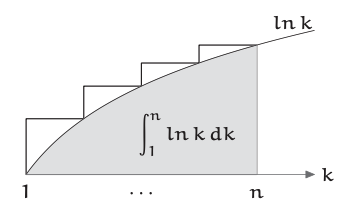
Esa área combinada es aproximadamente el área bajo la\(lnk\) curva, por lo que
\[ln n! ≈ \int_{1}^{n} ln k dk = n lnn - n + 1. \label{4.46} \]
¡Cada término en este\(lnn\)! aproximación aporta un factor a n! :
\[n! ≈ n^{n} x e^{-n} x e. \label{4.47} \]
Cada factor tiene una contraparte en un factor de la aproximación de Stirling (Sección 3.2.3). En orden descendente de importancia, los factores en la aproximación de Stirling son
\[n! ≈ n^{n} x e^{-n} x \sqrt{n} x \sqrt{2\pi}. \label{4.48} \]
La aproximación integral reproduce los dos factores más importantes y casi reproduce el cuarto factor: e y\(\sqrt{2π}\) difieren solo en 8%. El único factor inexplicable es\(\sqrt{n}\).
¿De dónde viene el\(\sqrt{n}\) factor?
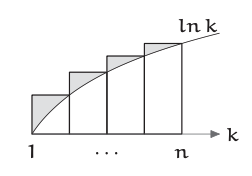
El\(\sqrt{n}\) factor debe provenir de los fragmentos por encima de la\(lnk\) curva. Son casi triángulos y sería más fácil de agregar si fueran triángulos. Por lo tanto, vuelva a dibujar la\(lnk\) curva usando segmentos de línea recta (otro uso de la formación de grumos).
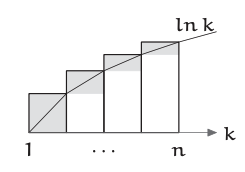
Los triángulos resultantes serían más fáciles de agregar si fueran rectángulos. Por lo tanto, dupliquemos cada triángulo para convertirlo en un rectángulo.
¿Cuál es la suma de estas piezas rectangulares?
Para sumar estas piezas, coloca tu mano derecha a lo largo de la línea\(k = n\) vertical. Con tu mano izquierda, mete las piezas hacia la derecha hasta que golpeen tu mano derecha. Las piezas luego se apilan para formar el\(lnn\) rectángulo. Debido a que cada pieza es el doble de la protuberancia triangular correspondiente, las protuberancias triangulares se suman a\((lnn)/2\). Esta corrección del triángulo mejora la aproximación integral. La aproximación resultante para ln n! ahora tiene un término más:
\[lnn n! ≈ \underbrace{nlnn - n + 1}_{\text{integral}} + \underbrace{\frac{lnn}{2}}_{\text{triangles}} \label{4.49} \]
Al exponenciar para obtener n! , la corrección aporta un factor de\(\sqrt{n}\).
\[n! ≈ n^{n} x e^{-n} x e x \sqrt{n}. \label{4.50} \]
En comparación con la aproximación de Stirling, la única diferencia restante es el factor de e que debería ser\(2\pi\), un error de solo 8% todo por hacer una integral y dibujar algunas imágenes.
Problema 4.31 ¿Subestimar o sobreestimar?
¿La aproximación integral con la corrección del triángulo subestima o sobreestima n!? Utilice el razonamiento pictórico; luego verifique la conclusión numéricamente.
Problema 4.32 Siguiente corrección
La corrección del triángulo es la primera de una serie infinita de correcciones. Las correcciones incluyen términos proporcionales a\(n − 2, n − 3\),..., y son difíciles de derivar usando solo imágenes. Pero la\(n − 1\) corrección se puede derivar con imágenes.
a. Dibuje las regiones que muestran el error cometido reemplazando la curva lisa ln k por una curva lineal por tramos (una curva compuesta por segmentos rectos).
b. Cada región está delimitada arriba por una curva que es casi una parábola, cuya área viene dada por la fórmula de Arquímedes (Problema 4.34)
\[\text{area} = \frac{2}{3} x \text{area of the circumscribing rectangle}. \label{4.51} \]
Utilizar la propoerdad para aproximar el área de cada región.
c. Demostrar que al evaluar\(ln n! = \sum_{1}^{n}\)\(ln k\), estas regiones suman aproximadamente\((1 − n^{−1})/12\).
d. ¿Cuál es el término constante resultante, mejorado (anteriormente e) en la aproximación a n! y ¿qué tan cerca está\(2\pi\)? ¿Qué factor contribuye el\(n − 1\) término en\(ln n!\) la aproximación a la n! aproximación?
Estas y posteriores correcciones se derivan en la Sección 6.3.2 utilizando la técnica de analogía.

