6.1: Trigonometría Espacial-El Ángulo de Enlace en Metano
- Page ID
- 112608
Cuando las cosas se ponen duras, los duros bajan sus estándares. Esta idea, tema de todo el libro, subyace a la última herramienta de razonamiento por analogía en la calle. Su consejo es sencillo: Ante un problema difícil, construya y resuelva un problema similar pero más simple, un problema análogo. La práctica desarrolla fluidez. La herramienta se introduce en la trigonometría espacial (Sección 6.1); se agudiza sobre la geometría sólida y la topología (Sección 6.2); luego se aplica a las matemáticas discretas (Sección 6.3) y, en el ejemplo de despedida, a una suma trascendental infinita (Sección 6.4).
Trigonometría espacial: El ángulo de unión en metano
La primera analogía proviene de la trigonometría espacial. En el metano (fórmula química\(CH^{4}\)), un átomo de carbono se encuentra en el centro de un tetraedro regular, y un átomo de hidrógeno se encuentra en cada vértice. ¿Cuál es el ángulo θ entre dos enlaces carbono-hidrógeno?
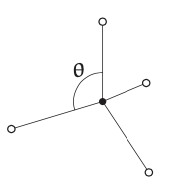
Los ángulos en tres dimensiones son difíciles de visualizar. Intenta, por ejemplo, imaginar y calcular el ángulo entre dos caras de un tetraedro regular. Debido a que los ángulos bidimensionales son fáciles de visualizar, construyamos y analicemos una molécula plana análoga. Conocer su ángulo de unión podría ayudarnos a adivinar el ángulo de unión del metano.
¿Debe la molécula planar análoga tener cuatro o tres hidrógenos?
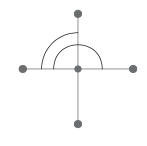
Cuatro hidrógenos producen cuatro enlaces que, cuando se separan regularmente en un plano, producen dos ángulos de enlace diferentes. Por el contrario, el metano contiene solo un ángulo de unión. Por lo tanto, el uso de cuatro hidrógenos altera una característica crucial del problema original. La solución probable es construir la molécula plana análoga usando solo tres hidrógenos.
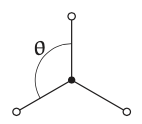
Tres hidrógenos dispuestos regularmente en un plano crean solo un ángulo de unión:\(θ = 120^{◦}\). ¡Quizás este ángulo sea el ángulo de unión en metano! Un punto de datos, sin embargo, es una caña delgada sobre la que colgar una predicción para dimensiones más altas. El punto de datos único para dos dimensiones (\(d = 2\)) es consistente con numerosas conjeturas, por ejemplo, que en d dimensiones el ángulo de unión es\(120^{◦}\)\((60d)^{◦}\) o mucho más.
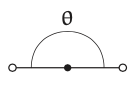
Seleccionar una conjetura razonable requiere recopilar más datos. Los datos fácilmente disponibles provienen de un problema aún más simple pero análogo: la molécula unidimensional y lineal\(CH_{2}\). Sus dos hidrógenos se encuentran uno frente al otro, por lo que los dos enlaces C—H forman un ángulo de\(θ = 180^{◦}\).
Con base en los datos acumulados, ¿cuáles son las conjeturas razonables para el ángulo tridimensional\(θ_{3}\)?
La molécula unidimensional elimina la conjetura de que\(θ_{d} = (60d)^{◦}\). También sugiere nuevas conjeturas por ejemplo, eso\(θ_{d} = (240 − 60d)^{◦}\) o\(θ_{d} = 360^{◦}/(d + 1)\). Probar estas conjeturas es una tarea ideal para el método de casos fáciles. La prueba de casos fáciles de dimensiones superiores (alta d) refuta la conjetura de que\(θ_{d} = (240 − 60d)^{◦}\). Para d alta, predice ángulos de unión inverosímiles, es decir,\(θ = 0\) para\(d = 4\) y\(θ < 0\) para\(d > 4\).
Afortunadamente, la segunda sugerencia,\(θ_{d} = 360^{◦}/(d + 1)\), pasa la misma prueba de casos fáciles. Sigamos probándolo evaluando su predicción para metano a saber,\(θ_{3} = 90^{◦}\). Imagínese entonces un hermano mayor del metano: una\(CH_{6}\) molécula con carbono en el centro de un cubo y seis hidrógenos en los centros faciales. Su pequeño ángulo de unión es\(90^{◦}\). (El otro ángulo de unión es\(180^{◦}\).) Ahora retire dos hidrógenos para\(CH_{6}\) convertirlos en\(CH_{4}\), extendiendo uniformemente los cuatro hidrógenos restantes. Reducir el hacinamiento eleva el pequeño ángulo de unión por encima\(90^{◦}\) y refuta la predicción de que\(θ_{3} = 90^{◦}\).
¿Cuántos hidrógenos se necesitan en los problemas análogos de ángulo de unión de cuatro y cinco dimensiones? Usa esta información para demostrarlo\(θ_{4} > 90^{◦}\). Es\(θ_{d} > 90^{◦}\). ¿para todos\(d\)?
Los datos hasta el momento han refutado las conjeturas de función racional más simples\((240 − 60d)^{◦}\) y\(360^{◦}/(d+1)\). Aunque otras conjeturas de función racional podrían sobrevivir, con solo dos puntos de datos las posibilidades son demasiado amplias. Peor aún, θd podría ni siquiera ser una función racional de d.
El progreso requiere una nueva idea: El ángulo de unión podría no ser la variable más simple de estudiar. Una dificultad análoga surge al conjeturar el siguiente término en las series 3, 5, 11, 29,...
¿Cuál es el siguiente término de la serie?
A primera vista, los números parecen casi aleatorios. Sin embargo, restar 2 de cada término produce 1, 3, 9, 27,... Así, en la serie original es probable que el siguiente término sea 83. Del mismo modo, una simple transformación de los\(θ_{d}\) datos podría ayudarnos a conjeturar un patrón para\(θ_{d}\).
¿Qué transformación de los\(θ_{d}\) datos produce patrones simples?
La transformación deseada debe producir patrones simples y tener justificación estética o lógica. Una justificación es la estructura de un cálculo honesto del ángulo de unión, que puede calcularse como un producto de punto de dos vectores C—H (Problema 6.3). Debido a que los productos dot involucran cosenos, una transformación que vale la pena\(θ_{d}\) es\(\cos θ_{d}\).

Esta transformación simplifica los datos: La\(\cos θ_{d}\) serie comienza simplemente −1, −1/2,. Dos continuaciones plausibles son −1/4 o −1/3; corresponden, respectivamente, al término general\(−1/2^{d−1}\) o\(−1/d\).
¿Qué continuación y conjetura es la más plausible?
Ambas conjeturas predicen\(\cos θ < 0\) y por lo tanto\(θ_{d} > 90^{◦}\) (para todos\(d\)). Esta predicción compartida es alentadora (Problema 6.1); sin embargo, ser compartida significa que no distingue entre las conjeturas.
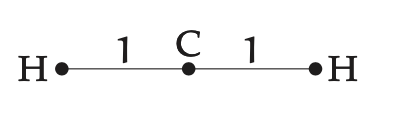
¿Alguno conjetura matemática la geometría molecular? Una característica geométrica importante, aparte del ángulo de unión, es la posición del carbono. En una dimensión, se encuentra a medio camino entre los dos hidrógenos, por lo que divide el segmento de línea H—H en dos piezas que tienen una relación de longitud 1:1.
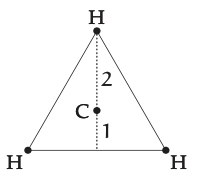
En dos dimensiones, el carbono se encuentra en la altitud que conecta un hidrógeno con el punto medio de los otros dos hidrógenos. El carbono divide la altitud en dos piezas que tienen una relación de longitud 1:2.
¿Cómo divide el carbono la altitud análoga del metano?
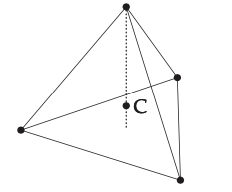
En metano, la altitud análoga va desde el vértice superior hasta el centro de la base. El carbono se encuentra en la posición media y por lo tanto en la altura media de los cuatro hidrógenos. Debido a que los tres hidrógenos base tienen altura cero, la altura media de los cuatro hidrógenos es h/4, donde h es la altura del hidrógeno superior. Así, en tres dimensiones, el carbono divide la altitud en dos partes que tienen una relación de longitud de\(h/4 : 3h/4\) o 1:3. En dimensiones d, por lo tanto, el carbono probablemente divide la altitud en dos partes que tienen una relación de longitud de\(1:d\) (Problema 6.2).
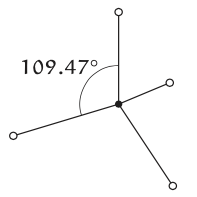
Debido a que\(1 : d\) surge naturalmente en la geometría,\(\cos θ_{d}\) es más probable que contenga\(1/d\) en lugar de\(1/2^{d - 1}\). Así, lo más parecido de las dos\(\cos θ_{d}\) conjeturas es que
\[cosθ_{d} = -\frac{1}{d}. \label{6.1} \]
Para el metano, donde\(d = 3\), el ángulo de enlace previsto es\(\arccos(−1/3)\) o aproximadamente\(109.47^{◦}\). Esta predicción usando razonamiento por analogía concuerda con el experimento y con un cálculo honesto usando geometría analítica (Problema 6.3).
Problema 6.2 Posición de Carbon en dimensiones más altas
Justificar la conjetura de que el carbono divide la altitud en dos pedazos que tienen una relación de longitud\(1 : d\).
Problema 6.3 Solución de geometría analítica
Para verificar la solución usando analogía, use la geometría analítica de la siguiente manera para encontrar el ángulo de unión. Primero, asigne coordenadas (\(x_{n}\),\(y_{n}\),\(z_{n}\)) a los\(n\) hidrógenos, donde\(n = 1 . . . 4\), y resuelva para esas coordenadas. (Usa la simetría para hacer que las coordenadas sean lo más simples que puedas). Luego elige dos vectores C—H y calcula el ángulo que subtienden.
Problema 6.4 Caso extremo de alta dimensionalidad
Dibuja una imagen para explicar la aproximación de ángulo pequeño\(\arccos x ≈ \pi/2 − x\). ¿Cuál es el ángulo de unión aproximado en dimensiones altas (grandes\(d\))? ¿Puedes encontrar una explicación intuitiva para el ángulo de unión aproximado?


