6.2: Topología- Cuántas regiones
- Page ID
- 112609
El ángulo de unión en metano (Sección 6.1) se puede calcular directamente con geometría analítica (Problema 6.3), por lo que el razonamiento por analogía no muestra toda su potencia. Por lo tanto, intente el siguiente problema.
¿En cuántas regiones dividen cinco planos el espacio?
Esta formulación permite arreglos degenerados como cinco planos paralelos, cuatro planos que se encuentran en un punto o tres planos que se encuentran en una línea. Para eliminar estas y otras degeneraciones, coloquemos y orientemos los planos al azar, maximizando así el número de regiones. El problema es entonces encontrar el número máximo de regiones producidas por cinco planos.

Cinco planos son difíciles de imaginar, pero el método de casos fáciles usando menos planos podría producir un patrón que generalice a cinco planos. El caso más fácil es cero planos: El espacio permanece entero así\(R(0) = 1\) (donde R (n) denota el número de regiones producidas por n planos). El primer plano divide el espacio en dos mitades, dando\(R(1) = 2\). Para agregar el segundo plano, imagina cortar una naranja dos veces para producir cuatro gajos:\(R(2) = 4\).
¿Qué patrón (s) aparecen en los datos?
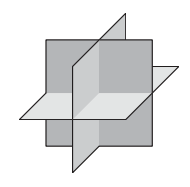
Una conjetura razonable es esa\(R(n) = 2^{n}\). Para probarlo, prueba el caso\(n = 3\) cortando la naranja por tercera vez y cortando cada una de las cuatro piezas en dos trozos más pequeños; así, efectivamente\(R(3)\) es 8. Quizás el patrón continúa con\(R(4) = 16\) y\(R(5) = 32\). En la siguiente tabla para\(R(n)\), estas dos extrapolaciones están marcadas en gris para distinguirlas de las entradas verificadas.
| n | 0 | 1 | 2 | 3 | 4 | 5 |
| r | 1 | 2 | 4 | 8 | 16 | 32 |
¿Cómo se puede probar más la\(R(n) = 2^{n}\) conjetura?
Una prueba directa contando regiones es difícil porque las regiones son difíciles de visualizar en tres dimensiones. Un problema bidimensional análogo sería más fácil de resolver, y su solución puede ayudar a probar la conjetura tridimensional. Un espacio bidimensional está dividido por líneas, por lo que la pregunta análoga es la siguiente:
¿Cuál es el número máximo de regiones en las que n líneas dividen el plano?
El método de casos fáciles podría sugerir un patrón. Si el patrón es\(2^{n}\), entonces es probable que la\(R(n) = 2^{n}\) conjetura se aplique en tres dimensiones.
¿Qué sucede en unos pocos casos fáciles?
Las líneas cero dejan el avión entero, dando\(R(0) = 1\). Los siguientes tres casos son los siguientes (aunque ver Problema 6.5):
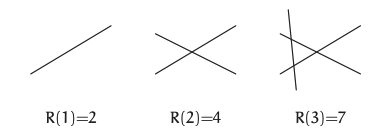
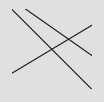
Problema 6.5 Tres líneas de nuevo
La\(R(3) = 7\) ilustración mostró tres líneas produciendo siete regiones. Aquí hay otro ejemplo con tres líneas, también en un arreglo aleatorio, pero parece producir sólo seis regiones. ¿Dónde, si en algún lugar, está la séptima región? ¿O es\(R(3) = 6\)?
Problema 6.6 Convexidad
¿Deben ser convexas todas las regiones creadas por las líneas? (Una región es convexa si y sólo si un segmento de línea que conecta dos puntos cualesquiera dentro de la región se encuentra completamente dentro de la región.) ¿Qué pasa con las regiones tridimensionales creadas al colocar planos en el espacio?
Hasta que\(R(3)\) resultó ser 7, la conjetura\(R(n) = 2^{n}\) se veía sólida. No obstante, antes de descartar una conjetura tan simple, dibuje una cuarta línea y cuente cuidadosamente las regiones. Cuatro líneas hacen solo 11 regiones en lugar de las 16 predichas, por lo que la\(2^{n}\) conjetura está muerta.
Una nueva conjetura podría surgir al ver los datos bidimensionales\(R_{2}(n)\) junto con los datos tridimensionales\(R_{3}(n)\).
| n | 0 | 1 | 2 | 3 | 4 |
| \(R_{2}\) | 1 | 2 | 4 | 7 | 11 |
| \(R_{3}\) | 1 | 2 | 4 | 8 |
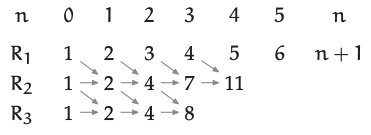
En esta tabla, se combinan varias entradas para hacer entradas cercanas. Por ejemplo,\(R_{2}(1)\) y\(R_{3}(1)\) las dos entradas en la\(n = 1\) columna suman a\(R_{2}(2)\) o\(R_{3}(2)\). Estas dos entradas a su vez suman a la\(R_{3}(3)\) entrada. Pero la tabla tiene muchos números pequeños con muchas formas de combinarlos; descartar las coincidencias requiere recopilar más datos y la fuente de datos más simple es el problema unidimensional análogo.
¿Cuál es el número máximo de segmentos en los que n puntos dividen una línea?
Una respuesta tentadora es que n puntos hacen n segmentos. Sin embargo, un caso fácil de que un punto produzca dos segmentos reduce la tentación. Más bien,\(n\) los puntos hacen\(n + 1\) segmentos. Ese resultado genera la\(R_{1}\) fila en la siguiente tabla.
| n | 0 | 1 | 2 | 3 | 4 | 5 | n |
| \(R_{1}\) | 1 | 2 | 3 | 4 | 5 | 6 | n + 1 |
| \(R_{2}\) | 1 | 2 | 4 | 7 | 11 | ||
| \(R_{3}\) | 1 | 2 | 4 | 8 |
¿Qué patrones hay en estos datos?
La conjetura 2n sobrevive parcialmente. En la\(R_{1}\) fila, falla a partir de\(n = 2\). En la\(R_{2}\) fila, falla a partir de\(n = 3\). Así, en la\(R_{3}\) fila, probablemente falla a partir de\(n = 4\), haciendo las conjeturas\(R_{3}\) (4) = 16 e\(R_{3}(5) = 32\) improbables. Mi estimación personal es que, antes de ver estos fracasos, la probabilidad de la\(R_{3}(4) = 16\) conjetura era de 0.5; pero ahora cae a lo sumo 0.01. (Para más información sobre la estimación y actualización de las probabilidades de conjeturas, vea los importantes trabajos sobre razonamiento plausible de Corfield [11], Jaynes [21] y Polya [36].)
En mejores noticias, las aparentes coincidencias contienen un patrón robusto:
Si el patrón continúa, ¿en cuántas regiones pueden cinco planos dividir el espacio?
Según el patrón,
\[R_{3}(4) = \underbrace{R_{2}(3)}_{7} + \underbrace{R_{3}(3)}_{8} = 15 \label{6.2} \]
y luego
\[R_{3}(5) = \underbrace{R_{2}(4)}_{11} + \underbrace{R_{3}(4)}_{15} = 26. \label{6.3} \]
Así, cinco planos pueden dividir el espacio en un máximo de 26 regiones.
Este número es difícil de deducir dibujando cinco planos y contando las regiones. Además, ese enfoque de fuerza bruta daría el valor de solo\(R_{3}\) (5), mientras que los casos fáciles y la analogía dan un método para computar cualquier entrada en la tabla. Con ello, proporcionan datos suficientes para conjeturar expresiones para\(R_{2}\) (n) (Problema 6.9), para\(R_{3}\) (n) (Problema 6.10) y para la entrada general\(R_{d}\) (n) (Problema 6.12).
Problema 6.7 Comprobación del patrón en dos dimensiones
El patrón conjeturado predice\(R_{2}(5) = 16\): que cinco líneas pueden dividir el plano en 16 regiones. Verifique la conjetura dibujando cinco líneas y contando las regiones.
Problema 6.8 Datos libres de dimensiones cero
Debido a que el problema unidimensional dio datos útiles, pruebe el problema de la dimensión cero. Extienda el patrón de las\(R_{1}\) filas\(R_{3}\)\(R_{2}\), y hacia arriba para construir una\(R_{0}\) fila. Da el número de regiones de dimensión cero (puntos) producidas dividiendo un punto con n objetos (de dimensión −1). ¿Qué pasa\(R_{0}\) si la fila va a seguir el patrón observado? ¿Ese resultado es consistente con el significado geométrico de tratar de subdividir un punto?
Problema 6.9 Resultado general en dos dimensiones
Los\(R_{0}\) datos se ajustan\(R_{0}(n) = 1\) (Problema 6.8), que es un polinomio de grado cero. Los\(R_{1}\) datos se ajustan\(R_{1}(n) = n + 1\), que es un polinomio de primer grado. Por lo tanto, los\(R_{2}\) datos probablemente se ajustan a una cuadrática.
Pruebe esta conjetura ajustando los datos\(n = 0 . . . 2\) a la cuadrática general\(An^{2} + Bn + C\), sacando repetidamente la gran parte (Capítulo 5) de la siguiente manera.
a. adivina un valor razonable para el coeficiente cuadrático A. Luego sacar (sub- tracto) la parte grande\(An^{2}\) y tabular lo sobrante,\(R^{2}(n) − An^{2}\), para\(n = 0 . . . 2\). Si el sobrante no es lineal en n, entonces queda un término cuadrático o se eliminó demasiado. En cualquier caso, ajuste A.
b. Una vez que el coeficiente cuadrático A sea correcto, utilice un procedimiento análogo para encontrar el coeficiente lineal B.
c. De igual manera resolver para el coeficiente constante C.
d. Verifique su ajuste cuadrático con nuevos datos (\(R_{2}(n)\)para\(n \geqslant 3\)).
Problema 6.10 Resultado general en tres dimensiones
Una conjetura razonable es que la\(R_{3}\) fila coincide con un cúbico (Problema 6.9). Usa sacar la parte grande para ajustar un cúbico a los\(n = 0 . . . 3\) datos. ¿Produce los valores conjeturados\(R_{3}(4) = 15\) y\(R_{3}(5) = 26\)?
Problema 6.11 Explicación geométrica
Encuentra una explicación geométrica para el patrón observado. Pista: Explica primero por qué el patrón genera la\(R_{2}\) fila a partir de la\(R_{1}\) fila; luego generaliza la razón para explicar la\(R_{3}\) fila.
Problema 6.12 Solución general en dimensión arbitraria
El patrón que conecta las entradas vecinas de la\(R_{d}(n)\) tabla es el patrón que genera el triángulo de Pascal [17]. Debido a que el triángulo de Pascal produce coeficientes binomiales, la expresión general\(R_{d}(n)\) debe contener coeficientes binomiales.
Por lo tanto, utilice coeficientes binomiales para expresar\(R_{0}(n)\) (Problema 6.8),\(R_{1}\) (n), y\(R_{2}\) (n) (Problema 6.9). Después conjeturar una forma de coeficiente binomio para\(R_{3}\) (n) y\(R_{d}\) (n), comprobando el resultado contra Problema 6.10.
Problema 6.13 Conjetura Power-of-2
Nuestra primera conjetura para el número de regiones fue\(R_{d}(n) = 2\). En tres dimensiones, funcionó hasta\(n = 4\).
En\(d\) dimensiones, mostrar eso\(R_{d}(n) = 2^{n}\) para\(n \leqslant d\) (quizás usando los resultados del Problema 6.12).


