6.4: Raíces tangentes- Una suma trascendental desalentadora
- Page ID
- 112593
Nuestro ejemplo de despedida, elegido porque su análisis combina diversas herramientas de lucha callejera, es una difícil suma infinita.
\(\text{Find} S ≡ \sum x_{n}^{-2} \text{ where the } x_{n} \text{ are the positive solutions of } \tan x = x\)
Las soluciones\(\tan x = x\) o, equivalentemente, las raíces de\(\tan x − x\), son trascendentales y no tienen forma cerrada, sin embargo, se requiere una forma cerrada para casi todos los métodos de suma. Los métodos de lucha en la calle vendrán a nuestro rescate.
Fotos y estuches fáciles
Comience el análisis con un caso ojalá fácil.
¿Cuál es la primera raíz\(x_{1}\)?
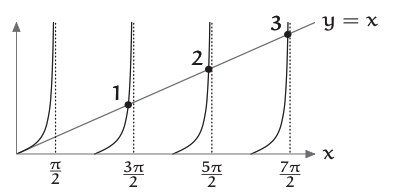
Las raíces de\(\tan x − x\) están dadas por las intersecciones de\(y = x\) y\(y = \tan x\). Sorprendentemente, no se produce intersección en la rama de\(\tan x\) donde\(0 < x < \pi/2\) (Problema 6.23); la primera intersección es justo antes de la asíntota en\(x = 3\pi/2\). Así,\(x_{1} ≈ 3\pi/2\).
Mostrar simbólicamente que no\(\tan x = x\) tiene solución para\(0 < x < \pi/2\). (El resultado parece plausible pictóricamente pero vale la pena comprobarlo para poder dibujar el cuadro).
¿Dónde, aproximadamente, están las intersecciones posteriores?
\(x\)A medida que crece, la\(y = x\) línea cruza la\(y = \tan x\) gráfica cada vez más arriba y por lo tanto cada vez más cerca de las asíntotas verticales. Por lo tanto, realice la siguiente aproximación de asíntota para la gran parte de\(x_{n}\):
\[x_{n} ≈ (n + \frac{1}{2})\pi. \label{6.18} \]
Sacando la gran parte
Esta expresión aproximada de baja entropía para\(x_{n}\) da la gran parte de\(S\) (la aproximación cero).
\[S ≈ \sum[\underbrace{(n + \frac{1}{2}\pi}_{≈x_{n}}]^{-2} = \frac{4}{\pi^{2}} \sum_{1}^{\infty} \frac{1}{(2n + 1)^{2}}. \label{6.19} \]
La suma\(\sum_{1}^{\infty} (2n + 1)^{−2}\) es, a partir de una imagen (Sección 4.5) o de la suma de Euler-Maclaurin (Sección 6.3.2), aproximadamente la siguiente integral.
\[\sum_{1}^{\infty}(2n + 1)^{-2} \approx \int_{1}^{\infty}(2n+1)^{-2} \mathrm{~d} n=-\frac{1}{2} \times\left.\frac{1}{2n + 1}\right|_{1} ^{\infty}=\frac{1}{6}\label{6.20} \]
Por lo tanto,
\[S ≈ \frac{4}{\pi^{2}} x \frac{1}{6} = 0.067547... \label{6.21} \]
Las protuberancias sombreadas son aproximadamente triángulos, y suman la mitad del primer rectángulo. Ese rectángulo tiene área 1/9, entonces
\[\sum_{1}^{\infty} (2n + 1)^{-2} ≈ \frac{1}{6} + \frac{1}{2} x \frac{1}{9} = \frac{2}{9}. \label{6.22} \]
Por lo tanto, una estimación más precisa de\(S\) es
\[S ≈ \frac{4}{\pi^{2}} x \frac{2}{9} = 0.090063..., \label{6.23} \]
que es ligeramente superior a la primera estimación.
¿La nueva aproximación es una sobreestimación o una subestimación?
La nueva aproximación se basa en dos subestimaciones. Primero, la aproximación de la asíntota\(x_{n} ≈ (n + 0.5)\pi\) sobreestima cada xn y por lo tanto subestima los recíprocos cuadrados en la suma\(\sum x_{n}^{-2}\). Segundo, después de hacer la aproximación de la asíntota, la aproximación pictórica a la suma\(\sum_{1}^{\infty}(2n + 1)^{−2}\) reemplaza cada protuberancia con un triángulo inscrito y con ello subestima cada protuberancia (Problema 6.24).
Dibuja una imagen de la subestimación en la aproximación pictórica
\[\int_{1}^{\infty} \frac{1}{(2n + 1)^{2}} ≈ \frac{1}{6} + \frac{1}{2} x \frac{1}{9}. \label{6.24} \]
¿Cómo se pueden remediar estas dos subestimaciones?
La segunda subestimación (las protuberancias) se elimina sumando\(\sum_{1}^{\infty} (2n + 1)^{−2}\) exactamente. La suma es desconocida en parte porque su primer término es la fracción 1/9 cuya arbitrariedad aumenta la entropía de la suma. Incluyendo el\(n = 0\) término, que es 1, y los recíprocos igualados al cuadrado\(1/(2n)^{2}\) produce una suma compacta y familiar de menor entropía.
\[\int_{1}^{\infty} \frac{1}{(2n + 1)^{2}} + 1 + \int_{1}^{\infty} \frac{1}{(2n)^{2}} = \int_{1}^{\infty} \frac{1}{n^{2}}. \label{6.25} \]
La suma final de baja entropía es la famosa suma de Basilea (los resultados de alta entropía no suelen ser famosos). Su valor es\(B = \pi^{2}/6\) (Problema 6.22).
¿Cómo\(B = \pi^{2}/6\) ayuda saber a evaluar la suma original\(\sum_{1}^{\infty} (2n + 1)^{−2}\)?
La mayor modificación con respecto a la suma original fue incluir los recíprocos igualados al cuadrado. Su suma es\(B/4\).
\[\sum_{1}^{\infty} \frac{1}{(2n)^{2}} = \frac{1}{4} \sum_{1}^{\infty} \frac{1}{n^{2}}. \label{6.26} \]
La segunda modificación consistió en incluir el\(n = 0\) término. Así, para obtener\(\sum_{1}^{\infty} (2n + 1)^{−2}\), ajustar el valor de Basilea\(B\) restando\(B/4\) y luego el\(n = 0\) término. El resultado, después de sustituir\(B = \pi^{2}/6\), es
\[\sum_{1}^{\infty} \frac{1}{(2n + 1)^{2}} = B - \frac{1}{4}B - 1 = \frac{\pi^{2}}{8} - 1 \label{6.27} \]
Esta suma exacta, con base en la aproximación de asíntota para\(x_{n}\), produce la siguiente estimación de\(S\).
\[S ≈ \frac{4}{\pi^{2}} \sum_{1}^{\infty} \frac{1}{(2n + 1)^{2}} = \frac{4}{\pi^{2}} (\frac{\pi^{2}}{8} - 1) \label{6.28} \]
Simplificar al expandir el producto da
\[S ≈ \frac{1}{2} - \frac{4}{pi^{2}} = 0.094715... \label{6.29} \]
Revisa el razonamiento pictórico anterior (Problema 6.24) que\(1/6 + 1/18 = 2/9\) subestima\(\sum_{1}^{\infty} (2n + 1)^{−2}\). ¿Qué tan precisa fue esa estimación?
Esta estimación de\(S\) es la tercera que utiliza la aproximación de asíntota\(x_{n} ≈ (n + 0.5)\pi\). Ensamblados juntos, las estimaciones son
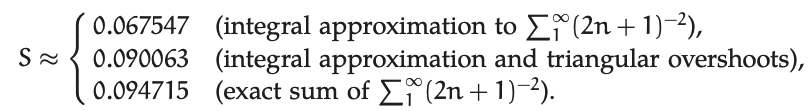
Debido a que la tercera estimación incorporó el valor exacto de\(\sum_{1}^{\infty} (2n + 1)^{−2}\), cualquier error restante en la estimación de\(S\) debe pertenecer a la propia aproximación de la asíntota.
¿Para qué término de\(\sum {x_{n}}^{−2}\) la aproximación de la asíntota es más inexacta?
\(x\)A medida que crece, las gráficas\(x\) y se\(\tan x\) cruzan cada vez más cerca de la asíntota vertical. Así, la aproximación de la asíntota hace su mayor error absoluto cuando\(n = 1\). Debido a que\(x_{1}\) es la raíz más pequeña, el error fraccional en\(x_{n}\) es, relativo al error absoluto en\(x_{n}\), aún más concentrado en\(n = 1\). El error fraccional en\(x_{n}^{−2}\), siendo −2 veces el error fraccional\(n\) en\(x\) (Sección 5.3), se concentra igualmente en\(n = 1\). Debido a que\(x_{n}^{−2}\) es el más grande en\(n = 1\), el error absoluto en\(x_{n}^{−2}\) (el error fraccional multiplicado por\(x_{n}^{−2}\) sí mismo) es, con mucho, el más grande en\(n = 1\).
Estimar, en función de\(n\), el error absoluto en\(x_{n}^{−2}\) que se produce por la aproximación de la\(n\) asíntota.
Con el error tan concentrado en\(n = 1\), la mayor mejora en la estimación de\(S\) proviene de reemplazar la aproximación\(x_{1} = (n + 0.5)\pi\) por un valor más preciso. Un enfoque numérico simple es la aproximación sucesiva utilizando el método Newton—Raphson (Problema 4.38). Para encontrar una raíz con este método, hacer una suposición inicial\(x\) y mejorarla repetidamente usando el reemplazo
\[x \rightarrow x - \frac{\tan x - x}{\sec^{2}x - 1}. \label{6.30} \]
Cuando la suposición inicial para\(x\) está ligeramente por debajo de la primera asíntota en\(1.5\pi\) el procedimiento converge rápidamente a\(x_{1} = 4.4934 . . .\)
Por lo tanto, para mejorar la estimación\(S ≈ 0.094715\), que se basó en la aproximación de la asíntota, restar su primer término aproximado (su gran parte) y sumar el primer término corregido.
\[S = S_{\text{old}} - \frac{1}{(1.5\pi)^{2}} + \frac{1}{4.4934^{2}} ≈ 0.09921. \label{6.31} \]
Usando el método Newton—Raphson para refinar, además, el\(1/x_{2}^{2}\) término da\(S ≈ 0.09978\) (Problema 6.27). Por lo tanto, una suposición altamente educada es
\[S = \frac{1}{10}. \label{6.32} \]
¡La suma infinita de números trascendentales desconocidos no parece ser trascendental ni irracional! Este sencillo y sorprendente número racional merece una explicación sencilla.
Elige un pequeño\(N\), digamos 4. Luego use el método Newton—Raphson para calcular valores precisos de\(x_{n}\) for\(n = 1 . . . N\); y use esos valores para refinar la estimación de\(S\). A medida que extiende el cálculo a valores mayores de\(N\), ¿las estimaciones refinadas de\(S\) acercarse a nuestra conjetura educada de 1/10?
Analogía con polinomios
¡Si tan solo la ecuación\(\tan x − x = 0\) tuviera unas pocas soluciones de forma cerrada! Entonces la suma\(S\) sería fácil de calcular. Ese deseo se cumple\(\tan x − x\) reemplazando por una ecuación polinómica por raíces simples. El polinomio interesante más simple es el cuadrático, así que experimenta con una cuadrática simple por ejemplo,\(x^{2} − 3x + 2\).
Este polinomio tiene dos raíces,\(x = 1\) y\(x = 2\); por lo tanto\(\sum x_{n}^{−2}\), el análogo de suma polinomial-raíz de la suma tangente-raíz, tiene dos términos.
\[\sum x_{n}^{-2} = \frac{1}{1^{2}} + \frac{1}{2^{2}} = \frac{5}{4}. \label{6.33} \]
Este método de fuerza bruta para calcular la suma raíz requiere una solución a la ecuación cuadrática. Sin embargo, un método que pueda transferirse a la ecuación\(\tan x − x = 0\), que no tiene una solución de forma cerrada, no puede usar las raíces mismas. Debe utilizar únicamente las características superficiales de la cuadrática a saber, sus dos coeficientes 2 y −3. Desafortunadamente, ningún método plausible de combinar 2 y −3 predice eso\(\sum x_{n}^{−2} = 5/4\).
¿Dónde salió mal la analogía polinomial?
El problema es que la cuadrática no\(x^{2} − 3x + 2\) es suficientemente similar a\(\tan x − x\). El cuadrático solo tiene raíces positivas; sin embargo\(\tan x − x\),, una función impar, tiene raíces positivas y negativas simétricas y tiene una raíz en\(x = 0\). En efecto, la serie Taylor para\(\tan x\) es\(x + x^{3}/3 + 2x^{5}/15 + ···\) (Problema 6.28); por lo tanto,
\[\tan x - x = \frac{x^{3}}{3} + \frac{2x^{5}}{15} + ... \label{6.34} \]
El factor común de\(x^{3}\) medios que\(\tan x − x\) tiene una triple raíz en\(x = 0\).
Un polinomio análogo aquí, uno con una raíz triple en\(x = 0\), una raíz positiva y una raíz negativa simétrica es\((x+2) x^{3}(x−2)\) o, después de la expansión,\(x^{5} − 4x^{3}\). La suma\(\sum x_{n}\) (usando la raíz positiva) contiene solo un término y es simplemente 1/4. Este valor podría surgir de manera plausible como la relación (negativa) de los dos últimos coeficientes del polinomio.
Para decidir si ese patrón es una coincidencia, pruebe con un polinomio más rico: uno con raíces en −2, −1, 0 (triple), 1 y 2. Uno de esos polinomios es
\[(x + 2)(x + 1)x^{3}(x - 1)(x - 2) = x^{7} - 5x^{5} + 4x^{3}. \label{6.35} \]
La suma polinomio-raíz utiliza sólo las dos raíces positivas 1 y 2 y es\(1/1^{2} + 1/2^{2}\), que es 5/4 la relación (negativa) de los dos últimos coeficientes.
Como prueba final de este patrón, incluir −3 y 3 entre las raíces. El polinomio resultante es
\[(x^{7} - 5x^{5} +4x^{3}) (x + 3)(x - 3) = x^{9} - 14x^{7} + 49x^{5} - 36x^{3}. \label{6.36} \]
La suma de raíz polinómica utiliza las tres raíces positivas 1, 2 y 3 y es\(1/1^{2} + 1/2^{2} + 1/3^{2}\), que es 49/36 nuevamente la relación (negativa) de los dos últimos coeficientes en el polinomio expandido.
¿Cuál es el origen del patrón y cómo se puede extender\(\tan x − x\)?
Para explicar el patrón, ordene el polinomio de la siguiente manera:
\[x^{9} − 14x^{7} + 49x^{5} − 36x^{3} = −36x^{3} (1 - \frac{49}{36}x^{2} + \frac{14}{36}x^{4} - \frac{1}{36}x^{6}). \label{6.37} \]
En este arreglo, la suma 49/36 aparece como la negativa del primer coeficiente interesante. Vamos a generalizar. La colocación de\(k\) raíces en\(x = 0\) y raíces individuales en\(± x_{1}, ± x_{2}, . . ., ± x_{n}\) da el polinomio
\[Ax^{k}(1 - \frac{x^{2}}{x_{1}^{2}}) \frac{x^{2}}{x_{2}^{2}}) \frac{x^{2}}{x_{3}^{2}}) ... \frac{x^{2}}{x_{n}^{2}}), \label{6.38} \]
donde\(A\) es una constante. Al expandir el producto de los factores entre paréntesis, el coeficiente del\(x^{2}\) término en la expansión recibe una contribución de cada\(x^{2}/x_{k}^{2}\) término en un factor. Así, comienza la expansión
\[Ax^{k}[1 - (\frac{1}{x_{1}^{2}} + \frac{1}{x_{2}^{2}} + \frac{1}{x_{3}^{2}} + ... + \frac{1}{x_{n}^{2}})x^{2} + ...].\label{6.39} \]
El coeficiente\(x^{2}\) de entre paréntesis es\(\sum_{x_{n}}^{−2}\), que es el análogo polinómico de la suma tangente-raíz.
Apliquemos este método a\(\tan x − x\). Aunque no es un polinomio, su serie Taylor es como un polinomio de infinitos grados. La serie Taylor es
\[\frac{x^{3}}{3} + \frac{2x^{5}}{15} + \frac{17x^{7}}{315} + ... = \frac{x^{3}}{3} (1 + \frac{2}{5}x^{2} + \frac{17}{105}x^{4} + ...). \label{6.40} \]
El negativo del\(x^{2}\) coeficiente debe ser −\(\sum x_{n}^{-2}\). Para el problema de tangentsum, por lo tanto,\(x − 2\) debería ser −2/5. Desafortunadamente, ¡la suma de cantidades positivas no puede ser negativa!
¿Qué salió mal con la analogía?
Un problema es que\(\tan x − x\) podrían tener raíces imaginarias o complejas cuyos cuadrados aportan cantidades negativas a\(S\). Afortunadamente, todas sus raíces son reales (Problema 6.29). Un problema más difícil de resolver es que\(\tan x − x\) va al infinito en valores finitos de\(x\), y lo hace infinitamente a menudo, mientras que ningún polinomio lo hace ni una sola vez.
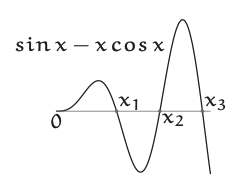
La solución es construir una función que no tenga infinidades pero que tenga las mismas raíces que\(\tan x − x\). Las infinidades de\(\tan x − x\) ocurren donde\(\tan x\) estalla, que es donde\(\cos x = 0\). Para eliminar las infinidades sin crear ni destruir raíces, multiplicar\(\tan x − x\) por\(\cos x\). La función polinómica para expandir es por lo tanto\(\sin x − x \cos x\).
Su expansión Taylor es
\[\underbrace{\left(x-\frac{x^{3}}{6}+\frac{x^{5}}{120}-\cdots\right)}_{\sin x}-\underbrace{\left(x-\frac{x^{3}}{2}+\frac{x^{5}}{24}-\cdots\right)}_{x \cos x} . \label{6.41} \]
La diferencia de las dos series es
\[\sin x - x\cos x = \frac{x^{3}}{3}(1 - \frac{1}{10}x^{2} + ...). \label{6.42} \]
El\(x^{3}/3\) factor indica la triple raíz en\(x = 0\). Y ahí por fin, como el negativo del\(x^{2}\) coeficiente, se asienta nuestra suma tangente-raíz\(S = 1/10\).
Problema 6.28 Serie Taylor para la tangente
Usa la serie Taylor para\(\sin x\) y\(\cos x\) para demostrarlo
\[tan x = x + \frac{x^{3}}{3} + \frac{2x^{5}}{15} + ... . \label{6.43} \]
Pista: Usa sacar la parte grande.
Problema 6.29 Solo raíces reales
Demuestre que todas las raíces de\(\tan x − x\) son reales.
Problema 6.30 Suma exacta de Basilea
Utilizar la analogía polinómica para evaluar la suma de Basilea
\[\sum_{1}^{\infty} \frac{1}{n^{2}} \label{6.44} \]
Compara tu resultado con tu solución a Problema 6.22.
Problema 6.31 Expansiones alternativas engañosas
Al cuadrar y tomar el recíproco de\(\tan x = x\) da\(cot^{2}x = x^{−2}\); equivalentemente,\(cot^{2}x = x^{−2} = 0\). Por lo tanto, si\(x\) es una raíz de\(\tan x − x\), es una raíz de\(cot^{2}x = x^{−2}\). La expansión Taylor de\(cot^{2}x = x^{−2}\) es
\[-\frac{2}{3}(1 - \frac{1}{10}x^{2} - \frac{1}{63}x^{4} - ...). \label{6.45} \]
Debido a que el coeficiente de\(x^{2}\) es −1/10, la suma tangente-raíz\(S\) para\(\cot x = x^{−2}\) y por lo tanto\(\tan x = x\) debería ser 1/10. Como encontramos experimental y analíticamente para\(\tan x = x\), la conclusión es correcta. No obstante, ¿qué tiene de malo el razonamiento?
Problema 6.32 Cuartos poderes de los recíprocos
La serie Taylor para\(\sin x − x \cos x\) continúa
\[\frac{x^{3}}{3}(1 - \frac{x^{2}}{10} + \frac{x^{4}}{280} - ...). \label{6.46} \]
Por lo tanto encontrar\(\sum x_{n}^{−4}\) para las raíces positivas de\(\tan x = x\). Comprueba numéricamente que tu resultado sea plausible.
Problema 6.33 Otras ecuaciones fuente para las raíces
Encontrar\(\sum x_{n}^{−2}\), donde\(x_{n}\) están las raíces positivas de\(\cos x\).


