1.2.1: Sumando números enteros y aplicaciones
- Page ID
- 111157
- Sumar números enteros sin reagruparse.
- Sumar números enteros con reagrupamiento.
- Encuentra el perímetro de un polígono.
- Resolver problemas de aplicación usando la adición.
Introducción
La adición se utiliza para encontrar el número total de dos o más cantidades. El total se llama la suma, o el número que resulta de la suma. Utiliza además para encontrar la distancia total que recorres si la primera distancia es de 1,240 millas y la segunda distancia es de 530 millas. A los dos números a sumar, 1,240 y 530, se les llama las adiciones. La distancia total, 1,770 millas, es la suma.
Sumando números enteros sin reagrupar
Agregar números con más de un dígito requiere una comprensión del valor posicionar. El valor posicional de un dígito es el valor basado en su posición dentro del número. En el número 492, el 4 está en el lugar de los cientos, el 9 está en el lugar de las decenas, y el 2 está en el lugar de unos. Puede usar una línea numérica para agregar. En el siguiente ejemplo, las líneas azules representan las dos cantidades, 15 y 4, que se están sumando juntas. La línea roja representa la cantidad resultante.
15 + 4 =?
Solución

En la recta numérica, el segmento de línea azul se extiende a lo largo de 15 unidades, representando el número 15. El segundo segmento azul muestra que si agrega 4 unidades más, el número resultante es 19.
15 + 4 = 19
Se puede resolver el mismo problema sin una línea numérica, agregando verticalmente. Al sumar números con más de 1 dígito, es importante alinear sus números por valor posicionar, como en el siguiente ejemplo. Debe agregar unos a unos, decenas a decenas, cientos a cientos, y así sucesivamente.
15 + 4 =?
Solución
| \ (\\ begin {array} {r} 15\\ +\ quad 4\\ \ hline \ end {array}\) |
Debido a que 5 y 4 tienen el mismo valor posicionar, asegúrese de que estén alineados cuando agregue. |
| \ (\\ begin {array} {r} 15\\ +\ quad 4\\ \ hline 9 \ end {array}\) |
Primero, agrega los dígitos unos (los números a la derecha). El resultado va en el lugar de unos para la respuesta. |
| \ (\\ begin {array} {r} 15\\ +\ quad 4\\ \ hline 19 \ end {array}\) |
Después, agregue los dígitos de las decenas y ponga el resultado en el lugar de las decenas de la respuesta. En este caso, no hay dígito de decenas en el segundo número, por lo que el resultado es el mismo que el dígito de decenas del primer número (1). |
15 + 4 = 19
Esta estrategia de alinear los números es efectiva para sumar una serie de números también.
1 + 2 + 3 + 2 =?
Solución
\ (\\ begin {array} {r}
1\\ 2\\
3\
+2\
\ hline 8
\ end {array}\)
1 + 2 + 3 + 2 = 8
Sumando números enteros con reagrupamiento
Al sumar números enteros, una posición de valor posicional puede tener solo un dígito en ella. Si la suma de dígitos en una posición de valor posicionar es superior a 10, debe reagrupar el número de decenas a la siguiente posición de valor posicionar mayor.
Al agregar, asegúrese de alinear los dígitos de acuerdo a sus valores posicionales, como en el siguiente ejemplo. A medida que se reagrupe, coloque el dígito reagrupado por encima del dígito apropiado en la siguiente posición de valor positorio más alto y agréguelo a los números debajo de él
45 + 15 =?
Solución
| \ (\\ begin {array} {r} \ color {azul} 1\\\\ 45\ +15\\ \ hline\ color {azul} 0 \ end {array}\) |
Agrega los. Reagruparse según sea necesario. La suma de 5 y 5 es 10. Esto es 1 diez y 0 unos. Escribe el número de unos (0) en el lugar unos y el 1 diez en el lugar de las decenas por encima del 4. |
| \ (\\ begin {array} {l} &\ color {azul} 1\\ &45\\ +&15\\ \ hline & {\ color {azul} 6} 0 \ end {array}\) |
Sumar las decenas, 1 + 4 + 1 son 6 decenas. La suma final es de 60. |
45 + 15 = 60
Debe agregar dígitos en el primer lugar, los dígitos en las decenas colocan a continuación, y así sucesivamente. Ir de derecha a izquierda.
4,576 + 698 =?
Solución
| \ (\\ begin {array} {r} 4.576\\ +\ quad 698\\ \ hline \ end {array}\) |
Primero, escribe el problema con un anexo encima del otro. ¡Asegúrate de alinear los valores positoriales! |
| \ (\\ begin {array} {r} \ color {azul} 1\\\\ 4.576\\ +\ quad 698\\ \ hline\ color {azul} 4 \ end {array}\) |
Sumar los números, 6 y 8, en el lugar unos. Dado que la suma es 14, escriba el valor de unos (4) en el lugar de la respuesta. Escribe el 1 diez en el lugar de las decenas por encima del 7. |
| \ (\\ begin {array} {r} {\ color {azul} 1} 1\\\\ 4.576\\ +\ quad 698\\ \ hline {\ color {azul} 7} 4 \ end {array}\) |
Suma los números en el lugar de las decenas. Dado que la suma es de 17 decenas, reagrupa 17 decenas como cien, 7 en las decenas colocan en la respuesta y escribe el centenar en el centenar lugar por encima del 5. |
| \ (\\ begin {array} {r} {\ color {azul} 1}\\ 11\\\\ 4.576\\ +\ quad 698\\ \ hline {\ color {azul} 2} 74 \ end {array}\) |
Sumar los números en el lugar de los cientos, incluyendo el 1. Nuevamente, la suma es de más de un dígito. Renombrar 12 cientos como 2 cientos y 1 mil. Escribe el 2 en el lugar de cientos y el 1 arriba el 4 en el lugar de miles. |
| \ (\\ begin {array} {r} 1\\ 11\\\\ 4.576\\ +\ quad 698\ \ hline {\ color {azul} 5} ,274 \ end {array}\) |
Sumar los números en el lugar de miles, incluyendo el 1. La suma final es de 5,274. |
4,576 + 698 = 5,274
Adición de números mediante el método de sumas parciales
Otra forma de sumar es el método de sumas parciales. En el siguiente ejemplo, la suma de 23 + 46 se encuentra utilizando el método de sumas parciales. En este método, se suman todos los números con el mismo valor positorio y se registran sus valores (no sólo un solo dígito). Una vez que hayas hecho esto por cada valor posicional, suma sus sumas juntas.
23 + 46 =?
Solución
| Paso 1: Añadir Decenas | |
| \ (\\ begin {array} {r} 23&\ color {azul} 20\\ 46&\ color {azul} +40\\ \ hline &\ color {azul} 60 \ end {array}\) |
Comencemos sumando los valores en la posición de las decenas, la 2 y la 4. Los valores se escriben como 20 y 40. |
| Paso 2: Agregar unos | |
| \ (\\ begin {array} {r} 23&\ color {azul} 3\\ 46&\ color {azul} +6\\ \ hline &\ color {azul} 9 \ end {array}\) |
Sumar los valores en el lugar unos, los 3 y 6. |
| Paso 3: Agregar Partes | |
| \ (\\ begin {array} {r} \ color {azul} 60\ \ color {azul} +\ quad 9\ \ hline\ color {azul} 69 \ end {array}\) |
Por último, sumar las dos sumas, 60 y 9, juntas. |
23 + 46 = 69
El siguiente ejemplo agrega una serie de tres números. Observe que cientos es el mayor valor positorio ahora, por lo que cientos se agregan antes que las decenas. (Puedes agregar en cualquier orden que prefieras.) También observe que en el Paso 3, el valor en la columna ones para 350 es cero, pero aún así lo agrega para asegurarse de que todo esté contabilizado.
225 + 169 + 350 =?
Solución
| Paso 1: Agregar Cientos | |
| \ (\\ begin {array} {r} {\ color {azul} 2} 25 &\ color {azul} 200\\ {\ color {azul} 1} 69 &\ color {azul} 100\\ {\ color {azul} 3} 50 & {\ color {azul} + 300}\\ \ hline &\ color {azul} 600 \ end {array}\) |
Suma primero los valores representados por los dígitos 2, 1 y 3 en los cientos. Esto da una suma de 600. |
| Paso 2: Agregar Decenas | |
| \ (\\ begin {array} {r} 2 {\ color {azul} 2} 5 &\ color {azul} 20\\ 1 {\ color {azul} 6} 9 &\ color {azul} 60\\ 3 {\ color {azul} 5} 0&\ color {azul} +50\ \ hline &\ color {azul} 130 \ end {array}\) |
A continuación, agregue los valores de los dígitos en el lugar de las decenas, el 2, 6 y 9. La suma es de 130. |
| Paso 3: Agregar unos | |
|
\ (\\ begin {matriz} {r} 22\ color {azul} 5 &\ color {azul} 5\\ |
Suma los valores de los dígitos en el lugar unos, el 5, 9 y 0. La suma es 14. |
| Paso 4: Agregar Partes | |
| \ (\\ begin {array} {r} \ color {azul} 600\ \ color {azul} 130\ \ color {azul} +\ quad 14\ \ hline\ color {azul} 744 \ end {array}\) |
En este punto, se tiene una suma por cada valor posicional. Sumar estas tres sumas, lo que da un valor final de 744. |
225 + 169 + 350 = 744
Una empresa local construyó un parque infantil en un parque. A la compañía le tomó 124 horas planificar el patio de recreo, 243 horas para preparar el sitio, y 575 horas para construir el área de juegos. Encuentra el número total de horas que la empresa gastó en el proyecto.
- 937 horas
- 812 horas
- 742 horas
- 942 horas
- Contestar
-
- Incorrecto. Probablemente no agregaste los correctamente. La respuesta correcta es de 942 horas.
- Incorrecto. Probablemente no agregaste las decenas correctamente. La respuesta correcta es de 942 horas.
- Incorrecto. Probablemente no agregaste los cientos correctamente. La respuesta correcta es de 942 horas.
- Correcto. Llevaste a cabo el proceso de sumas parciales de manera efectiva. Las partes deben ser de 800 + 130 + 12.
Al agregar números de varios dígitos, use el método de sumas parciales o cualquier método que funcione mejor para usted.
Encontrar el perímetro de un polígono
Un polígono es una figura cerrada de muchos lados con lados que son segmentos de línea recta. Los triángulos, rectángulos y pentágonos (figuras de cinco lados) son polígonos, pero un círculo o semicírculo no lo es. El perímetro de un polígono es la distancia alrededor del polígono. Para encontrar el perímetro de un polígono, agregue las longitudes de sus lados, como en el siguiente ejemplo.
Un lado de un cuadrado tiene una longitud de 5cm. Encuentra el perímetro.
Solución
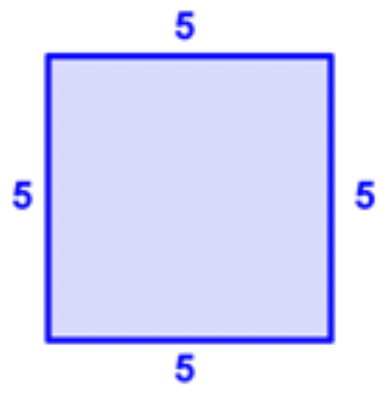 |
Dibuja el polígono y etiqueta las longitudes de los lados. Dado que las longitudes laterales de un cuadrado son iguales, cada lado es de 5cm. |
| \ (\\ begin {array} {r} 5\\ 5\\ 5\ +\ quad 5\\ \ hline 20 \ end {array}\) |
Agrega las longitudes de cada lado, 5 + 5 + 5 + 5. |
El perímetro es de 20cm.
La parte clave para completar un problema de polígono es identificar correctamente las longitudes de los lados. Una vez que conoces las longitudes laterales, las agregas como lo harías en cualquier otro problema de adición.
Una empresa planea construir un edificio. A continuación se muestra un diagrama que ilustra la forma del plano de planta del edificio. La longitud de cada lado se da en el diagrama. Las medidas para cada lado están en pies. Encuentra el perímetro del edificio.
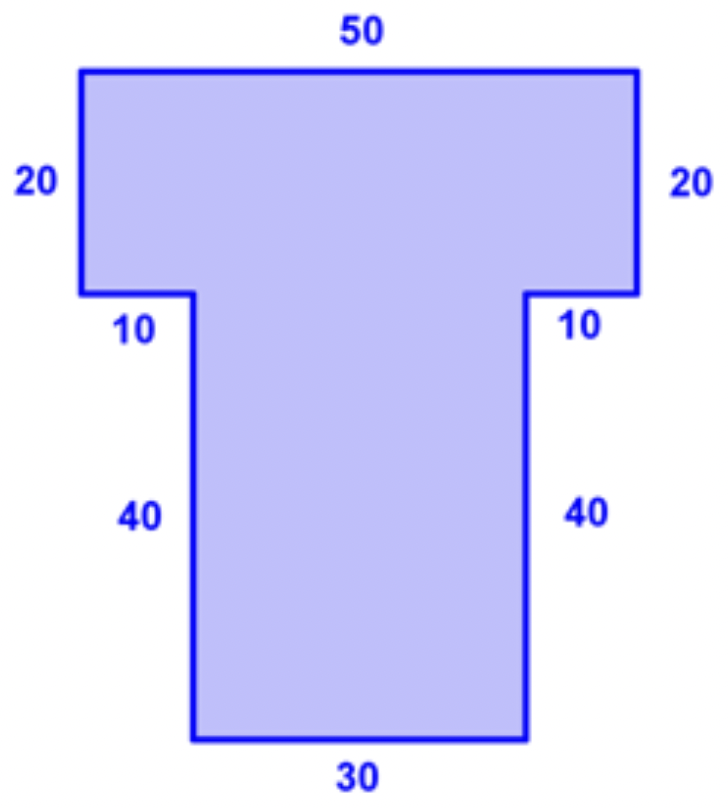
Solución
| \ (\\ begin {array} {r} 50\\ 20\\ 20\\ 10\\ 10\\ 40\\ 40\\ +30\ \ hline 220 \ end {array}\) |
Agregue las longitudes de cada lado, asegurándose de alinear todos los números de acuerdo con el valor posicionar. |
El perímetro es de 220 pies.
Encuentra el perímetro del trapecio en pies.
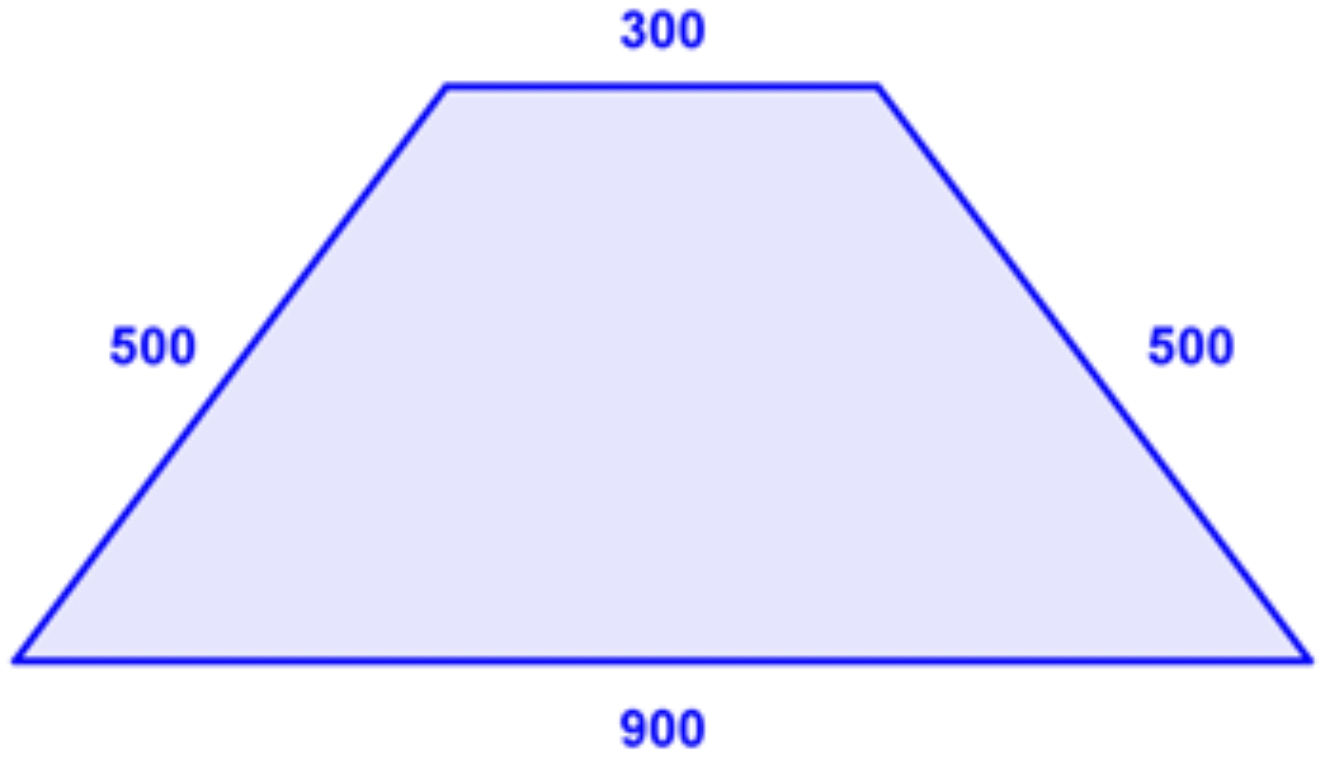
- 2,200 pies
- 1,200 pies
- 200 pies
- 3,200 pies
- Contestar
-
- Correcto. Agregaste las longitudes de los lados con éxito.
- Incorrecto. Probablemente no agregaste los dos lados diagonales del trapecio. La respuesta correcta es de 2,200 pies.
- Incorrecto. Probablemente restaste la longitud total de los dos lados, 1,000 pies, de la longitud total de la parte superior e inferior, 1,200. La respuesta correcta es de 2,200 pies.
- Incorrecto. Es posible que hayas agregado algunos de los lados más de una vez. La respuesta correcta es de 2,200 pies.
Solución de problemas de aplicación
La adición es útil para muchos tipos de problemas. Cuando veas un problema escrito en palabras, busca palabras clave que te permitan saber que necesitas agregar números.
Una mujer que prepara un mercado al aire libre está montando un stand con 321 papayas, 45 melocotones y 213 mangos. ¿Cuántos trozos de fruta en total tiene la mujer en su stand?
Solución
| \ (\\ begin {array} {r} 321\\ 45\ +213\\ \ hline \ end {array}\) |
Las palabras “cuántos... en total” sugieren que es necesario agregar los números de los diferentes tipos de frutas. Usa cualquier método que te guste para sumar los números. A continuación, se utiliza el método de sumas parciales. |
| Paso 1: Agregar Cientos | |
| \ (\\ begin {array} {r} {\ color {azul} 3} 21 &\ color {azul} 300\\ {\ color {azul} 0} 45&\ color {azul} 0\\ {\ color {azul} 2} 13 &\ color {azul} +200\\ \ hline &\ color {azul} 500 \ end {array}\) |
Sumar los números representados por los dígitos en los cientos lugar primero, los 3, 0 y 2. Esto da una suma de 500. |
| Paso 2: Agregar Decenas | |
| \ (\\ begin {array} {r} 3 {\ color {azul} 2} 1 &\ color {azul} 20\\ 0 {\ color {azul} 4} 5 &\ color {azul} 40\\ 2 {\ color {azul} 1} 3 &\ color {azul} + 10\\ \ hline &\ color {azul} 70 \ end { matriz}\) |
A continuación, agregue los números representados por los dígitos del lugar de las decenas, el 2, 4 y 1. La suma es de 70. |
| Paso 3: Agregar unos | |
| \ (\\ begin {array} {r} 32\ color {azul} 1 &\ color {azul} 1\\ 04\ color {azul} 5 &\ color {azul} 5\\ 21\ color {azul} 3 &+\ color {azul} 3\ \ hline &\ color {azul} 9 \ end {array}\) |
Suma los números de los unos, el 1, 5 y 3. |
| Paso 4: Agregar Partes | |
| \ (\\ begin {array} {r} \ color {azul} 500\ \ color {azul} 70\ \ color {azul} +\ quad 9\ \ hline\ color {azul} 579 \ final {array}\) |
Sumar las tres sumas anteriores. La suma final es 579. |
La mujer tiene 579 piezas de fruta en su estrado.
Lynn tiene 23 CDs de rock, 14 CDs de música clásica, 8 CD country y western, y 6 CD de banda sonora de películas. ¿Cuántos CDs tiene en total?
Solución
| \ (\\ begin {array} {r} 23\\ 14\\ 8\\ +6\ \ hline \ end {array}\) |
Las palabras “cuántos... en todo” sugieren que la adición es la manera de resolver este problema. Para saber cuántos CDs tiene Lynn, es necesario agregar el número de CDs que tiene para cada estilo de música. |
| \ (\\ begin {array} {r} 2\\\\ 23\\ 14\\ 8\\ +\ quad 6\\ \ hline 51 \ end {array}\) |
Usa cualquier método que prefieras para encontrar la suma de los números. |
Lynn tiene 51 CDs.
Las siguientes frases también aparecen en situaciones problemáticas que requieren adición.
| Frase | Ejemplo de problema |
| Agregar a | Jonah estaba planeando un viaje de Boston a la ciudad de Nueva York. La distancia es de 218 millas. Su hermana quería que la visitara en Springfield, Massachusetts, en su camino. Jonás sabía que esto agregaría 17 millas a su viaje. ¿Cuánto dura su viaje si visita a su hermana? |
| Plus | Carrie rentó un DVD y lo devolvió un día tarde. La tienda cobró $5 por un alquiler de dos días, más un cargo por retraso de $3. ¿Cuánto pagó Carrie por el alquiler? |
| Incrementado por | Una estadística que es importante para los futbolistas que se encuentran en posiciones ofensivas es apresurada. Después de cuatro juegos, un jugador había corrido 736 yardas. Después de dos juegos más, el número de yardas apresuradas por este jugador aumentó en 352 yardas. ¿Cuántas yardas había corrido después de los seis juegos? |
| Más de | Lavonda publicó 38 fotos en su perfil de redes sociales. Chris le publicó 27 fotos más a las suyas que Lavonda. ¿Cuántas fotos publicó Chris? |
Lena estaba planeando un viaje desde su casa en Amherst al Museo de Ciencias de Boston. El viaje es de 91 millas. Ella tuvo que tomar un desvío en el camino, lo que sumó 13 millas a su viaje. ¿Cuál es la distancia total que recorrió?
Solución
La palabra “agregado” sugiere que la adición es la manera de resolver este problema.
Para encontrar la distancia total, es necesario sumar las dos distancias.
\ (\\ begin {array} {r}
91\\
+\ quad 13\\
\ hline 104
\ end {array}\)
La distancia total es de 104 millas.
Puede ayudar a buscar palabras en un problema que implique qué operación usar. Ve si puedes encontrar la (s) palabra (s) clave (s) en el siguiente problema que te brinden pistas sobre cómo resolverlo.
Una ciudad fue golpeada por un brote de una nueva cepa de gripe en diciembre. Para evitar otro brote, 3 mil 462 personas fueron vacunadas contra la nueva cepa en enero. En febrero se vacunaron mil 298 personas adicionales. ¿Cuántas personas en total recibieron vacunas en estos dos meses?
- 2,164
- 4,760
- 4,660
- 4,750
- Contestar
-
- Incorrecto. Probablemente restaste en lugar de sumar. La respuesta correcta es 4,760.
- Correcto. Reconoció esto como un problema de adición y llevó a cabo con éxito su proceso de adición.
- Incorrecto. Probablemente no se reagruparon al lugar de los cientos, o agregaron los cientos de lugares incorrectamente. La respuesta correcta es 4,760.
- Incorrecto. Probablemente no se reagrupó al lugar de las decenas, o agregó el lugar de las decenas incorrectamente. La respuesta correcta es 4,760.
Dibujar un diagrama para resolver problemas es muy útil en campos como la ingeniería, el deporte y la arquitectura.
Un entrenador les dice a sus atletas que corran una vuelta alrededor de un campo de fútbol. El largo del campo de futbol es de 100 yardas, mientras que el ancho del campo es de 60 yardas. Encuentra la distancia total que habrá corrido cada atleta después de completar una vuelta alrededor del perímetro del campo.
Solución
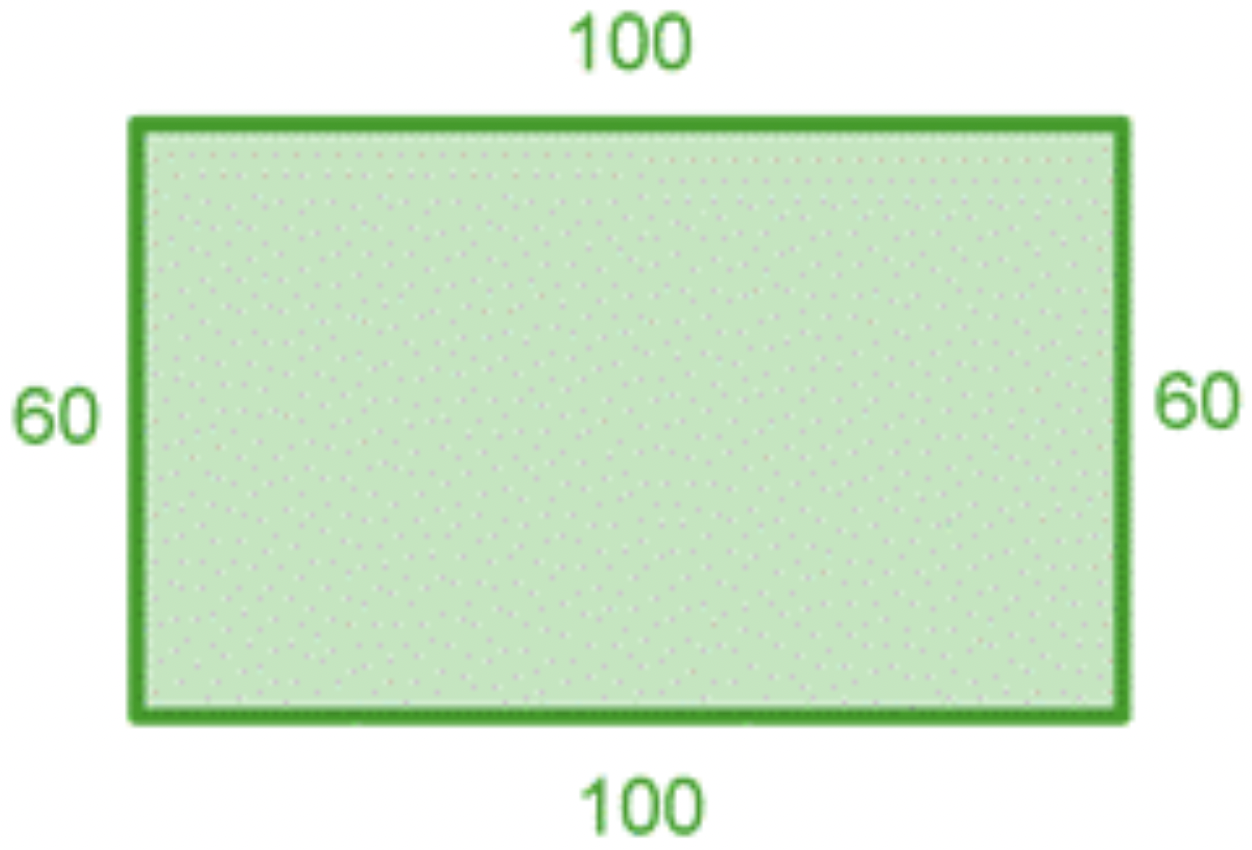 |
Las palabras “distancia total” y “perímetro” te dicen que agregues. Dibuja el campo de futbol y etiqueta los diversos lados para que puedas ver los números con los que estás trabajando para encontrar el perímetro. |
| \ (\\ begin {array} {r} \ color {azul} 1\\\\\\ 100\\ 100\\ 60\ +\ quad 60\ \ hline 20 \ end {array}\) |
Hay un cero en el lugar unos, y la suma de 6 y 6 en el lugar de las decenas es de 12 decenas. Coloca 2 decenas en el lugar de decenas en la respuesta, y reagrupa 10 decenas como cien. |
| \ (\\ begin {array} {r} \ color {azul} 1\\\\\\ 100\\ 100\\ 60\ +\ quad 60\\ hline { \\ hline {\ color {azul} 3} 20 \ end {array}\) |
Al sumar el cien a los otros dígitos en el lugar de los cientos, terminas con un 3 en el lugar de los cientos de la respuesta. |
Cada atleta habrá corrido 320 yardas.
Resumen
Puede agregar números con más de un dígito usando cualquier método, incluido el método de sumas parciales. A veces, al agregar, es posible que deba reagruparse a la siguiente posición de mayor valor posicionar. El reagrupamiento implica agrupar unos en grupos de decenas, agrupar decenas en grupos de cientos, y así sucesivamente. El perímetro de un polígono se encuentra sumando las longitudes de cada uno de sus lados.


