1.2.2: Restar números enteros y aplicaciones
- Page ID
- 111148
- Restar números enteros sin reagruparse.
- Restar números enteros con reagrupamiento.
- Resolver problemas de aplicación mediante sustracción.
Introducción
Restar implica encontrar la diferencia entre dos o más números. Es un método que se puede utilizar para una variedad de aplicaciones, como equilibrar una chequera, planificar un horario, cocinar o viajar. Supongamos que un funcionario del gobierno está fuera de Estados Unidos por negocios durante 142 días al año, incluido el tiempo de viaje. El número de días por año que se encuentra en Estados Unidos es la diferencia de 365 días y 142 días. La resta es una forma de calcular el número de días que estaría en Estados Unidos durante el año.
Al restar números, es importante alinear tus números, al igual que con la suma. El minuendo es el número mayor del que se resta el número menor. El sustraendo es el número que se resta del minuendo. Una buena manera de mantener el minuendo y restando recto es que dado que restar tiene “resta” en su inicio, va junto al signo de resta y es el número que se resta. La diferencia es la cantidad que resulta de restar el sustraendo del minuendo. En 86 - 52 = 34, 86 es el minuendo, 52 es el sustraendo, y 34 es la diferencia.
Restar números enteros
Al escribir un problema de resta, el minuendo se coloca por encima del sustraendo. Esto se puede ver en el siguiente ejemplo, donde el minuendo es 10 y el sustraendo es 7.
10 - 7 =?
Solución
\ (\\ begin {array} {r}
10\\
-\ quad 7\\
\ hline 3
\ end {array}\)
10 - 7 = 3
Cuando ambos números tengan más de un dígito, asegúrese de trabajar con un valor posicional a la vez, como en el siguiente ejemplo.
689 - 353 =?
Solución
| \ (\\ begin {array} {r} 689\\ -353\ \ hline \ end {array}\) |
Primero, configura el problema y alinea los números por valor posicionar. |
| \ (\\ begin {array} {r} 68\ color {azul} 9\\ -35\ color {azul} 3\\ \ hline\ color {azul} 6 \ end {array}\) |
Después, restar los dígitos en el lugar unos, 9 - 3. |
| \ (\\ begin {array} {r} 6 {\ color {azul} 8} 9\\ -3 {\ color {azul} 5} 3\\ \ hline {\ color {azul} 3} 6 \ end {array}\) |
A continuación, restar los dígitos en el lugar de las decenas, 8 - 5. |
| \ (\\ begin {array} {r} {\ color {azul} 6} 89\\ - {\ color {azul} 3} 53\ \ hline {\ color {azul} 3} 36 \ end {array}\) |
Por último, restar los dígitos en el lugar de los cientos, 6 - 3. |
689 - 353 = 336
Alinear números por valor posicional se vuelve especialmente importante cuando se trabaja con números más grandes que tienen más dígitos, como en el siguiente ejemplo.
9,864 - 743 =?
Solución
| \ (\\ begin {array} {r} 9864\\ -\ quad 743\ \ hline \ end {array}\) |
Primero, configura el problema y alinea los números por valor posicionar. |
| \ (\\ begin {array} {r} 986\ color {azul} 4\\ -\ quad 74\ color {azul} 3\\ \ hline\ color {azul} 1 \ end {array}\) |
Después, restar los dígitos en el lugar unos, 4 - 3. |
| \ (\\ begin {array} {r} 98 {\ color {azul} 6} 4\\ -\ quad 7 {\ color {azul} 4} 3\\ \ hline {\ color {azul} 2} 1 \ end {array}\) |
A continuación, restar los dígitos en el lugar de las decenas, 6 - 4. |
| \ (\\ begin {array} {r} 9 {\ color {azul} 8} 64\\ -\ quad {\ color {azul} 7} 43\ \ hline {\ color {azul} 1} 21 \ end {array}\) |
Ahora, resta los dígitos en el lugar de los cientos, 8 - 7. |
| \ (\\ begin {array} {r} {\ color {azul} 9} 864\\ -\ quad 743\ \ hline {\ color {azul} 9} 121 \ end {array}\) |
No hay dígito para restar en el lugar de miles, así que mantén el 9. |
9,864 - 743 = 9,121
Restar: 2,489 - 345
- 2,144
- 1,355
- 2,834
- 1,134
- Contestar
-
- Correcto. Has restado 345 con éxito de 2,489.
- Incorrecto. Probablemente no alineaste tus números correctamente por el valor positorio. La respuesta correcta es 2,144.
- Incorrecto. Probablemente agregaste cuando deberías haber restado. La respuesta correcta es 2,144.
- Incorrecto. Probablemente no restaste correctamente en las decenas y miles de lugares. La respuesta correcta es 2,144.
Restar números enteros con reagrupamiento
Es posible que tengas que reagruparte cuando restes. Cuando te reagrupas, reescribes el número para que puedas restar un dígito mayor de uno menor.
Cuando esté restando, simplemente reagrupe a la siguiente posición de valor posicional mayor en el minuendo y agregue 10 al dígito con el que esté trabajando. A medida que se reagrupa, tache el dígito reagrupado en el minuendo y coloque el nuevo dígito por encima de él. Este método se demuestra en el siguiente ejemplo.
3,225 - 476 =?
Solución
| \ (\\ begin {array} {r} 3225\\ -\ quad 476\\ \ hline \ end {array}\) |
Primero, configura el problema y alinea los dígitos por valor positorio. |
| \ (\\ begin {array} {r} {\ color {azul} 1}\\ color {rojo} 15\\ 32 {\ color {azul}\ no 2}\ color {rojo}\ no5\ -\ quad4\\ 7\\ 6\ \ hline\ color {rojo} 9 \ end {array}\) |
Ya que no se puede restar 6 de 5, reagruparse, así que 2 decenas y 5 unas se convierten en 1 diez y 15. Ahora puedes restar 6 de 15 para obtener 9. |
| \ (\\ begin {array} {r} \ color {verde oscuro} 1\ {\ color {azul} 11}\ {\ color {rojo} 15}\\ 3\ {\ color {verde oscuro}\ no 2}\\ {\ color {azul}\ no 2}\\ color {rojo}\ no 5\ -\ quad 4\\\ 7\\ 6\ \ hline {\ color {azul} 4}\\\ {\ color {rojo} 9} \ end {array}\) |
A continuación, es necesario restar 7 decenas de 1 diez. Reagrupa 2 cientos como cien, 10 decenas y suma las 10 decenas a 1 diez para obtener 11 decenas. Ahora puedes restar 7 de 11 para obtener 4. |
| \ (\\ begin {array} {r} \ color {verde} 2\\ color {verde oscuro} 11\\ color {azul} 11\\ color {rojo} 15\ \ color {verde}\ no 3\\ color {verde oscuro}\ no 2\\ color {azul}\ no 2\\ color {rojo}\ no 5\ -\ quad 4\\\ 7\\ 6\ \ hline\ color {verde oscuro} 7\\\\ color {azul} 4\\\ color {rojo} 9 \ end {array}\) |
Para restar los dígitos en el lugar de los cientos, reagrupa 3 miles como 2 miles, 10 cientos y sumar los 10 cientos al cien que ya está en el lugar de los cientos. Ahora, resta 4 de 11 para obtener 7. |
| \ (\\ begin {array} {r} \ color {verde} 2\\ color {verde oscuro} 11\\ color {azul} 11\\ color {rojo} 15 \\ color {verde}\ no 3\ color {verde oscuro}\ no 2\\ color {azul}\ no2\\ color {rojo}\ no 5\ -\ quad 4\\\ 7\\ 6\ \ hline\ color {verde} 2\\\\ color {verde oscuro} 7\\\\ color {azul} 4\\\\ color {rojo} 9 \ end {array}\) |
Como no hay dígito en el lugar de miles del sustraendo, baje el 2 en el lugar de miles en la respuesta. |
3,225 - 476 = 2,749
Restar: 1,610 - 880
- 1,522
- 2,490
- 730
- 620
- Contestar
-
- Incorrecto. Probablemente no alineaste los números por valor posicionar cuando estabas restando. La respuesta correcta es 730.
- Incorrecto. Probablemente agregaste los números en lugar de restar. La respuesta correcta es 730.
- Correcto. Has restado con éxito 880 de 1,610.
- Incorrecto. Probablemente no se reagruparon correctamente. La respuesta correcta es 730.
Comprobando su trabajo
Se puede verificar la resta sumando la diferencia y el sustraendo. La suma debe ser la misma que el minuendo.
Verifique para asegurarse de que 7 restado de 12 sea igual a 5.
Solución
| 12 - 7 = 5 | Escribe la ecuación original. El minuendo es 12, el sustraendo es 7 y la diferencia es 5. |
| \ (\\ begin {array} {r} 5\\ +\ quad 7\\ \ hline 12 \ end {array}\) |
A continuación, sumar la diferencia, 5, al sustraendo, 7, lo que resulta en el número 12. Esto confirma que tu respuesta es correcta. |
La respuesta de 5 es correcta.
Revisar tu trabajo es muy importante y siempre se debe realizar cuando el tiempo lo permita.
Restar números usando la forma expandida
Un método alternativo para restar implica escribir números en forma expandida, como se muestra en los ejemplos siguientes. Si tienes 4 decenas y quieres restar 1 diez, solo puedes pensar (4 - 1) decenas y obtener 3 decenas. Veamos cómo funciona eso.
45 - 12 =?
Solución
| \ (\\ begin {array} {l} 45=40+5\\ 12=10+2 \ end {array}\) |
Escribamos los números en forma expandida para que entiendas lo que realmente significan. |
| \ (\\ begin {array} {c} 45=40+5\\ 12=10+2\ \ hline 30 \ end {array}\) |
Para las decenas, el minuendo es 40, o 4 decenas. El sustraendo es 10, o 1 diez. Desde 4 - 1 = 3, 4 decenas -1 diez = 3 decenas, o 30. |
| \ (\\ begin {array} {r} 45=40+5\\ 12=10+2\ \ hline 30+3 \ end {array}\) |
Ahora, los unos. 5 - 2 = 3. Entonces, 30 + 3 = 33. |
45 - 12 = 33
Ahora usemos este método en el siguiente ejemplo, que pide la diferencia de 467 y 284. En el lugar de las decenas de este problema, es necesario restar 8 de 6. ¿Qué puedes hacer?
467 - 284 =?
Solución
| Paso 1: Separar por valor posicionar | |
| \ (\\ begin {array} {r} 4\ texto {cientos} +6\ texto {decenas} +7\ texto {unos}\\ -2\ texto {cientos} +8\ texto {decenas} +4\ texto {unos} \ end {array}\) |
Escribe tanto el minuendo como el sustraendo en forma expandida. |
| Paso 2: Identificar diferencias imposibles | |
| 6 - 8 =\(\ [\quad]\) | Identificar diferencias que no sean números enteros. Dado que 8 es mayor que 6, no obtendrá una diferencia numérica entera. |
| Paso 3: Reagruparse | |
| \ (\\ comenzar {array} {r} 3\ texto {cientos} + 16\ texto {decenas} +7\ texto {unos}\\ -2\ texto {cientos} + 8\ texto {decenas} +4\ texto {unos}\ \ hline 1\ texto {cien} + 8\ texto {decenas} +3\ texto {unos} \ fin {matriz}\) |
Reagrupa uno de los cientos de los 4 cientos a 10 decenas y agrégalo a las 6 decenas. Ahora tienes 16 decenas. Al restar 8 decenas de 16 decenas se obtiene una diferencia de 8 decenas. |
| Paso 4: Combine las piezas | |
| \(\ 1 \text { hundred }+8 \text { tens }+3 \text { ones }=183\) | Combinar las diferencias resultantes para cada valor positorio arroja una respuesta final de 183. |
467 - 284 = 183
Una mujer propietaria de una tienda de música inicia su semana con 965 CDs. Ella vende 452 al final de la semana. ¿Cuántos CDs le quedan?
- 313
- 513
- 510
- 1,417
- Contestar
-
- Incorrecto. Probablemente cometiste un error cuando estabas restando dígitos en el lugar de los cientos. La respuesta correcta es 513.
- Correcto. Has restado 452 de 965 con éxito. En forma expandida, 513 son 5 cientos, 1 diez y 3 unos.
- Incorrecto. Probablemente cometiste un error cuando estabas restando dígitos en el lugar de unos. La respuesta correcta es 513.
- Incorrecto. Probablemente agregaste en lugar de restar. La respuesta correcta es 513.
45 - 17 =?
Solución
| \ (\\ begin {array} {l} 45=40+5\\ 17=10+7 \ end {array}\) |
Cuando intentas restar 17 de 45, primero tratarías de restar 7 de 5. Pero 5 es menos de 7. Escribamos los números en forma expandida para que veas lo que realmente significan. |
| \ (\\ begin {array} {l} 45=30+15\\ 17=10+7\ \ hline \ end {array}\) |
Ahora, reagrupa 4 decenas como 3 decenas y 10 unas. Suma los 10 a 5 unos para obtener 15 unos, que es mayor a 7 unos, para que puedas restar. |
| \ (\\ begin {array} {r} 45=30&+&15\\ -17=10&+&7\ \ hline 20&+&8 \ end {array}\) |
Por último, restar 7 de 15, y 10 de 30 y sumar los resultados: 20 + 8 = 28. |
45 - 17 = 28
Resolver problemas de aplicación usando sustracción
Es probable que te encuentres con problemas de resta en la vida cotidiana, y ayuda a identificar frases clave en un problema que indiquen que la resta se usa o se requiere. Las siguientes frases aparecen en situaciones problemáticas que requieren sustracción.
| Frase o palabra | Ejemplo de problema |
| Menos de |
El costo de la gasolina es de 42 centavos por galón menos de lo que era el mes pasado. El costo del mes pasado fue de 280 centavos por galón. ¿Cuánto cuesta el gas este mes? |
| Take away | Howard hizo 84 cupcakes para un picnic en el vecindario. La gente se llevó 67 magdalenas. ¿Cuántos le quedan a Howard? |
| Disminuido por | La temperatura era\(\ 84^{\circ}\) Fahrenheit a primera hora de la tarde. Disminuyó\(\ 15^{\circ}\) durante la noche. ¿Cuál era la temperatura de la mañana? |
| Restado de | Jeannie trabaja en una tienda especializada a comisión. Cuando vende algo para\(\ \$ 75\), resta\(\ \$ 15\) del\(\ \$ 75\) y da el resto a la tienda. ¿Cuánto de la venta va a la tienda? |
| La diferencia | ¿Cuál es la diferencia entre la renta de este año\(\ \$ 1,530\) y la renta del año pasado\(\ \$ 1,450\)? |
| Menos de | El número de pasteles vendidos en la venta de pasteles de este año fue 15 menos que el número vendido en el mismo evento del año pasado. El año pasado se vendieron 32 tartas. ¿Cuántas tartas se vendieron este año? |
Al traducir una frase como “5 menos de 39" en una expresión matemática, el orden en que aparecen los números es crítico. Redacción 5 - 39 no sería la traducción correcta. La forma correcta de escribir la expresión es 39 - 5. Esto da como resultado el número 34, que es 5 menos que 39. El siguiente cuadro muestra cómo las frases con las palabras clave anteriores se pueden escribir como expresiones matemáticas.
| Frase | Expresión |
| tres restados de seis | 6 - 3 |
| la diferencia de diez y ocho | 10 - 8 |
| Nueve menos de 40 | 40 - 9 |
| Treinta y nueve disminuyeron en catorce | 39 - 14 |
| Ochenta y cinco para llevar doce | 85 - 12 |
| Cuatro menos de ciento ocho | 108 - 4 |
Cada año, John está fuera de los Estados Unidos por negocios durante 142 días, incluido el tiempo de viaje. El número de días por año que se encuentra en Estados Unidos es la diferencia de 365 días y 142 días. ¿Cuántos días del año tiene John en Estados Unidos?
Solución
| \ (\\ begin {array} {r} 365\\ -142\ \ hline \ end {array}\) |
Las palabras “la diferencia de” sugieren que es necesario restar para responder al problema. Primero, escriba el problema con base en la información dada y alinee los números por valor posicional, 365 - 142. |
| \ (\\ begin {array} {r} 36\ color {azul} 5\\ -14\ color {azul} 2\\ \ hline\ color {azul} 3 \ end {array}\) |
Después, restar números en el lugar unos, 5 - 2. |
| \ (\\ begin {array} {r} 3 {\ color {azul} 6} 5\\ -1 {\ color {azul} 4} 2\\ \ hline {\ color {azul} 2} 3 \ end {array}\) |
Restar números en el lugar de las decenas, 6-4. |
| \ (\\ begin {array} {r} {\ color {azul} 3} 65\\ - {\ color {azul} 1} 42\\ \ hline {\ color {azul} 2} 23 \ end {array}\) |
Por último, restar números en el lugar de los cientos, 3-1. |
John está en Estados Unidos durante 223 días durante el año.
Para asegurarse de que se le pagara el mes en su seguro de auto, Dave tuvo que pagar la diferencia del monto en su factura mensual, que era de 289 dólares, y lo que había pagado a principios de este mes, que era de 132 dólares. Escribe la diferencia de $289 y $132 como expresión matemática.
- 132-289
- 289+132
- 132+289
- 289-132
- Contestar
-
- Incorrecto. Dave había pagado 132 dólares, por lo que se le pueden quitar 132 dólares de los 289 dólares completos que adeudó por el mes. La respuesta correcta es 289-132.
- Incorrecto. Dave debe la diferencia de 132 y 289, no la suma de 289 y 132. La respuesta correcta es 289-132.
- Incorrecto. Dave debe la diferencia de 132 y 289, no la suma de 132 y 289. La respuesta correcta es 289-132.
- Correcto. La diferencia de 289 y 132 se puede escribir como 289-132.
Un pueblo africano ahora está recibiendo agua más limpia de la que solía obtener. El número de casos de cólera en el poblado ha disminuido en los últimos cinco años. Utilizando la gráfica siguiente, determinar la diferencia entre el número de casos de cólera en 2005 y el número de casos en 2010.
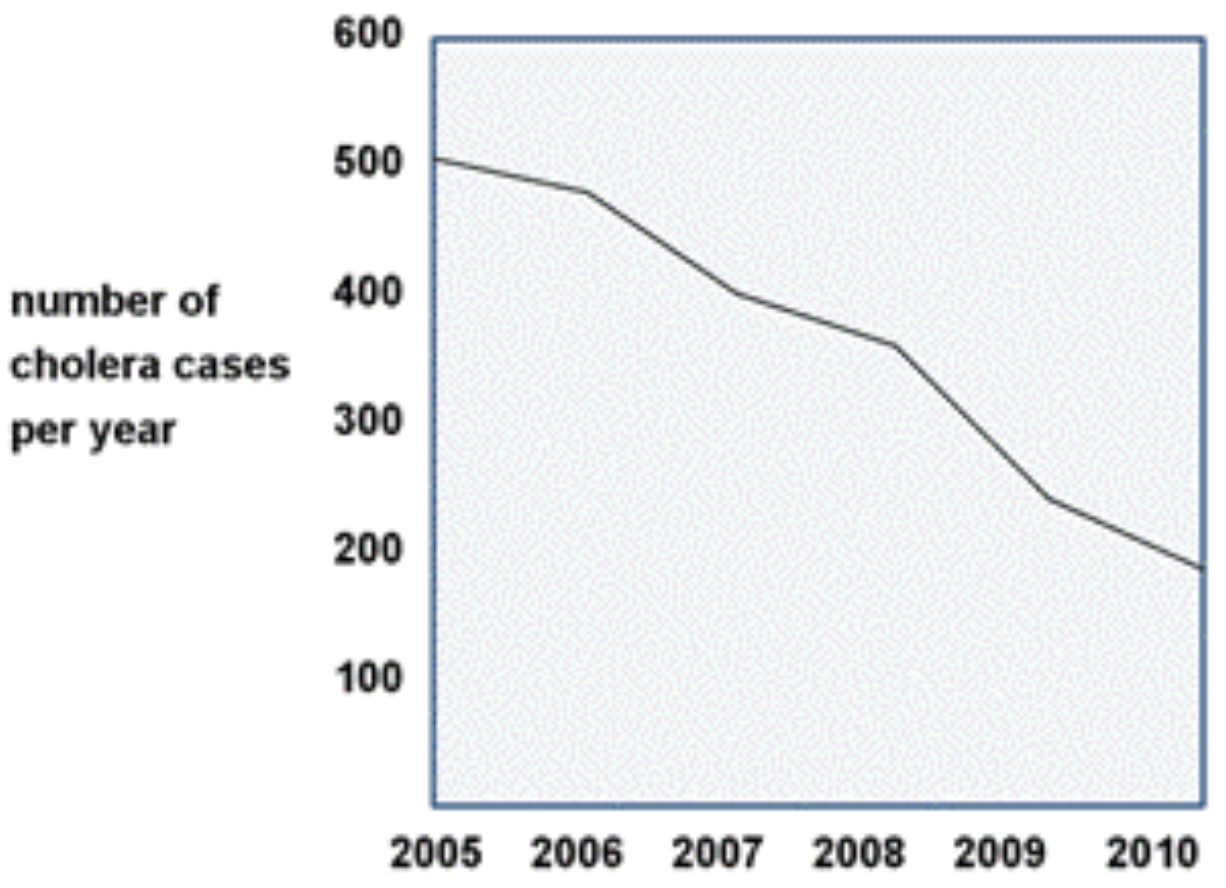
Solución
| \ (\\ begin {array} {r} 500\\ -200\ \ hline 300 \ end {array}\) |
Las palabras “la diferencia” sugieren que es necesario restar para responder al problema. En primer lugar, utilice la gráfica para encontrar el número de casos de cólera por año para los dos años: 500 en 2005 y 200 en 2010. Luego escribe el problema de la resta y alinea los números por el valor posicionar. Resta los números como lo harías normalmente. |
500-200=300 casos
Resumen
La resta se usa en innumerables áreas de la vida, como finanzas, deportes, estadísticas y viajes. Puedes identificar situaciones que requieran sustracción buscando frases clave, como diferencia y menos de. Algunos problemas de resta requieren reagruparse al siguiente valor posicional mayor, de manera que el dígito en el minuendo se vuelve mayor que el dígito correspondiente en el sustraendo. Los problemas de resta pueden resolverse sin reagruparse, si cada dígito en el minuendo es mayor que el dígito correspondiente en el sustraendo.
Además de restar usando el algoritmo estándar, la resta también se puede lograr escribiendo los números en forma expandida para que tanto el minuendo como el sustraendo se escriban como las sumas de sus valores posicionales.


