6.2.1: El Sistema Métrico
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Describir la relación general entre las unidades consuetudinarias de Estados Unidos y las unidades métricas de longitud, peso/masa y volumen.
- Defina los prefijos métricos y utilícelos para realizar conversiones básicas entre unidades métricas.
Introducción
En Estados Unidos, se utilizan tanto el sistema de medición habitual de Estados Unidos como el sistema métrico, especialmente en los campos médico, científico y técnico. En la mayoría de los demás países, el sistema métrico es el principal sistema de medición. Si viajas a otros países, verás que las señales viales indican distancias en kilómetros y la leche se vende en litros. La gente en muchos países usa palabras como “kilómetro”, “litro” y “miligramo” para medir la longitud, el volumen y el peso de diferentes objetos. Estas unidades de medida forman parte del sistema métrico.
A diferencia del sistema de medición habitual de Estados Unidos, el sistema métrico se basa en 10s. Por ejemplo, un litro es 10 veces mayor que un decilitro, y un centigramo es 10 veces mayor que un miligramo. Esta idea de “10” no está presente en el sistema habitual de Estados Unidos: ¡hay 12 pulgadas en un pie, 3 pies en una yarda y 5.280 pies en una milla!
Entonces, ¿y si tienes que averiguar cuántos miligramos hay en un decigramo? O, ¿y si quieres convertir metros a kilómetros? Entender cómo funciona el sistema métrico es un buen comienzo.
¿Qué es Metric?
El sistema métrico utiliza unidades como metro, litro y gramo para medir la longitud, el volumen de líquido y la masa, así como el sistema habitual de Estados Unidos usa pies, cuartos de galón y onzas para medirlos.
Además de la diferencia en las unidades básicas, el sistema métrico se basa en 10s, y las diferentes medidas de longitud incluyen kilómetro, metro, decímetro, centímetro y milímetro. Observe que la palabra “metro” forma parte de todas estas unidades.
El sistema métrico también aplica la idea de que las unidades dentro del sistema se hacen más grandes o más pequeñas en una potencia de 10. Esto significa que un metro es 100 veces mayor que un centímetro, y un kilogramo es 1,000 veces más pesado que un gramo. Explorarás esta idea un poco más tarde. Por ahora, observe cómo esta idea de “hacerse más grande o menor en 10” es muy diferente a la relación entre unidades en el sistema habitual de Estados Unidos, donde 3 pies equivale a 1 yarda y 16 onzas equivale a 1 libra.
Longitud, masa y volumen
En la siguiente tabla se muestran las unidades básicas del sistema métrico. Tenga en cuenta que los nombres de todas las unidades métricas siguen de estas tres unidades básicas.
| Largo | Masa | Volumen |
|---|---|---|
| unidades básicas | ||
| medidor | gramo | litro |
| otras unidades que puede ver | ||
| kilómetro | kilogramo | dekaliter |
| centímetro | centigramo | centilitro |
| milímetro | miligramo | mililitro |
En el sistema métrico, la unidad básica de longitud es el metro. Un metro es un poco más grande que un patrón, o poco más de tres pies.
La unidad métrica básica de masa es el gramo. Un clip de tamaño regular tiene una masa de aproximadamente 1 gramo.
Entre los científicos, un gramo se define como la masa de agua que llenaría un cubo de 1 centímetro. Puede notar que aquí se usa la palabra “masa” en lugar de “peso”. En los campos de las ciencias y la técnica, se hace una distinción entre peso y masa. El peso es una medida del tirón de la gravedad sobre un objeto. Por esta razón, el peso de un objeto sería diferente si se pesara en la Tierra o en la luna debido a la diferencia en las fuerzas gravitacionales. Sin embargo, la masa del objeto permanecería igual en ambos lugares porque la masa mide la cantidad de sustancia en un objeto. Siempre y cuando planees medir solo objetos en la Tierra, puedes usar masa/peso de manera bastante intercambiable, ¡pero vale la pena señalar que hay una diferencia!
Por último, la unidad métrica básica de volumen es el litro. Un litro es un poco más grande que un cuarto de galón.
 |
 |
 |
| El mango de una pala es de aproximadamente 1 metro. | Un clip pesa aproximadamente 1 gramo. | Un recipiente mediano de leche es de aproximadamente 1 litro. |
Aunque rara vez es necesario convertir entre los sistemas habituales y métricos, a veces ayuda tener una imagen mental de cuán grandes o pequeñas son algunas unidades. La siguiente tabla muestra la relación entre algunas unidades comunes en ambos sistemas.
| Mediciones comunes en sistemas habituales y métricos | |
| Largo | 1 centímetro es un poco menos de media pulgada. |
| 1.6 kilómetros es de aproximadamente 1 milla. | |
| 1 metro es aproximadamente 3 pulgadas más largo que 1 yarda. | |
| Masa | 1 kilogramo es un poco más de 2 libras. |
| 28 gramos es aproximadamente lo mismo que 1 onza. | |
| Volumen | 1 litro es un poco más de 1 cuarto de galón. |
| 4 litros es un poco más de 1 galón. |
Prefijos en el sistema métrico
El sistema métrico es un sistema base 10. Esto significa que cada unidad sucesiva es 10 veces mayor que la anterior.
Los nombres de las unidades métricas se forman añadiendo un prefijo a la unidad básica de medida. Para decir qué tan grande o pequeña es una unidad, miras el prefijo. Para saber si la unidad mide longitud, masa o volumen, miras la base.
| kilo | 1,000 veces más grande que la unidad base |
| hecto | 100 veces más grande que la unidad base |
| deka | 10 veces más grande que la unidad base |
| metro, gramo, litro | unidades base |
| deci- | 10 veces más pequeño que la unidad base |
| centi- | 100 veces más pequeño que la unidad base |
| milli- | 1,000 veces más pequeño que la unidad base |
Usando esta tabla como referencia, puede ver lo siguiente:
- Un kilogramo es 1,000 veces más grande que un gramo (entonces\ 1 \text { kilogram }=1,000 \text { grams }).
- Un centímetro es 100 veces menor que un metro (así\ 1 \text { meter }=100 \text { centimeters }).
- Un dekaliter es 10 veces más grande que un litro (entonces\ 1 \text { dekaliter }=10 \text { liters }).
Aquí hay una tabla similar que solo muestra las unidades métricas de medida para la masa, junto con su tamaño relativo a 1 gramo (la unidad base). También se han incluido las abreviaturas comunes para estas unidades métricas.
| kilogramo (kg) | \ 1,000 \text { grams } |
| hectograma (hg) | \ 100 \text { grams } |
| dekagram (dag) | \ 10 \text { grams } |
| gramo (g) | \ \text { gram } |
| decigrama (dg) | \ 0.1 \text { gram } |
| centigramo (cg) | \ 0.01 \text { gram } |
| miligramo (mg) | \ 0.001 \text { gram } |
Dado que los prefijos permanecen constantes a través del sistema métrico, podría crear gráficos similares para longitud y volumen. Los prefijos tienen los mismos significados ya sea que estén unidos a las unidades de longitud (metro), masa (gramo) o volumen (litro).
¿Cuáles de los siguientes conjuntos de tres unidades son medidas métricas de longitud?
- pulgada, pie, yarda
- kilómetro, centímetro, milímetro
- kilogramo, gramo, centigramo
- kilómetro, pie, decímetro
- Contestar
-
- Incorrecto. Aunque estas unidades miden la longitud, todas son unidades de medida del sistema habitual de Estados Unidos. La respuesta correcta es kilómetro, centímetro, milímetro.
- Correcto. Todas estas medidas son del sistema métrico. Se puede decir que son medidas de longitud porque todas contienen la palabra “metro”.
- Incorrecto. Estas medidas son del sistema métrico, pero son medidas de masa, no de longitud. La respuesta correcta es kilómetro, centímetro, milímetro.
- Incorrecto. El kilómetro y el decímetro son unidades métricas de longitud, pero el pie no lo es. La respuesta correcta es kilómetro, centímetro, milímetro.
Conversión de unidades hacia arriba y hacia abajo en la escala métrica
La conversión entre unidades métricas de medida requiere el conocimiento de los prefijos métricos y la comprensión del sistema decimal. Eso es todo.
Por ejemplo, puedes averiguar cuántos centigramos hay en un dekagrama usando la tabla anterior. Un dekagrama es mayor que un centigramo, por lo que se espera que un dekagrama sea igual a muchos centigramos.
En la tabla, cada unidad es 10 veces mayor que la que se encuentra a su derecha inmediata. Esto significa que\ 1 \text { dekagram }=10 \text { grams };\ 10 \text { grams }=100 \text { decigrams }; y\ 100 \text { decigrams }=1,000 \text { centigrams }. Entonces,\ 1 \text { dekagram }=1,000 \text { centigrams }.
¿Cuántos miligramos hay en un decigramo?
Solución
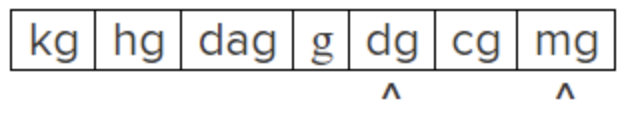 |
Identificar ubicaciones de miligramos y decigramas. Los decigramas (dg) son más grandes que los miligramos (mg), por lo que se espera que haya muchos mg en una dg. |
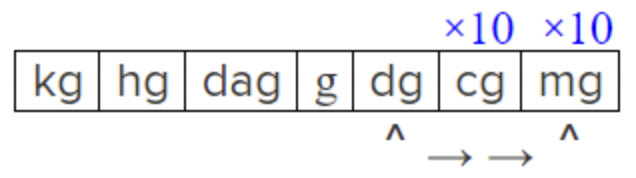 |
Dg es 10 veces mayor que un cg, y un cg es 10 veces mayor que un mg. |
| \ 1 \mathrm{dg} \cdot 10 \cdot 10=100 \mathrm{mg} |
Ya que vas de una unidad más grande a una unidad más pequeña, multiplica. Multiplicar:\ 1 \cdot 10 \cdot 10, para encontrar el número de miligramos en un decigramo. |
Hay 100 miligramos (mg) en 1 decigramo (dg).
Convierte 1 centímetro en kilómetros.
Solución
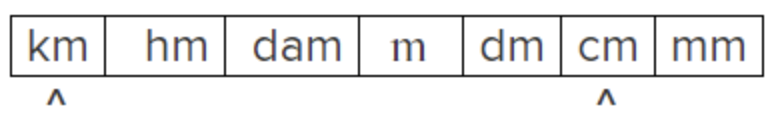 |
Identificar ubicaciones de kilómetros y centímetros. Los kilómetros (km) son mayores que centímetros (cm), por lo que se espera que haya menos de un km en un cm. |
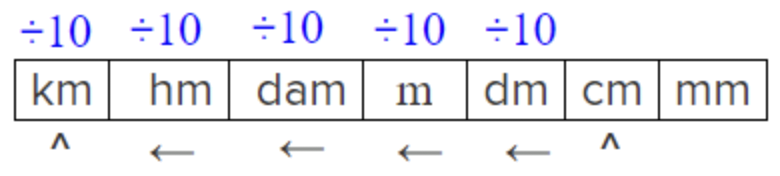 |
Cm es 10 veces menor que un dm; un dm es 10 veces menor que un m, etc. Ya que vas de una unidad más pequeña a una unidad más grande, divide. |
| \ 1 \text { centimeter } \div 10 \div 10 \div 10 \div 10 \div 10=0.00001 \text { kilometers } | Dividir:\ 1 \div 10 \div 10 \div 10 \div 10 \div 10 para encontrar el número de kilómetros en un centímetro. |
\ 1 \text { centimeter }(\mathrm{cm})=0.00001 \text { kilometers }(\mathrm{km}).
Una vez que comiences a entender el sistema métrico, puedes usar un atajo para convertir entre diferentes unidades métricas. El tamaño de las unidades métricas aumenta diez veces a medida que sube la escala métrica. El sistema decimal funciona de la misma manera: una décima es 10 veces mayor que una centésima; una centésima es 10 veces mayor que una milésima, etc. Al aplicar lo que sabes sobre decimales al sistema métrico, convertir entre unidades es tan simple como mover puntos decimales.
Aquí está el primer problema desde arriba: ¿Cuántos miligramos hay en un decigramo? Puede recrear el orden de las unidades métricas como se muestra a continuación:
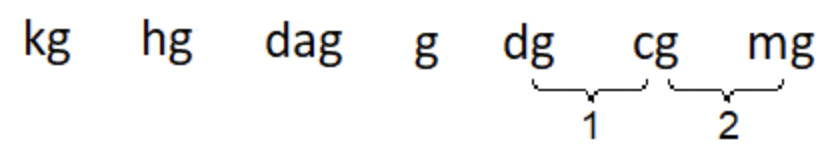
Esta pregunta te pide comenzar con 1 decigramo y convertirlo en miligramos. Como se muestra arriba, los miligramos son dos lugares a la derecha de los decigramas. Simplemente puede mover el punto decimal dos lugares a la derecha para convertir decigramas a miligramos:
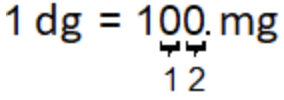
El mismo método funciona cuando estás convirtiendo de una unidad más pequeña a otra más grande, como en el problema: Convertir 1 centímetro a kilómetros.
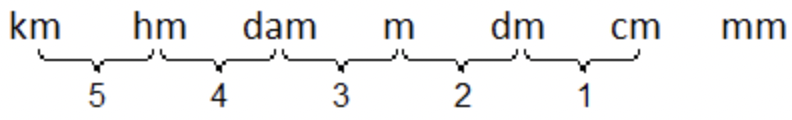
Tenga en cuenta que en lugar de moverse hacia la derecha, ahora se está moviendo hacia la izquierda, por lo que el punto decimal debe hacer lo mismo:
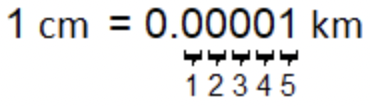
¿Cuántos mililitros hay en 1 litro?
- 0.001
- 0.1
- 100
- 1,000
- Contestar
-
- Incorrecto. Un litro es mayor que un mililitro, por lo que esperarías que haya más de un mililitro en 1 litro. La respuesta correcta es 1,000.
- Incorrecto. Un litro es mayor que un mililitro, por lo que esperarías que haya más de un mililitro en 1 litro. La respuesta correcta es 1,000.
- Incorrecto. Hay 100 mililitros en 1 decilitro. La respuesta correcta es 1,000.
- Correcto. Hay 10 mililitros en un centilitro, 10 centilitros en un decilitro y 10 decilitros en un litro. Multiplicar:\ 10 \cdot 10 \cdot 10, para encontrar el número de mililitros en un litro, 1,000.
Resumen
El sistema métrico es el sistema de medición utilizado en la mayoría de los países, y también es un sistema alternativo en Estados Unidos. El sistema métrico se basa en unir uno de una serie de prefijos, incluyendo kilo-, hecto-, deka-, deci-, centi- y milli-, con una unidad base de medida, como metro, litro o gramo. Las unidades en el sistema métrico están todas relacionadas por una potencia de 10, lo que significa que cada unidad sucesiva es 10 veces mayor que la anterior. Esto hace que convertir una medida métrica a otra sea un proceso sencillo, y a menudo es tan simple como mover un punto decimal. Siempre es importante, sin embargo, considerar la dirección de la conversión. Si está convirtiendo una unidad más pequeña en una unidad más grande, entonces el punto decimal tiene que moverse hacia la izquierda (haciendo que su número sea más pequeño); si está convirtiendo una unidad más grande en una unidad más pequeña, entonces el punto decimal tiene que moverse hacia la derecha (haciendo que su número sea más grande).


