7.2.1: Cuadriláteros

Objetivos de aprendizaje

• Identificar propiedades, incluyendo mediciones de ángulo, de cuadriláteros.

Introducción

Los cuadriláteros son un tipo especial de polígono. Al igual que con los triángulos y otros polígonos, los cuadriláteros tienen propiedades especiales y pueden clasificarse por características de sus ángulos y lados. Comprender las propiedades de diferentes cuadriláteros puede ayudarte a resolver problemas que involucran este tipo de polígono.

Definición de un cuadrilátero

Escogiendo el nombre “cuadrilátero” te ayuda a entender a qué se refiere. El prefijo “quad-” significa “cuatro”, y “lateral” se deriva de la palabra latina para “lado”. Entonces un cuadrilátero es un polígono de cuatro lados.

Al tratarse de un polígono, ya sabes que se trata de una figura bidimensional conformada por lados rectos. Un cuadrilátero también tiene cuatro ángulos formados por sus cuatro lados. A continuación se presentan algunos ejemplos de cuadriláteros. Observe que cada figura tiene cuatro lados rectos y cuatro ángulos.

Ángulos interiores de un cuadrilátero

La suma de los ángulos interiores de cualquier cuadrilátero es de 360 ^o. Considera los dos ejemplos que aparecen a continuación.

Podrías dibujar muchos cuadriláteros como estos y medir cuidadosamente los cuatro ángulos. Encontrarías que por cada cuadrilátero, la suma de los ángulos interiores siempre será de 360 ^o.

También puedes usar tus conocimientos de triángulos como una forma de entender por qué la suma de los ángulos interiores de cualquier cuadrilátero es de 360 ^o. Cualquier cuadrilátero se puede dividir en dos triángulos como se muestra en las imágenes a continuación.

En la primera imagen, los cuadriláteros se han dividido cada uno en dos triángulos. Se muestran las medidas de ángulo de un triángulo para cada uno.

Estas medidas suman 180 ^o. Ahora mira las medidas para los otros triángulos. ¡También suman 180 ^o!

Dado que la suma de los ángulos interiores de cualquier triángulo es de 180 ^o y hay dos triángulos en un cuadrilátero, la suma de los ángulos para cada cuadrilátero es de 360 ^o.

Tipos Específicos de Cuadriláteros

Empecemos por examinar el grupo de cuadriláteros que tienen dos pares de lados paralelos. Estos cuadriláteros se llaman paralelogramos Toman una variedad de formas, pero a continuación se muestra un ejemplo clásico.

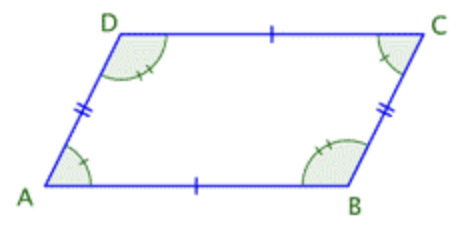
Imagina extender los pares de lados opuestos. Nunca se cruzarían porque son paralelos. Observe, también, que los ángulos opuestos de un paralelogramo son congruentes, al igual que los lados opuestos. (Recuerda que “congruente” significa “del mismo tamaño”.) El símbolo geométrico para congruente es\(\ \cong\), para que puedas escribir\(\ \angle A \cong \angle C\) y\(\ \angle B \cong \angle D\). Los lados paralelos también tienen la misma longitud:\(\ \overline{A B} \cong \overline{D C}\) y\(\ \overline{B C} \cong \overline{A D}\). Estas relaciones son ciertas para todos los paralelogramos.

Hay dos casos especiales de paralelogramos que te serán familiares desde tus primeras experiencias con formas geométricas. El primer caso especial se llama rectángulo. Por definición, un rectángulo es un paralelogramo porque sus pares de lados opuestos son paralelos. Un rectángulo también tiene la característica especial de que todos sus ángulos son ángulos rectos; sus cuatro ángulos son congruentes.

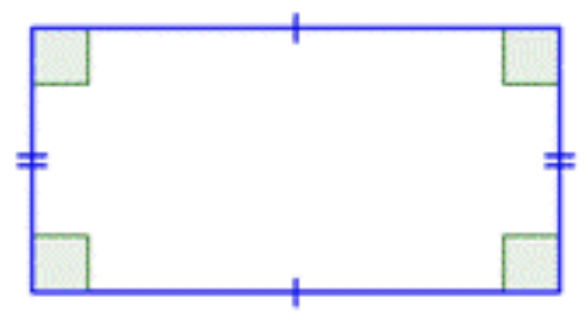
El otro caso especial de un paralelogramo es un tipo especial de rectángulo, un cuadrado. Un cuadrado es una de las formas geométricas más básicas. Se trata de un caso especial de un paralelogramo que tiene cuatro lados congruentes y cuatro ángulos rectos.

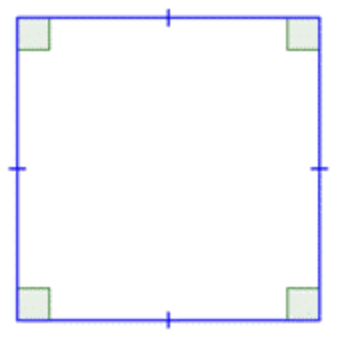
Un cuadrado también es un rectángulo porque tiene dos juegos de lados paralelos y cuatro ángulos rectos. Un cuadrado es también un paralelogramo porque sus lados opuestos son paralelos. Entonces, un cuadrado se puede clasificar en cualquiera de estas tres formas, siendo “paralelogramo” la descripción menos específica y “cuadrado”, la más descriptiva.

Otro cuadrilátero que podrías ver se llama rombo. Los cuatro lados de un rombo son congruentes. Sus propiedades incluyen que cada par de lados opuestos es paralelo, convirtiéndolo también en un paralelogramo.

En resumen, todos los cuadrados son rectángulos, pero no todos los rectángulos son cuadrados. Todos los rectángulos son paralelogramos, pero no todos los paralelogramos son rectángulos. Y todas estas formas son cuadriláteros.

El siguiente diagrama ilustra la relación entre los diferentes tipos de cuadriláteros.

Se pueden utilizar las propiedades de los paralelogramos para resolver problemas. Considera el ejemplo que sigue.

Ejemplo

Determinar las medidas de\(\ \angle M\) y\(\ \angle L\).

Solución

\(\ \angle L \text { is opposite } \angle J\) \(\ \angle M \text { is opposite } \angle K\)	Identificar ángulos opuestos.
\ (\\ begin {array} {r} \ ángulo L\ cong\ ángulo J\ \ ángulo M\ cong\ ángulo K \ final {matriz}\)	Una propiedad de los paralelogramos es que los ángulos opuestos son congruentes.
\ (\\ begin {array} {r} m\ ángulo J=60^ {\ circ},\ text {so} m\ ángulo L=60^ {\ circ}\\ m\ ángulo K=120^ {\ circ},\ text {so} m\ ángulo M=120^ {\ circ} \ end {array}\)	Utilice las medidas de ángulo dadas para determinar medidas de ángulos opuestos.

\(\ m \angle L=60^{\circ} \text { and } m \angle M=120^{\circ}\)

Trapezoides

Hay otro tipo especial de cuadrilátero. Este cuadrilátero tiene la propiedad de tener sólo un par de lados opuestos que son paralelos. Aquí hay un ejemplo de trapecio.

Observe eso\(\ \overline{X Y} \| \overline{W Z}\), y eso\(\ \overline{W X}\) y no\(\ \overline{Z Y}\) son paralelos. Se puede imaginar fácilmente que si extendieras los lados\(\ \overline{W X}\) y\(\ \overline{Z Y}\), ellos se cruzarían por encima de la figura.

Si los lados no paralelos de un trapecio son congruentes, el trapecio se llama trapecio isósceles. Al igual que el triángulo de nombre similar que tiene dos lados de igual longitud, el trapecio isósceles tiene un par de lados opuestos de igual longitud. El otro par de lados opuestos es paralelo. A continuación se muestra un ejemplo de un trapecio isósceles.

En este trapecio\(\ A B C D, \overline{B C} \| \overline{A D} \text { and } \overline{A B} \cong \overline{C D}\).

Ejercicio

¿Cuál de las siguientes afirmaciones es cierta?

1. Algunos trapecios son paralelogramos.
2. Todos los trapecios son cuadriláteros.
3. Todos los rectángulos son cuadrados.
4. Una forma no puede ser un paralelogramo y un cuadrilátero.

Contestar

1. Incorrecto. Los trapezoides tienen solo un par de lados paralelos; los paralelogramos tienen dos pares de lados paralelos. Un trapecio nunca puede ser un paralelogramo. La respuesta correcta es que todos los trapecios son cuadriláteros.
2. Correcto. Los trapezoides son polígonos de cuatro lados, por lo que todos son cuadriláteros.
3. Incorrecto. Algunos rectángulos pueden ser cuadrados, pero no todos los rectángulos tienen cuatro lados congruentes. Sin embargo, todos los cuadrados son rectángulos. La respuesta correcta es que todos los trapecios son cuadriláteros.
4. Incorrecto. Todos los paralelogramos son cuadriláteros, por lo que si es un paralelogramo, también es un cuadrilátero. La respuesta correcta es que todos los trapecios son cuadriláteros.

Se pueden utilizar las propiedades de los cuadriláteros para resolver problemas que involucran trapecios. Considera el siguiente ejemplo.

Ejemplo

Encuentra la medida de\(\ \angle Q\).

Solución

\(\ m \angle P+m \angle Q+m \angle R+m \angle S=360^{\circ}\)	La suma de las medidas de los ángulos interiores de un cuadrilátero es de 360 ^o.
\ (\\ start {array} {l} m\ ángulo R=90^ {\ circ}\\ m\ ángulo S=90^ {\ circ} \ end {array}\)	El símbolo cuadrado indica un ángulo recto.
\(\ 60^{\circ}+m \angle Q+90^{\circ}+90^{\circ}=360^{\circ}\)	Dado que se dan tres de las cuatro medidas de ángulo, puede encontrar la cuarta medición de ángulo.
\ (\\ comenzar {alineado} m\ ángulo Q+240^ {\ circ} &=360^ {\ circ}\\ m\ ángulo Q &=120^ {\ circ} \ final {alineado}\)	Ahora, para\(\ \angle Q\), calcular la medición. De la imagen, se puede ver que se trata de un ángulo obtuso, por lo que su medida debe ser mayor a 90 ^o.

\(\ m \angle Q=120^{\circ}\)

La siguiente tabla resume los tipos especiales de cuadriláteros y algunas de sus propiedades.

Nombre de Cuadrilátero	Cuadrilátero	Descripción
Paralelogramo		2 pares de lados paralelos. Los lados opuestos y los ángulos opuestos son congruentes.
Rectángulo		2 pares de lados paralelos. 4 ángulos rectos (90 ^o). Los lados opuestos son paralelos y congruentes. Todos los ángulos son congruentes.
Cuadrado		4 lados congruentes. 4 ángulos rectos (90 ^o). Los lados opuestos son paralelos. Todos los ángulos son congruentes.
Trapezoide		Sólo un par de lados opuestos es paralelo.

Resumen

Un cuadrilátero es un nombre matemático para un polígono de cuatro lados. Los paralelogramos, cuadrados, rectángulos y trapecios son ejemplos de cuadriláteros. Estos cuadriláteros ganan su distinción en función de sus propiedades, incluyendo el número de pares de lados paralelos que tienen y sus medidas de ángulo y lado.