7.2.3: Círculos
- Page ID
- 111352
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Identificar las propiedades de los círculos.
- Encuentra la circunferencia de un círculo.
- Encuentra el área de un círculo.
- Encuentra el área y perímetro de figuras geométricas compuestas.
Introducción
Los círculos son una forma común. Los ves por todas partes: ruedas en un automóvil, Frisbees pasando por el aire, discos compactos entregando datos. Todos estos son círculos.
Un círculo es una figura bidimensional al igual que polígonos y cuadriláteros. Sin embargo, los círculos se miden de manera diferente a estas otras formas. Incluso tienes que usar algunos términos diferentes para describirlos. Echemos un vistazo a esta interesante forma.
Propiedades de Circles
Un círculo representa un conjunto de puntos, todos los cuales están a la misma distancia de un punto medio fijo. Este punto fijo se llama el centro. La distancia desde el centro del círculo (punto A) hasta cualquier punto del círculo (punto B) se denomina radio. Un círculo es nombrado por el punto en su centro, por lo que este círculo se llamaría Círculo A.
Cuando se juntan dos radios (el plural del radio) para formar un segmento de línea a través del círculo, se tiene un diámetro. El diámetro de un círculo pasa por el centro del círculo y tiene sus extremos en el círculo mismo.
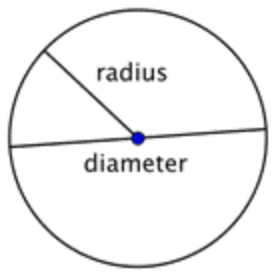
El diámetro de cualquier círculo es dos veces la longitud del radio de ese círculo. Se puede representar por la expresión\(\ 2r\), o “dos veces el radio”. Entonces, si conoces el radio de un círculo, puedes multiplicarlo por 2 para encontrar el diámetro; esto también significa que si conoces el diámetro de un círculo, puedes dividirlo por 2 para encontrar el radio.
Encuentra el diámetro del círculo.
Solución
| \ (\\ begin {array} {c} d=2 r\\ d=2 (7)\\ d=14 \ end {array}\) |
El diámetro es dos veces el radio, o\(\ 2r\). El radio de este círculo es de 7 pulgadas, por lo que el diámetro es de\(\ 2(7)=14\) pulgadas. |
El diámetro es de 14 pulgadas.
Encuentra el radio del círculo.
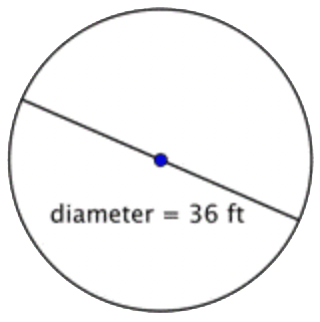
Solución
| \ (\\ begin {array} {c} r=\ frac {1} {2} d\\ r=\ frac {1} {2} (36)\\ r=18 \ end {array}\) |
El radio es la mitad del diámetro, o\(\ \frac{1}{2} d\). El diámetro de este círculo es de 36 pies, por lo que el radio es\(\ \frac{1}{2}(36)=18\) pies. |
El radio es de 18 pies.
Circunferencia
La distancia alrededor de un círculo se llama circunferencia. (Recordemos, la distancia alrededor de un polígono es el perímetro.)
Una propiedad interesante sobre los círculos es que la relación entre la circunferencia de un círculo y su diámetro es la misma para todos los círculos. No importa el tamaño del círculo, la relación entre la circunferencia y el diámetro será la misma.
A continuación se proporcionan algunas medidas reales de diferentes artículos. Las mediciones son precisas al milímetro o cuarto de pulgada más cercano (dependiendo de la unidad de medida utilizada). Observa la relación entre la circunferencia y el diámetro de cada uno. Si bien los ítems son diferentes, la proporción para cada uno es aproximadamente la misma.
| Artículo | Circunferencia (\(\ C\)) (redondeada a la centésima más cercana) | Diámetro (\(\ d\)) | Ratio\(\ \frac{C}{d}\) |
| Copa | 253 mm | 79 mm | \(\ \frac{253}{79}=3.2025 \ldots\) |
| Trimestre | 84 mm | 27 mm | \(\ \frac{84}{27}=3.1111 \ldots\) |
| Tazón | 37.25 pulgadas | 11.75 pulgadas | \(\ \frac{37.25}{11.75}=3.1702 \ldots\) |
La circunferencia y el diámetro son medidas aproximadas, ya que no existe una manera precisa de medir estas dimensiones exactamente. Si pudieras medirlas con mayor precisión, sin embargo, encontrarías que la relación se\(\ \frac{C}{d}\) movería hacia 3.14 por cada uno de los ítems dados. El nombre matemático para la relación\(\ \frac{C}{d}\) es pi, y está representado por la letra griega\(\ \pi\).
\(\ \pi\)es un decimal no terminante, no repetitivo, por lo que es imposible escribirlo por completo. Los primeros 10 dígitos de\(\ \pi\) son 3.141592653; a menudo se redondea a 3.14 o se estima como la fracción\(\ \frac{22}{7}\). Obsérvese que tanto 3.14 como\(\ \frac{22}{7}\) son aproximaciones de\(\ \pi\), y se utilizan en cálculos donde no es importante ser precisos.
Ya que sabes que la relación de circunferencia a diámetro (o\(\ \pi\)) es consistente para todos los círculos, puedes usar este número para encontrar la circunferencia de un círculo si conoces su diámetro.
\(\ \frac{C}{d}=\pi, \text { so } C=\pi d\)
\(\ \text { Also, since } d=2 r, \text { then } C=\pi d=\pi(2 r)=2 \pi r\).
Para encontrar la circunferencia (\(\ C\)) de un círculo, utilice una de las siguientes fórmulas:
Si conoce el diámetro (\(\ d\)) de un círculo:\(\ C=\pi d\)
Si conoce el radio (\(\ r\)) de un círculo:\(\ C=2 \pi r\)
Encuentra la circunferencia del círculo.
Solución
| \ (\\ comenzar {matriz} {l} C=\ pi d\\ C=\ pi\ cdot 9\\ C\ aprox 3.14\ cdot 9\\ C\ aproximadamente 28.26 \ final {array}\) |
Para calcular la circunferencia dada un diámetro de 9 pulgadas, usa la fórmula\(\ C=\pi d\). Utilice 3.14 como aproximación para\(\ \pi\). |
| Ya que estás usando una aproximación para\(\ \pi\), no puedes dar una medida exacta de la circunferencia. En su lugar, usa el símbolo\(\ \approx\) para indicar “aproximadamente igual a”. |
La circunferencia es de 9\(\ \pi\) o aproximadamente 28.26 pulgadas.
Encuentra la circunferencia de un círculo con un radio de 2.5 yardas.
Solución
| \ (\\ comenzar {matriz} {l} C=2\ pi r\\ C=2\ pi\ cdot 2.5\\ C=\ pi\ cdot 5\\ C\ aprox 3.14\ cdot 5\\ C\ aproximadamente 15.7 \ fin {array}\) |
Para calcular la circunferencia de un círculo dado un radio de 2.5 yardas, usa la fórmula\(\ C=2 \pi r\). Utilice 3.14 como aproximación para\(\ \pi\). |
La circunferencia es de 5\(\ \pi\) o aproximadamente 15.7 yardas.
Un círculo tiene un radio de 8 pulgadas. ¿Cuál es su circunferencia, redondeada a la pulgada más cercana?
- 25 pulgadas
- 50 pulgadas
- 64 pulgadas 2
- 201 pulgadas
- Contestar
-
- Incorrecto. Multiplicaste los tiempos del radio\(\ \pi\); la fórmula correcta para la circunferencia cuando se da el radio es\(\ C=2 \pi r\). La respuesta correcta es de 50 pulgadas.
- Correcto. Si el radio es de 8 pulgadas, la fórmula correcta para la circunferencia cuando se da el radio es\(\ C=2 \pi r\). La respuesta correcta es de 50 pulgadas.
- Incorrecto. Parece que cuadraste 8 y luego multiplicaste 64 por\(\ \pi\) para llegar a esta respuesta. Recuerda que la fórmula para la circunferencia cuando se da el radio es\(\ C=2 \pi r\). La respuesta correcta es de 50 pulgadas.
Área
\(\ \pi\)es un número importante en geometría. Ya lo has usado para calcular la circunferencia de un círculo. También usas\(\ \pi\) cuando estás averiguando el área de un círculo.
Para encontrar el área (\(\ A\)) de un círculo, use la fórmula:\(\ A=\pi r^{2}\)
Encuentra el área del círculo.
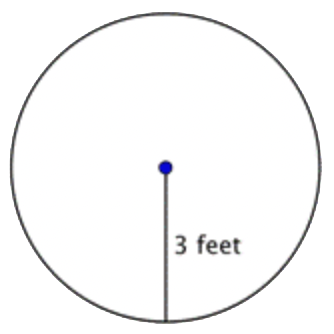
Solución
| \ (\\ begin {array} {l} A=\ pi r^ {2}\\ A=\ pi\ cdot 3^ {2}\\ A=\ pi\ cdot 9\\ A\ approx 3.14\ cdot 9\\ A\ aprox. 28.26 \ fin {array}\) |
Para encontrar el área de este círculo, usa la fórmula\(\ A=\pi r^{2}\). Recuerda escribir la respuesta en términos de unidades cuadradas, ya que estás encontrando el área. |
El área es de 9\(\ \pi\) o aproximadamente 28.26 pies 2.
Un botón tiene un diámetro de 20 milímetros. ¿Cuál es el área del botón? Usar 3.14 como aproximación de\(\ \pi\).
- 62.8 mm
- 314 mm 2
- 400 mm 2
- 1256 mm 2
- Contestar
-
- Incorrecto. Encontraste la circunferencia del botón:\(\ 20 \cdot 3.14=62.8\). Para encontrar el área, usa la fórmula\(\ A=\pi r^{2}\). La respuesta correcta es 314 mm 2
Figuras compuestas
Ahora que ya sabes calcular la circunferencia y el área de un círculo, puedes usar este conocimiento para encontrar el perímetro y el área de figuras compuestas. El truco para descubrir este tipo de problemas es identificar formas (y partes de formas) dentro de la figura compuesta, calcular sus dimensiones individuales y luego sumarlas juntas.
Por ejemplo, mira la imagen de abajo. ¿Es posible encontrar el perímetro?
El primer paso es identificar figuras más simples dentro de esta figura compuesta. Se puede descomponer en un rectángulo y un semicírculo, como se muestra a continuación.
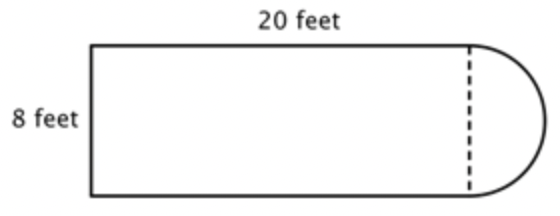
Sabes encontrar el perímetro de un rectángulo, y sabes cómo encontrar la circunferencia de un círculo. Aquí, el perímetro de los tres lados sólidos del rectángulo es\(\ 8+20+20=48 \text { feet }\). (Tenga en cuenta que solo tres lados del rectángulo se agregarán al perímetro de la figura compuesta porque el otro lado no está en un borde; ¡está cubierto por el semicírculo!)
Para encontrar la circunferencia del semicírculo, usa la fórmula\(\ C=\pi d\) con un diámetro de 8 pies, luego toma la mitad del resultado. La circunferencia del semicírculo es de 4\(\ \pi\), o aproximadamente 12.56 pies, por lo que el perímetro total es de aproximadamente 60.56 pies.
Encuentra el perímetro (a la centésima más cercana) de la figura compuesta compuesta compuesta por un semicírculo y un triángulo.
Solución
 |
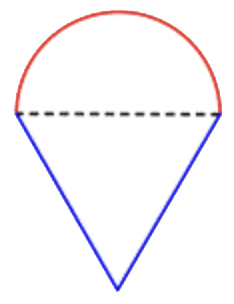Identificar formas más pequeñas dentro de la figura compuesta. Esta figura contiene un semicírculo y un triángulo. |
|
\ (\\ begin {array} {l} |
Encuentra la circunferencia del círculo. Luego divide por 2 para encontrar la circunferencia del semicírculo. |
|
Circunferencia de semicírculo\(\ =\frac{1}{2} \pi\) o aproximadamente 1.57 pulgadas \(\ 1+1+\frac{1}{2} \pi \approx 3.57 \text { inches }\)
|
Encuentra el perímetro total sumando la circunferencia del semicírculo y las longitudes de las dos patas. Dado que nuestra medición de la circunferencia del semicírculo es aproximada, el perímetro también será una aproximación. |
Aproximadamente 3.57 pulgadas
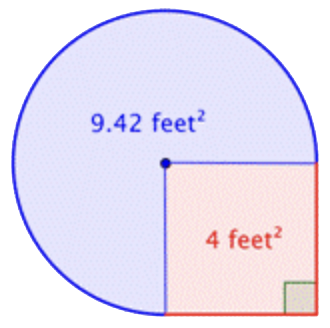
Encuentra el área de la figura compuesta, compuesta por tres cuartas partes de círculo y un cuadrado, a la centésima más cercana.
Solución
 |
Identificar formas más pequeñas dentro de la figura compuesta. Esta figura contiene una región circular y un cuadrado. Si encuentras el área de cada uno, puedes encontrar el área de toda la figura. |
|
\ (\\ begin {array} {l} |
Encuentra el área de la plaza. |
|
\ (\\ begin {array} {l} |
Encuentra el área de la región circular. El radio es de 2 pies. |
| \ (\\ begin {array} {c} \ text {Área de región} =\ frac {3} {4}\ cdot4\ pi\\ =3\ pi\ \\ approx3\ cdot3.14\ text {ft} ^2\ \ text {Esto es aproximadamente} 9.42\ text {pies} ^2 \ end {array}\) |
Tenga en cuenta que la región es\(\ \frac{3}{4}\) de un círculo completo, por lo que debe multiplicar el área del círculo por\(\ \frac{3}{4}\). Utilice 3.14 como aproximación para\(\ \pi\). |
|
\(\ 4 \text { feet}^{2}+3 \pi \text { feet}^{2}=\text { approximately } 13.42 \text { feet}^{2}\) |
Sumar las dos regiones juntas. Dado que su medida del área de la circular es aproximada, el área de la figura será una aproximación también. |
El área es aproximadamente\(\ 13.42 \text { feet }^{2}\).
¿Cuál es el área (a la centésima más cercana) de la figura que se muestra a continuación? (Ambas regiones redondeadas son semicírculos).
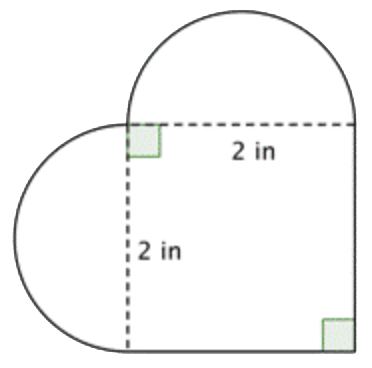
- 16.56 en 2
- 7.14 en 2
- 4 en 2
- 3.14 en 2
- Contestar
-
Resumen
Los círculos son una forma geométrica importante. La distancia alrededor de un círculo se llama circunferencia, y el espacio interior de un círculo se llama área. El cálculo de la circunferencia y el área de un círculo requiere un número llamado pi (\(\ \pi\)), que es un decimal no terminante y no repetitivo. Pi a menudo se aproxima por los valores 3.14 y\(\ \frac{22}{7}\). Puede encontrar el perímetro o área de formas compuestas, incluidas las formas que contienen secciones circulares, aplicando las fórmulas de circunferencia y área donde corresponda.