7.2.2: Perímetro y Área
- Page ID
- 111353
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Encuentra el perímetro de un polígono.
- Encuentra el área de un polígono.
- Encuentra el área y perímetro de polígonos no estándar.
Introducción
Perímetro y área son dos temas matemáticos importantes y fundamentales. Te ayudan a cuantificar el espacio físico y también proporcionan una base para matemáticas más avanzadas que se encuentran en álgebra, trigonometría y cálculo. El perímetro es una medida de la distancia alrededor de una forma y el área nos da una idea de cuánta superficie cubre la forma.
El conocimiento de área y perímetro es aplicado prácticamente por personas a diario, como arquitectos, ingenieros y diseñadores gráficos, y es matemática que es muy necesaria para la gente en general. Entender cuánto espacio tienes y aprender a encajar las formas exactamente te ayudará cuando pintas una habitación, compras una casa, remodelas una cocina o construyes una terraza.
Perimetral
El perímetro de una forma bidimensional es la distancia alrededor de la forma. Se puede pensar en envolver una cuerda alrededor de un triángulo. La longitud de esta cuerda sería el perímetro del triángulo. O caminando por el exterior de un parque, caminas a lo lejos del perímetro del parque. A algunas personas les resulta útil pensar “perimetral” porque el borde de un objeto es su borde y perimetral tiene la palabra “borde” en él.
Si la forma es un polígono, entonces puedes sumar todas las longitudes de los lados para encontrar el perímetro. Tenga cuidado de asegurarse de que todas las longitudes se midan en las mismas unidades. Se mide el perímetro en unidades lineales, que es unidimensional. Ejemplos de unidades de medida para la longitud son pulgadas, centímetros o pies.
Encuentra el perímetro de la figura dada. Todas las medidas indicadas son pulgadas.

Solución
| \(\ P=5+3+6+2+3+3\) | Dado que todos los lados se miden en pulgadas, solo agrega las longitudes de los seis lados para obtener el perímetro. |
| \(\ P=22 \text { inches }\) | Recuerda incluir unidades. |
Esto significa que una cuerda bien envuelta que recorre toda la distancia alrededor del polígono mediría 22 pulgadas de largo.
Encuentra el perímetro de un triángulo con lados de 6 cm, 8 cm y 12 cm.
Solución
| \(\ P=6+8+12\) | Ya que todos los lados se miden en centímetros, solo agrega las longitudes de los tres lados para obtener el perímetro. |
\(\ P=26 \text { centimeters }\)
En ocasiones, necesitas usar lo que sabes de un polígono para encontrar el perímetro. Veamos el rectángulo en el siguiente ejemplo.
Un rectángulo tiene una longitud de 8 centímetros y un ancho de 3 centímetros. Encuentra el perímetro.

Solución
| \(\ P=3+3+8+8\) | Al tratarse de un rectángulo, los lados opuestos tienen las mismas longitudes, 3 cm. y 8 cm. Suma las longitudes de los cuatro lados para encontrar el perímetro. |
\(\ P=22 \mathrm{~cm}\)
Observe que el perímetro de un rectángulo siempre tiene dos pares de lados de igual longitud. En el ejemplo anterior también podrías haber escrito\(\ P=2(3)+2(8)=6+16=22 \mathrm{~cm}\). La fórmula para el perímetro de un rectángulo suele escribirse como\(\ P=2 l+2 w\), donde\(\ l\) está la longitud del rectángulo y\(\ w\) es el ancho del rectángulo.
Área de Paralelogramos
El área de una figura bidimensional describe la cantidad de superficie que cubre la forma. Se mide el área en unidades cuadradas de un tamaño fijo. Ejemplos de unidades de medida cuadradas son pulgadas cuadradas, centímetros cuadrados o millas cuadradas. Al encontrar el área de un polígono, se cuenta cuántos cuadrados de cierto tamaño cubrirán la región dentro del polígono.
Veamos un cuadrado de 4 por 4.

Se puede contar que hay 16 cuadrados, por lo que el área es de 16 unidades cuadradas. Contar 16 cuadrados no lleva demasiado tiempo, pero ¿qué pasa con encontrar el área si este es un cuadrado más grande o las unidades son más pequeñas? Podría llevar mucho tiempo contar.
Afortunadamente, puedes usar la multiplicación. Ya que hay 4 filas de 4 cuadrados, ¡puedes multiplicar\(\ 4 \cdot 4\) para obtener 16 cuadrados! Y esto puede generalizarse a una fórmula para encontrar el área de un cuadrado con cualquier longitud,\(\ s\):\(\ \text { Area }=s \cdot s=s^{2}\).

Puedes escribir “\(\ \mathrm{in}^{2}\)” para pulgadas cuadradas y “\(\ \mathrm{ft}^{2}\)” para pies cuadrados.
Para ayudarte a encontrar el área de las diferentes categorías de polígonos, los matemáticos han desarrollado fórmulas. Estas fórmulas te ayudan a encontrar la medición más rápidamente que simplemente contando. Las fórmulas que vas a ver están todas desarrolladas a partir del entendimiento de que estás contando el número de unidades cuadradas dentro del polígono. Veamos un rectángulo.

Se pueden contar los cuadrados individualmente, pero es mucho más fácil multiplicar 3 por 5 para encontrar el número más rápidamente. Y, de manera más general, el área de cualquier rectángulo se puede encontrar multiplicando longitud por ancho.
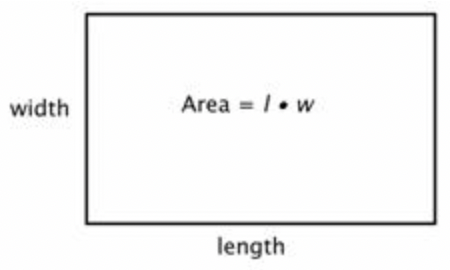
Un rectángulo tiene una longitud de 8 centímetros y un ancho de 3 centímetros. Encuentra la zona.

Solución
| \(\ A=l \cdot w\) | Comience con la fórmula para el área de un rectángulo, que multiplica la longitud por el ancho. |
| \(\ A=8 \cdot 3\) | Sustituye 8 por el largo y 3 por el ancho. |
| \(\ A=24 \mathrm{~cm}^{2}\) | Asegúrese de incluir las unidades, en este caso centímetros cuadrados. |
Se necesitarían 24 cuadrados, cada uno de 1 centímetro de lado, para cubrir este rectángulo.
La fórmula para el área de cualquier paralelogramo (recuerde, un rectángulo es un tipo de paralelogramo) es la misma que la de un rectángulo:\(\ \text { Area }=l \cdot w\). Observe en un rectángulo, el largo y el ancho son perpendiculares. Esto también debería ser cierto para todos los paralelogramos. A menudo se usa base (\(\ b\)para la longitud (de la base\(\ h\)) y altura () para el ancho de la línea perpendicular a la base. Entonces la fórmula para un paralelogramo generalmente se escribe,\(\ A=b \cdot h\).

Encuentra el área del paralelogramo.

Solución
| \(\ A=b \cdot h\) | Comience con la fórmula para el área de un paralelogramo: |
| \(\ A=4 \cdot 2\) |
\(\ \text { Area }=\text { base } \cdot \text { height }\). Sustituir los valores en la fórmula. |
| \(\ A=8\) | Multiplicar. |
El área del paralelogramo es 8\(\ \mathrm{ft}^{2}\).
Encuentra el área de un paralelogramo con una altura de 12 pies y una base de 9 pies.
- \(\ 21 \mathrm{ft}^{2}\)
- \(\ 54 \mathrm{ft}^{2}\)
- \(\ 42 \mathrm{ft}\)
- \(\ 108 \mathrm{ft}^{2}\)
- Responder
-
- Incorrecto. Parece que agregaste las dimensiones; recuerda que para encontrar el área, multiplicas la base por la altura. La respuesta correcta es\(\ 108 \mathrm{ft}^{2}\).
- Incorrecto. Parece que multiplicaste la base por la altura y luego dividiste por 2. Para encontrar el área de un paralelogramo, multiplicas la base por la altura. La respuesta correcta es\(\ 108 \mathrm{ft}^{2}\).
- Incorrecto. Parece que agregaste\(\ 12+12+9+9\). Esto te daría el perímetro de un rectángulo de 12 por 9. Para encontrar el área de un paralelogramo, multiplicas la base por la altura. La respuesta correcta es\(\ 108 \mathrm{ft}^{2}\).
- Correcto. La altura del paralelogramo es 12 y la base del paralelogramo es 9; el área es 12 veces 9, o\(\ 108 \mathrm{ft}^{2}\).
Área de Triángulos y Trapezoides
La fórmula para el área de un triángulo se puede explicar mirando un triángulo rectángulo. En la imagen de abajo hay un rectángulo con la misma altura y base que el triángulo original. ¡El área del triángulo es la mitad del rectángulo!

Dado que el área de dos triángulos congruentes es la misma que el área de un rectángulo, se puede llegar a la fórmula\(\ \text { Area }=\frac{1}{2} b \cdot h\) para encontrar el área de un triángulo.
Cuando se utiliza la fórmula para que un triángulo encuentre su área, es importante identificar una base y su altura correspondiente, que es perpendicular a la base.

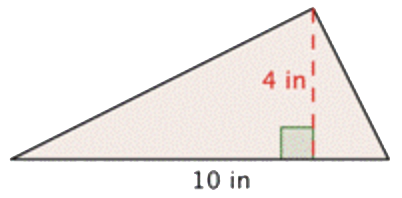
Un triángulo tiene una altura de 4 pulgadas y una base de 10 pulgadas. Encuentra la zona.
Solución
| \(\ A=\frac{1}{2} b h\) | Comienza con la fórmula para el área de un triángulo. |
| \(\ A=\frac{1}{2} \cdot 10 \cdot 4\) | Sustituye 10 por la base y 4 por la altura. |
|
\(\ A=\frac{1}{2} \cdot 40\) \(\ A=20\) |
Multiplicar. |
\(\ A=20 \text { in }^{2}\)
Ahora veamos el trapecio. Para encontrar el área de un trapecio, tomar la longitud promedio de las dos bases paralelas y multiplicar esa longitud por la altura:\(\ A=\frac{\left(b_{1}+b_{2}\right)}{2} h\).
A continuación se proporciona un ejemplo. Observe que la altura de un trapecio siempre será perpendicular a las bases (igual que cuando encuentre la altura de un paralelogramo).
Encuentra el área del trapecio.

Solución
| \(\ A=\frac{\left(b_{1}+b_{2}\right)}{2} h\) | Comienza con la fórmula para el área de un trapecio. |
| \ (\\ begin {array} {c} A=\ frac {(4+7)} {2}\ cdot 2\\ A=\ frac {11} {2}\ cdot 2\ A=11 \ end {array}\) |
Sustituye 4 y 7 por las bases y 2 por la altura, y encuentra\(\ A\). |
El área del trapecio es\(\ 11 \mathrm{~cm}^{2}\).
Utilice las siguientes fórmulas para encontrar las áreas de diferentes formas.
cuadrado:\(\ A=s^{2}\)
rectángulo:\(\ A=l \cdot w\)
paralelogramo:\(\ A=b \cdot h\)
triángulo:\(\ A=\frac{1}{2} b \cdot h\)
trapecio:\(\ A=\frac{\left(b_{1}+b_{2}\right)}{2} h\)
Trabajando con Perímetro y Área
A menudo es necesario encontrar el área o perímetro de una forma que no sea un polígono estándar. Los artistas y arquitectos, por ejemplo, suelen tratar con formas complejas. Sin embargo, incluso las formas complejas pueden considerarse compuestas por formas más pequeñas y menos complicadas, como rectángulos, trapecios y triángulos.
Para encontrar el perímetro de formas no estándar, aún encuentras la distancia alrededor de la forma al sumar la longitud de cada lado.
Encontrar el área de formas no estándar es un poco diferente. Es necesario crear regiones dentro de la forma para las que pueda encontrar el área y agregar estas áreas juntas. Echa un vistazo a cómo se hace esto a continuación.
Encuentra el área y perímetro del polígono.

Solución
| \ (\\ begin {array} {r} P=18+6+3+11+9.5+6+6\\ P=59.5\ mathrm {~cm} \ end {array}\) |
Para encontrar el perímetro, sumar las longitudes de los lados. Comience en la parte superior y trabaje en sentido horario alrededor de la forma. |
|
Área de Polígono = (Área de A) + (Área de B) |
Para encontrar el área, divida el polígono en dos regiones separadas y más simples. El área de todo el polígono será igual a la suma de las áreas de las dos regiones. |
| \ (\\ begin {array} {r} \ text {Área de Región} a=L\ cdot w\\ =18\ cdot 6\\ =108 \ end {array}\) |
La región A es un rectángulo. Para encontrar el área, multiplica la longitud (18) por la anchura (6). El área de la Región A es de 108 cm 2. |
| \ (\\ begin {array} {r} \ text {Área de Región}\ mathrm {B} =\ frac {1} {2} b\ cdot h \\ =\ frac {1} {2}\ cdot 9\ cdot 9\\ =\ frac {1} {2}\ cdot 81\\ =40.5 \ end { matriz}\) |
La región B es un triángulo. Para encontrar el área, usa la fórmula\(\ \frac{1}{2} b h\), donde la base es 9 y la altura es 9. |
| \(\ 108 \mathrm{~cm}^{2}+40.5 \mathrm{~cm}^{2}=148.5 \mathrm{~cm}^{2}\) |
El área de la Región B es de 40.5 cm 2. Sumar las regiones juntas. |
\ (\\ begin {array} {c}
\ text {Perímetro} =59.5\ mathrm {~cm}\
\ texto {Área} =148.5\ mathrm {~cm} ^ {2}
\ end {array}\)
También puedes usar lo que sabes sobre perímetro y área para ayudar a resolver problemas sobre situaciones como comprar cercas o pintar, o determinar qué tan grande se necesita una alfombra en la sala de estar. Aquí hay un ejemplo de esgrima.
Rosie está plantando un jardín con las dimensiones que se muestran a continuación. Ella quiere poner una capa delgada y uniforme de mantillo sobre toda la superficie del jardín. El mantillo cuesta $3 el pie cuadrado. ¿Cuánto dinero tendrá que gastar en mantillo?

Solución
 |
Esta forma es una combinación de dos formas más simples: un rectángulo y un trapecio. Encuentra el área de cada uno. |
| \ (\\ begin {array} {c} a=L\ cdot w\\ A=8\ cdot 4\\ A=32\ mathrm {ft} ^ {2} \ end {array}\) |
Encuentra el área del rectángulo. |
| \ (\\ comenzar {matriz} {c} A=\ frac {\ izquierda (b_ {1} +b_ {2}\ derecha)} {2} h\\ A=\ frac {(14+8)} {2}\ cdot 4\\ A=\ frac {22} {2}\ cdot 4\ A=11\ cdot 4\ A=44\ mathrm {ft} ^ {2} \ end {array}\) |
Encuentra el área del trapecio. |
| \(\ 32 \mathrm{ft}^{2}+44 \mathrm{ft}^{2}=76 \mathrm{ft}^{2}\) | Agregar las medidas. |
| \(\ 76 \mathrm{ft}^{2} \cdot \$ 3=\$ 228\) | Multiplica por $3 para saber cuánto tendrá que gastar Rosie. |
Rosie gastará 228 dólares para cubrir su jardín con mantillo.
Encuentra el área de la forma que se muestra a continuación.

- \(\ 11 \mathrm{ft}^{2}\)
- \(\ 18 \mathrm{ft}^{2}\)
- \(\ 20.3 \mathrm{ft}\)
- \(\ 262.8 \mathrm{ft}^{2}\)
- Responder
-
- Correcto. Esta forma es un trapecio, por lo que puedes usar la fórmula\(\ A=\frac{\left(b_{1}+b_{2}\right)}{2} h\) para encontrar el área:\(\ A=\frac{(2+9)}{2} \cdot 2\).
- Incorrecto. Parece que multiplicaste 2 por 9 para obtener\(\ 18 \mathrm{ft}^{2}\); esto funcionaría si la forma fuera un rectángulo. Sin embargo, esta forma es un trapecio, así que usa la fórmula\(\ A=\frac{\left(b_{1}+b_{2}\right)}{2} h\). La respuesta correcta es\(\ 11 \mathrm{ft}^{2}\).
- Incorrecto. Parece que agregaste todas las dimensiones juntas. Esto te daría el perímetro. Para encontrar el área de un trapecio, usa la fórmula\(\ A=\frac{\left(b_{1}+b_{2}\right)}{2} h\). La respuesta correcta es\(\ 11 \mathrm{ft}^{2}\).
- Incorrecto. Parece que multiplicaste todas las dimensiones juntas. Esta forma es un trapecio, por lo que usas la fórmula\(\ A=\frac{\left(b_{1}+b_{2}\right)}{2} h\). La respuesta correcta es\(\ 11 \mathrm{ft}^{2}\).
Resumen
El perímetro de una forma bidimensional es la distancia alrededor de la forma. Se encuentra sumando todos los lados (siempre y cuando todos sean la misma unidad). El área de una forma bidimensional se encuentra contando el número de cuadrados que cubren la forma. Se han desarrollado muchas fórmulas para encontrar rápidamente el área de polígonos estándar, como triángulos y paralelogramos.



