8.3.1: Uso y mal uso de las representaciones gráficas
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Identificar qué tipo de gráfico representa mejor los datos para una situación dada.
- Explique cómo las gráficas pueden llevar a una mala interpretación de los datos.
Introducción
Además de los gráficos de barras, histogramas y gráficos circulares (gráficos circulares), hay otras gráficas que los estadísticos utilizan para representar datos y analizar lo que muestran. Pero hay que tener cuidado a la hora de crear y leer gráficas. Si no se crean cuidadosamente, pueden ser engañosos, y a veces la gente los hace engañosos a propósito.
Elegir una Gráfica
Elegir qué tipo de gráfico usar para representar un conjunto de datos específico requiere algo de prueba y error. Y, a veces, hay más de un tipo apropiado de gráfico que puedes usar. Lo que elijas depende de la forma en que quieras presentar tus datos, así como de tus propias preferencias personales. Los programas modernos de hojas de cálculo como Excel son muy flexibles en la creación de diferentes tipos de gráficos; con solo un par de clics, puede ver los datos representados como un gráfico de barras, un gráfico de líneas o un gráfico circular. A partir de ahí, puedes elegir cuál pinta mejor el cuadro que quieres mostrar.
Dado que a menudo hay más de una forma de graficar un conjunto de datos, veamos algunos ejemplos y pensemos en las diferentes posibilidades que tenemos disponibles.
Un escritor beisbolero quiere crear una gráfica que muestre el total de éxitos para los jugadores con mayor número de éxitos en la primera mitad de la temporada de beisbol. Estos jugadores tienen el siguiente número de hits: 86, 88, 90, 90, 97, 99, 102 y 106. ¿Qué tipo de gráfica debe utilizar el escritor para representar los datos?
Solución
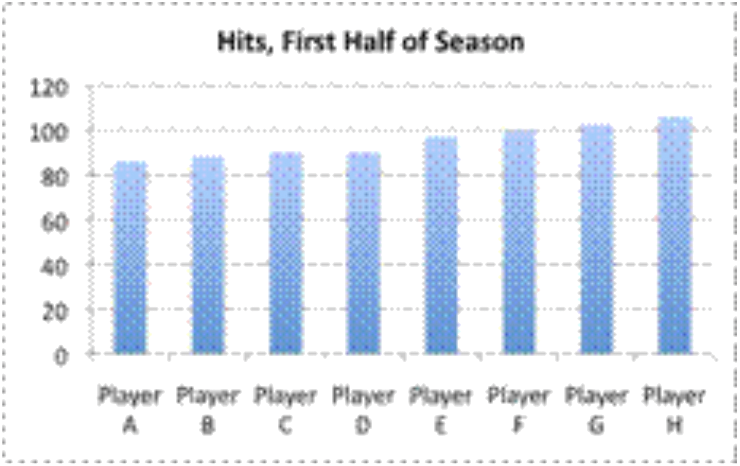 |
El conjunto de datos contiene información sobre los totales de aciertos de 8 jugadores. Ya sea un gráfico de barras o un pictograma podrían ayudar a mostrar el número total de hits que cada jugador tuvo en comparación con los otros jugadores. |
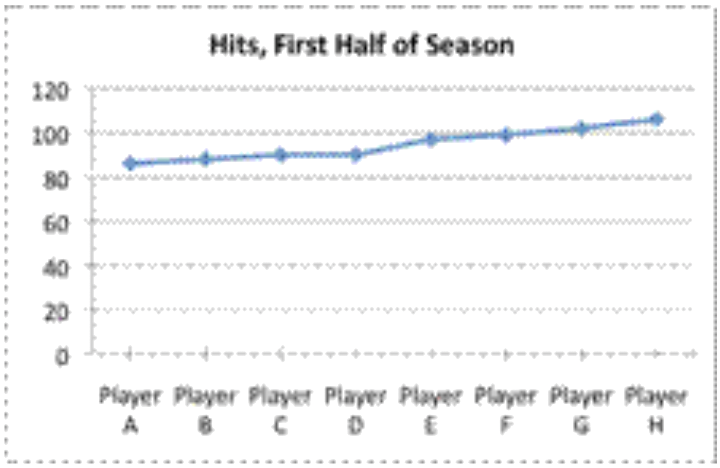 |
Un gráfico de líneas no sería apropiado, ya que los datos no son continuos. No hay datos “entre” los totales de aciertos de cada jugador. |
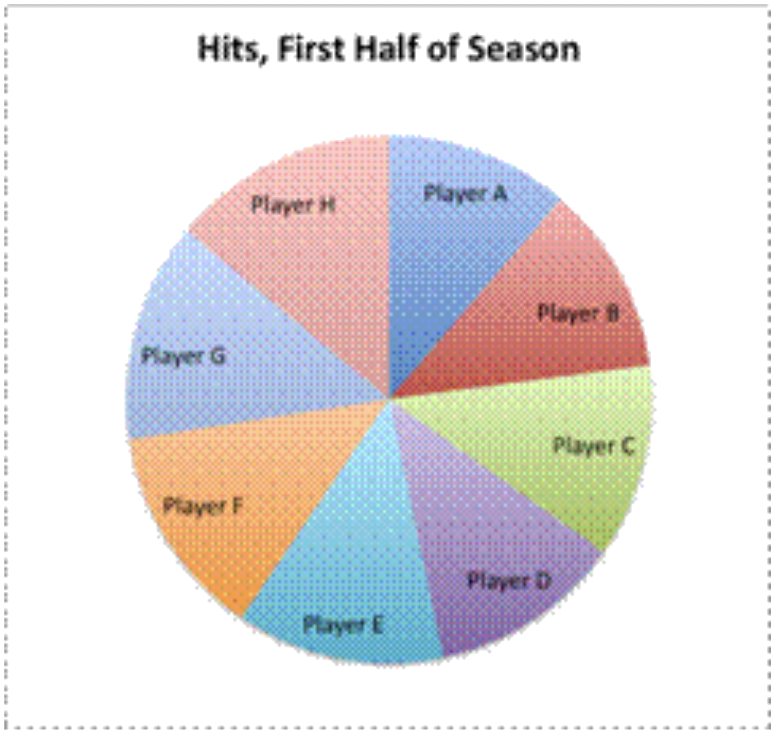 |
Un gráfico circular tampoco tiene sentido, a menos que el escritor quiera mostrar el porcentaje de hits que cada jugador tiene del número total de hits. Pero esos datos no serían de gran ayuda si el escritor solo quiere mostrar la cantidad total de éxitos. |
Un gráfico de barras o pictografía funcionaría mejor aquí. (Un pictograma puede ser preferible para una pequeña cantidad de datos, y un gráfico de barras puede ser preferible para muchos datos).
El escritor podría usar una trama de tallo y hoja para mostrar la distribución de datos numéricos, pero este tipo de gráfica no es tan efectiva para mostrar la relación entre cada jugador y el número de hits que tiene. Una trama de caja y bigotes, que muestra la mitad de un conjunto de datos, no es útil aquí ya que al escritor le interesan los totales de aciertos, no el número promedio de aciertos o la propagación de los datos.
Un estadístico está recopilando datos sobre la frecuencia con la que los adultos acuden al odontólogo. Encuesta a 128 personas y encuentra la siguiente información.
- Menos de 1 vez al año: 28 encuestados
- 1 vez al año: 51 encuestados
- 2 veces al año: 42 encuestados
- Más de 2 veces al año: 7 encuestados
En una presentación ante odontólogos, sobre todo quiere destacar a la población que visita al odontólogo menos de 1 vez al año. ¿Qué tipo de gráfica debe utilizar para representar los datos?
Solución
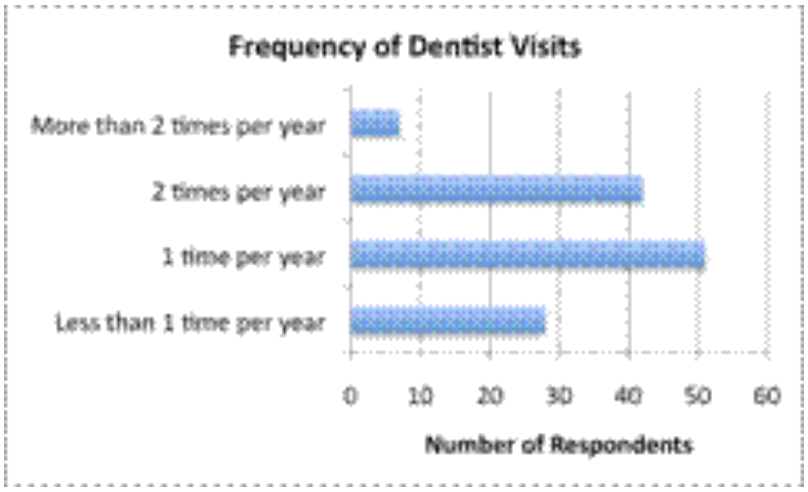 |
Para mostrar sus hallazgos, la estadística podría usar un par de gráficas diferentes. Un gráfico de barras estaría bien para usar aquí ya que los datos son categóricos. Ella ha agrupado sus hallazgos en 4 categorías. |
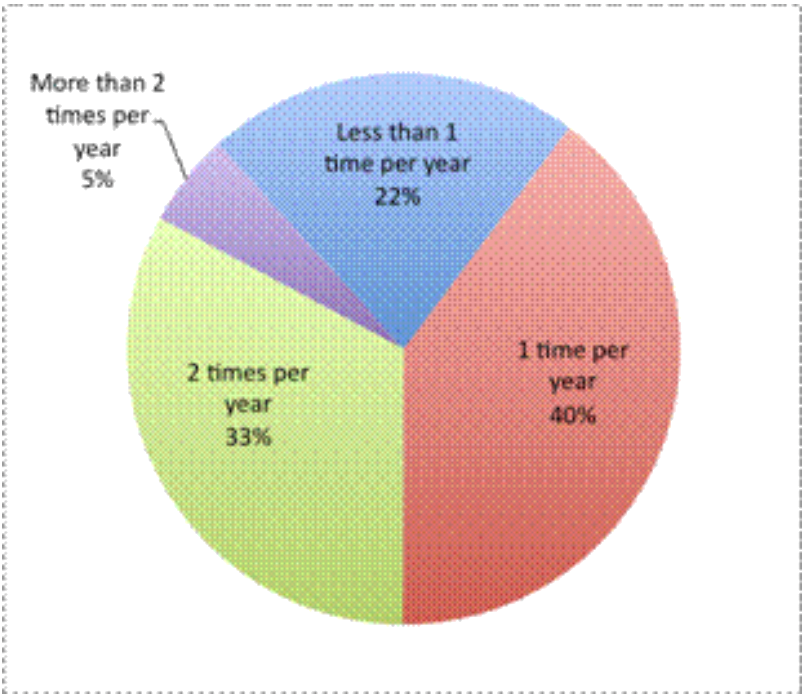 |
Un gráfico circular puede ser aún mejor. Al estadístico le interesa el porcentaje o participación de las personas que respondieron a cada pregunta. Un gráfico circular permite una comparación fácil entre las categorías encuestadas. |
Un gráfico circular es lo mejor, pero también sería aceptable un gráfico de barras.
Al igual que con el primer ejemplo, las parcelas de tallo y hoja y las parcelas de caja y bigotes no son útiles aquí. Al estadístico no le interesa la cantidad promedio de veces que una persona acude al dentista cada año. Tampoco sería apropiado un gráfico de líneas, ya que los datos no son continuos.
Un planificador de parques de diversiones quiere comprender mejor la distribución de los tiempos de espera que la gente experimenta mientras espera un viaje popular. En el parque un día, le pregunta a 15 personas aleatorias sobre el tiempo que tuvieron que esperar (en minutos).
12, 3, 2, 10, 12, 0, 2, 0, 8, 5, 4, 0, 7, 4, 6
¿Qué tipo de gráfica proporciona la mejor representación visual de este conjunto de datos: una gráfica circular, una gráfica de caja y bigotes o una gráfica de barras?
Solución
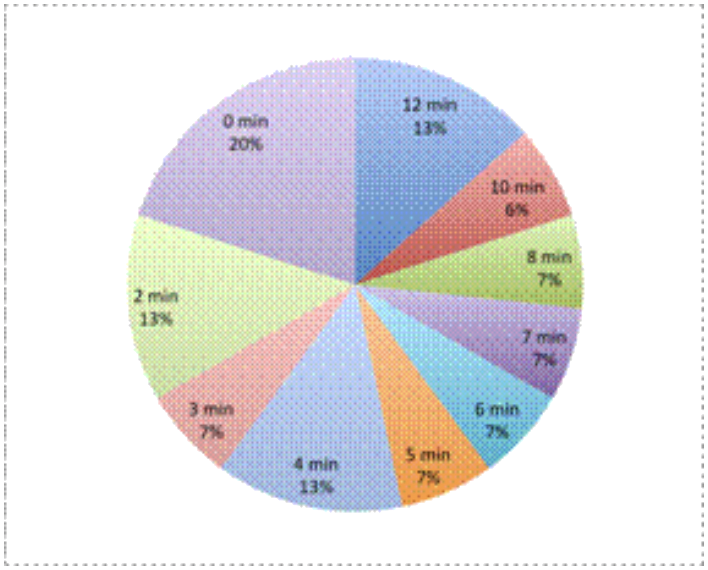 |
La idea clave aquí es que el planificador quiere entender la distribución de los tiempos de espera. Una gráfica circular no muestra la distribución. El planificador podría crear una gráfica circular (como la de la izquierda) que muestre el porcentaje de personas que esperaron diferentes cantidades de tiempo, pero esto no le ayuda a entender la distribución de los datos. |
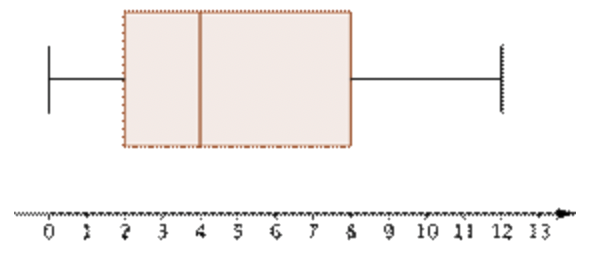 |
Crear una trama de caja y bigotes sería más útil. Este tipo de gráfica mostraría la distribución de manera más efectiva, como se ve a la izquierda. La mitad de la gente esperó entre 2 y 8 minutos para el viaje. |
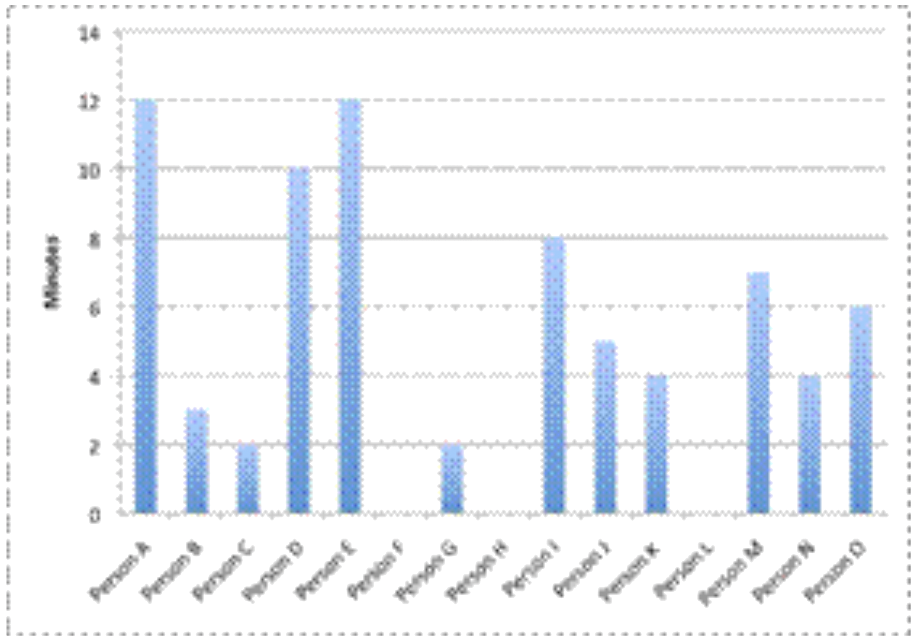 |
Un gráfico de barras puede mostrar la longitud que cada persona esperó, pero no muestra mucho sobre la distribución de los tiempos de espera. |
| Una trama de caja y bigotes es lo mejor. | En definitiva, la trama de caja y bigotes da la mayor información sobre la distribución, por lo que es la más útil. |
Un oceanógrafo quiere hacer una gráfica que muestre la altura (en centímetros) de un coral específico durante el periodo de 2 años. ¿Qué tipo de gráfica es la más adecuada?
- Gráfico circular
- Trama de caja y bigotes
- Gráfico de líneas
- Parcela de tallo y hoja
- Responder
-
- Gráfico circular
Incorrecto. Un gráfico circular se usa a menudo para mostrar partes de un todo, no cambios con el tiempo. La respuesta correcta es un gráfico de líneas.
- Trama de caja y bigotes
Incorrecto. Se utiliza una gráfica de caja y bigotes para mostrar la mitad de un conjunto de datos; no revela mucho sobre el crecimiento a lo largo del tiempo. La respuesta correcta es un gráfico de líneas.
- Gráfico de líneas
Correcto. Un gráfico de líneas que mapea la altura a lo largo del eje y y el tiempo a lo largo del eje x es el tipo de gráfico más apropiado para esta situación.
- Parcela de tallo y hoja
Incorrecto. Se utiliza una gráfica de tallo y hoja para mostrar la propagación de un conjunto de datos; no revela mucho sobre el crecimiento a lo largo del tiempo. La respuesta correcta es un gráfico de líneas.
- Gráfico circular
Gráficas engañosas
Como has visto, los gráficos proporcionan una forma visual de representar conjuntos de datos. Sin embargo, las imágenes pueden ser engañosas, por lo que también necesitas saber identificar gráficas que parecen mostrar algo diferente a lo que dicen los datos. Esto puede ser por descuido o puede hacerse a propósito. A continuación se presentan algunas preguntas generales a tener en cuenta a medida que lee las gráficas.
- ¿Las gráficas están suficientemente etiquetadas?
- ¿Cuál es la escala?
- ¿La gráfica muestra una imagen completa de los datos, o solo una imagen seleccionada?
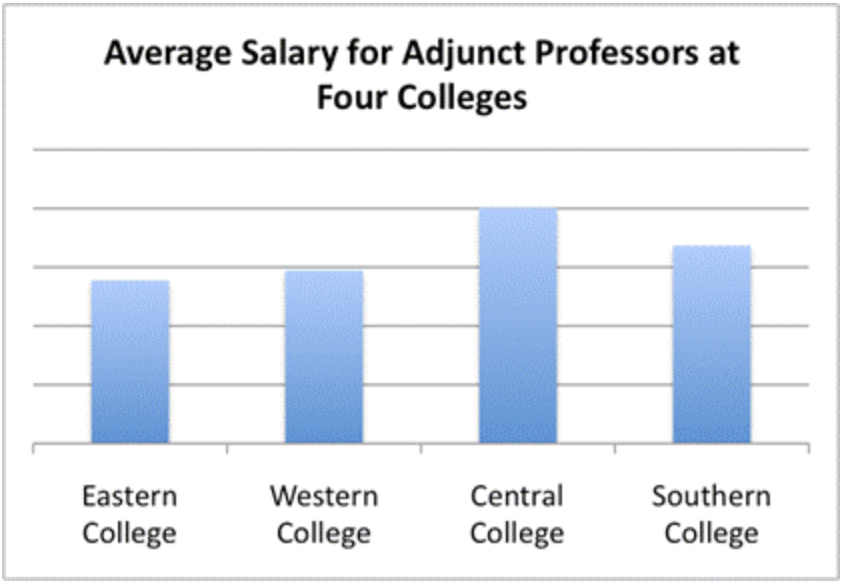
Mira la gráfica que sigue. El título establece “Salario promedio para profesores adjuntos en cuatro colegios”, y cuatro barras aparecen en la gráfica. Se puede decir qué colegios se están comparando, pero no se le da información sobre la escala que se está utilizando. El gráfico hace parecer que el salario promedio para Profesores Adjuntos en Central College es mucho mayor que el de Eastern College, pero sin una escala, no se puede saber con certeza. (Sí sabes que el salario es mayor; simplemente no sabes cuánto más alto.) Para que esta gráfica sea menos engañosa, se debe incluir un eje y con información salarial.
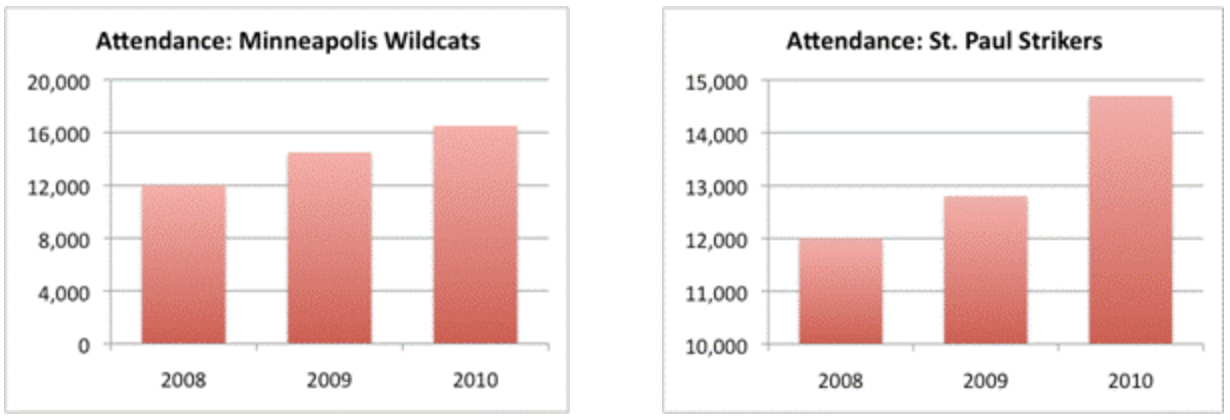
Incluso cuando ambos ejes están presentes y etiquetados correctamente, las representaciones gráficas de los datos pueden ser engañosas. Esto se muestra en el conjunto de gráficas de asistencia que siguen.
En la gráfica de la izquierda, la escala comienza en 0 y va a 20,000. El gráfico en sí muestra que la asistencia a los juegos de Minneapolis Wildcats ha aumentado constantemente cada año desde 2008, superando en 2010 con poco más de 16,000.
Ahora mira la gráfica de la derecha. Parece demostrar que la asistencia a los juegos de St. Paul Strikers ha aumentado aún más dramáticamente: el listón para 2010 es más del doble de alto que el de 2008. Al mirar estas dos gráficas, se puede concluir que los Strikers han sido el equipo más popular recientemente, ya que la altura de las barras parece indicar que su asistencia ha crecido más rápido que la de los Wildcats.
Pero fíjense algo interesante: la escala de la gráfica de Strikers es muy diferente. ¡Comienza en 10,000! Esto pinta una imagen sesgada de los datos cuando se compara con la gráfica Wildcats, que comienza en 0. Y al examinar los datos reales (la asistencia real, no solo la altura de las barras), se puede decir que la asistencia es en realidad mayor en los juegos de Wildcats. En 2010, por ejemplo, la asistencia de Wildcats es un poco más de 16,000, mientras que la asistencia a los juegos de Strikers es inferior a 15 mil.
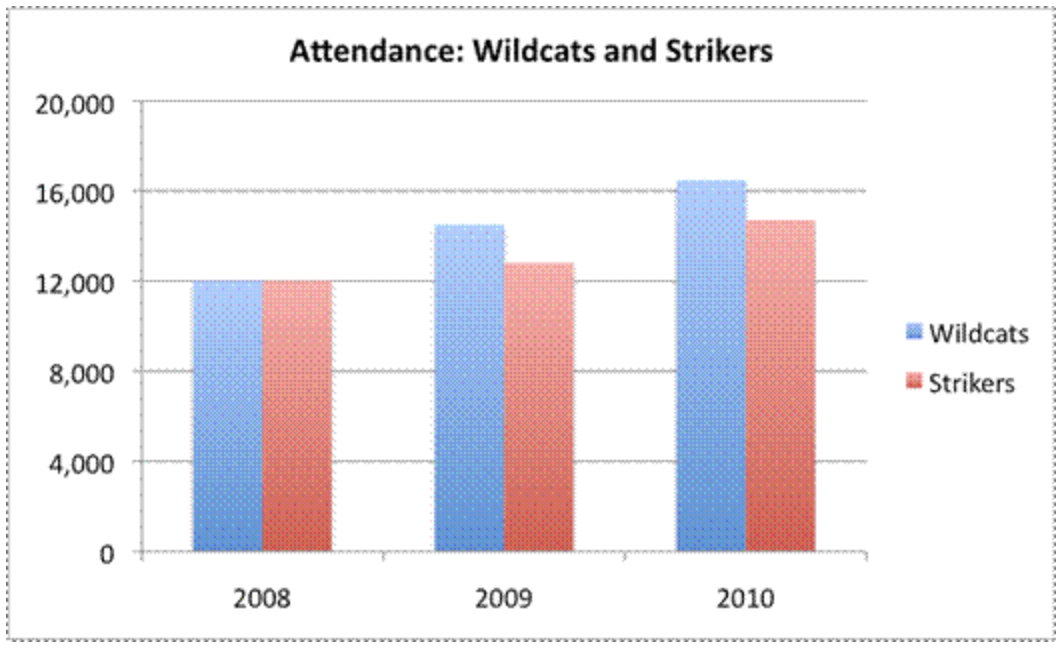
Esto trae a colación un punto importante. Cuando se utilizan gráficos para comparar conjuntos de datos, las escalas deben ser consistentes; de lo contrario, es muy difícil comparar los datos en sí. Como se puede decir de las dos gráficas anteriores, cambiar la escala de una gráfica puede cambiar drásticamente la forma en que se ve y la impresión que hace la gráfica.
Una representación más honesta de los datos de asistencia se puede encontrar en un gráfico de doble barra, donde las cifras de asistencia de ambos equipos se mapean lado a lado usando la misma escala. Mira los resultados a continuación. Ahora es claro que la asistencia de los Wildcats es mayor que la asistencia de los Strikers.
El gráfico circular aquí es otro ejemplo de una representación engañosa. Los porcentajes reales de personas que respondieron a cada pregunta no están disponibles, y el espectador tiene que interpretar los datos en función del tamaño de las secciones. A primera vista, esta gráfica parece estar mostrando que muchos votantes parecen estar favoreciendo al Candidato A, ya que la sección “Sí” es muy grande.
Parte de la razón por la que esta sección aparece grande es porque la gráfica ha sido creada para que se vea grande. El gráfico circular se presenta en forma tridimensional, y los datos que están más destacados en la gráfica (la porción “Sí”) aparecen los más destacados. El creador de esta gráfica espera que esta gráfica te haga pensar que ¡el Candidato A es muy popular!
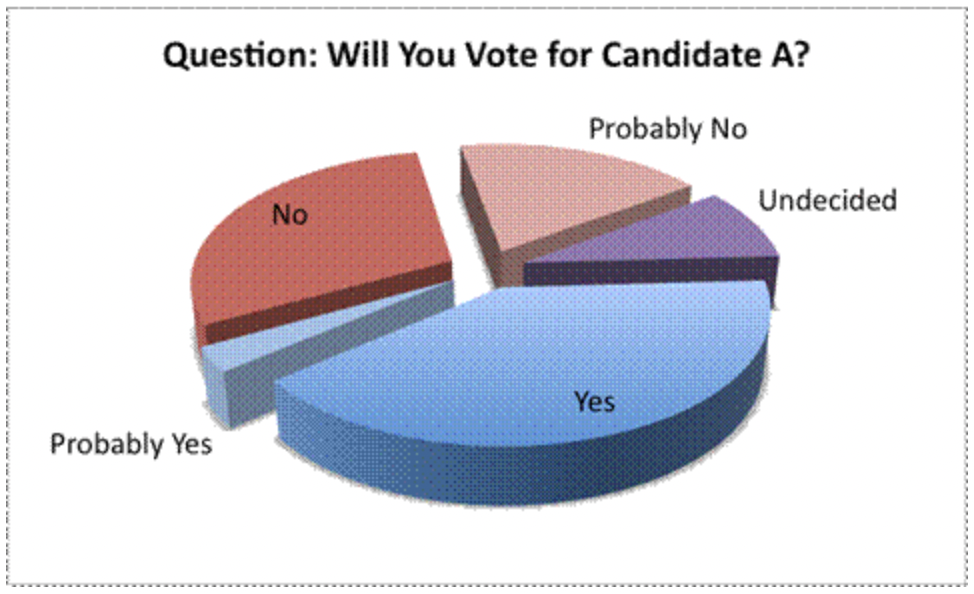
Sin embargo, en una inspección más cercana, los datos no parecen apoyar esta contención. Combinar las secciones “Sí” y “Probablemente Sí” es aproximadamente igual a combinar las secciones “No” y “Probablemente No”, lo que significa que el candidato no es tan popular como sugeriría esta representación. De hecho, alguien que no quería que este candidato apareciera favorable podría haber representado los datos usando la siguiente gráfica. Observe las diferentes posiciones de las secciones “No” y “Probablemente No”, así como los colores consistentes.
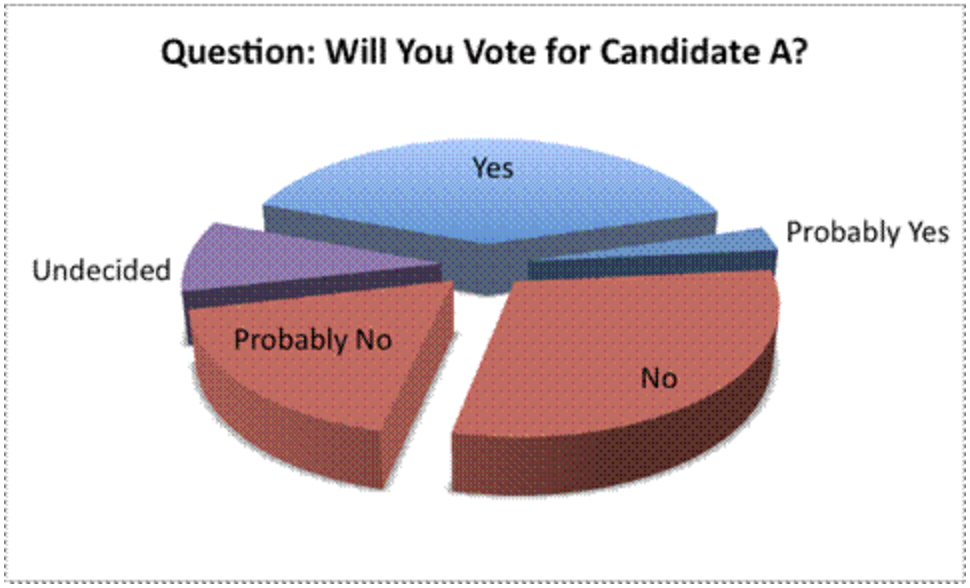
¡Observe cómo la perspectiva y el color marcan la diferencia en la visualización y análisis de datos!
A continuación se presenta una forma más honesta de representar estos datos. En esta gráfica, la gráfica circular se muestra desde arriba, y se incluyen los porcentajes reales.
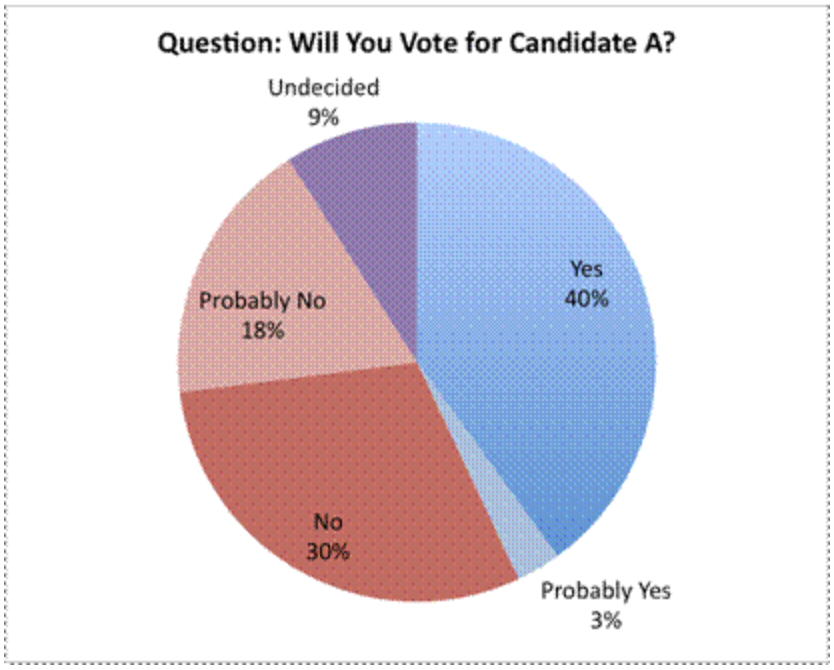
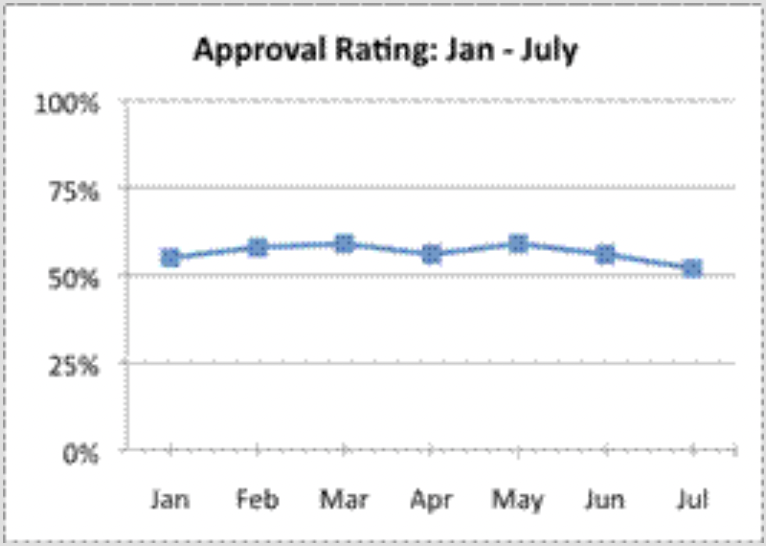
Los resultados de una encuesta que mide la calificación de aprobación de un político se muestran en la siguiente tabla.
| Fecha | Calificación de aprobación (%) |
| enero | 55% |
| febrero | 58% |
| marzo | 59% |
| abril | 56% |
| Mayo | 59% |
| junio | 56% |
| julio | 52% |
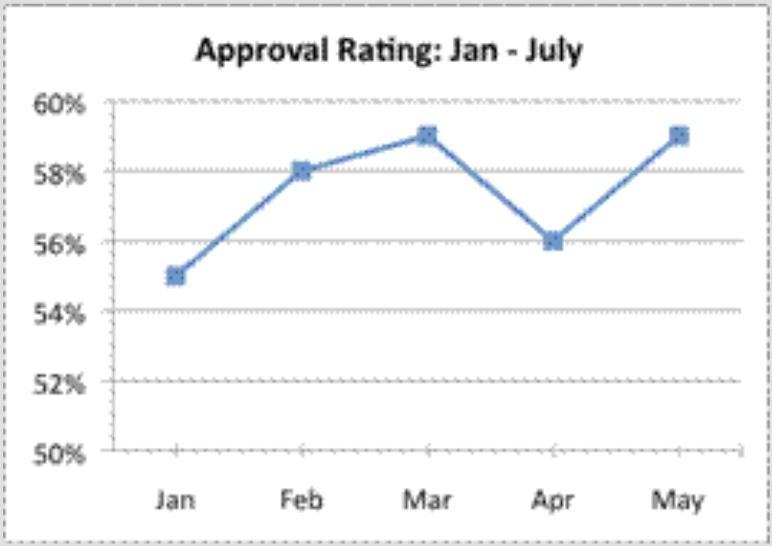
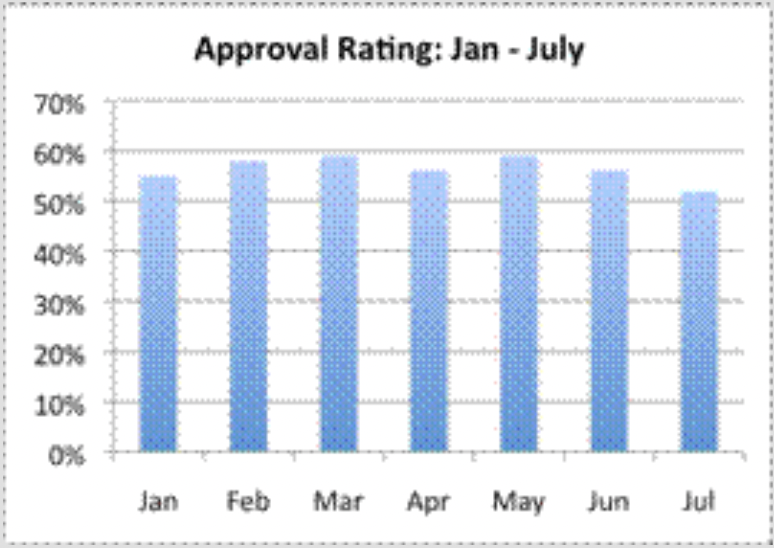
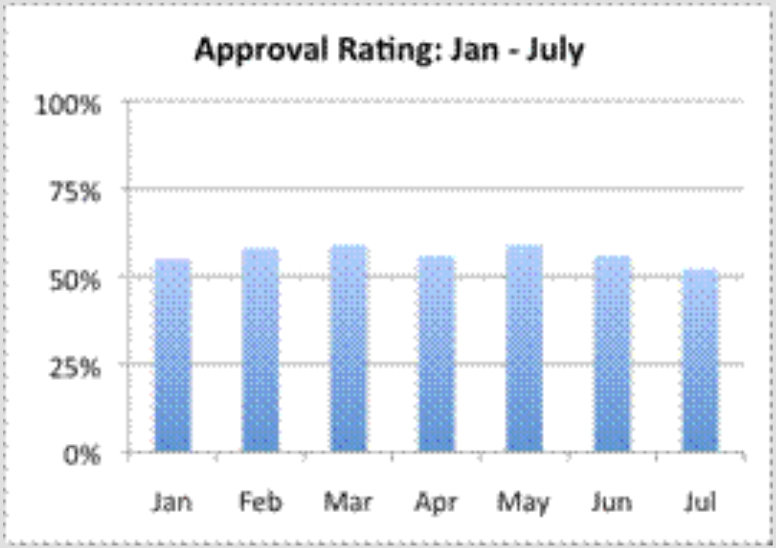
¿Cuál de las siguientes gráficas es más engañosa?
- Responder
-
- Incorrecto.
Este gráfico de líneas muestra con precisión los datos; los ejes están etiquetados apropiadamente, y la escala es de 0% a 100%. El gráfico muestra que aunque ha habido alguna variación hacia arriba y hacia abajo, el índice de aprobación del político se ha mantenido a mediados de los 50's La respuesta correcta es Gráfica B.
- Correcto.
Esta gráfica utiliza una escala muy pequeña (10%, de 50% a 60%) y ha eliminado los dos puntos finales de datos. Esta gráfica representa sólo una parte de los datos, y está diseñada para que el lector piense que el político está calificado de manera más favorable de lo que realmente es.
- Incorrecto.
Este gráfico de barras muestra con precisión los datos; los ejes están etiquetados apropiadamente y la escala es de 0% a 70%. Las calificaciones de aprobación del político se ven un poco más altas en esta gráfica que en la Gráfica D, pero no hay nada deshonesto en esta gráfica. El gráfico muestra que aunque ha habido alguna variación hacia arriba y hacia abajo, el índice de aprobación del político se ha mantenido a mediados de los 50's La respuesta correcta es Gráfica B.
- Incorrecto.
Este gráfico de barras muestra con precisión los datos; los ejes están etiquetados apropiadamente, y la escala es de 0% a 100%, con incrementos de 25%. Se ve diferente a la Gráfica C, pero los datos en sí no son engañosos: es la escala de los datos lo que es diferente. La respuesta correcta es Gráfica B.
- Incorrecto.
Resumen
Los gráficos tienen un gran impacto en la forma de entender un conjunto de datos. Usa un tipo de gráfico apropiado y podrás comunicar tus datos de manera efectiva; sin embargo, usa el tipo de gráfico incorrecto y tus espectadores pueden malinterpretar la historia que intentas contar. Al leer gráficos en periódicos y en línea, asegúrese de mirar los ejes, la escala y la presentación de los datos en sí. Todos estos pueden ayudarte a identificar si el gráfico representa un conjunto de datos de manera justa o injusta.