9.1.2: Enteros

Última actualización
Guardar como PDF

Page ID: 111308

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Localice números enteros en una recta numérica.
Encuentra el valor absoluto de un número dado.
Encuentra lo contrario de un número dado.

Introducción

Has trabajado con números en una línea numérica. Ya sabes graficar números como 0, 1, 2, 3, etc. en la recta numérica. Hay otros tipos de números que también se pueden graficar en la recta numérica. Veamos cómo se ven y dónde se encuentran en la recta numérica.

Números Naturales y Números Enteros

En matemáticas, a veces es útil hablar de grupos de cosas, que se llaman conjuntos. Los números se pueden agrupar en conjuntos, y un número particular puede pertenecer a más de un conjunto.

Probablemente estés familiarizado con el conjunto de números naturales, que también se llaman los números de conteo. Estos son los números 1, 2, 3, y así sucesivamente, los números que usamos al contar.

La siguiente ilustración muestra los números naturales graficados en una recta numérica.

$Screen Shot 2021-05-20 en 1.31.59 PM.png$

La recta numérica continúa en ambas direcciones. El conjunto de números naturales solo continúa hacia la derecha, por lo que puede incluir 6, 7, y así sucesivamente, hasta cientos, miles y más allá. ¡Solo puedes mostrar tanto en una foto!

Cuando se agrega 0 al conjunto de 1, 2, 3, y así sucesivamente, forma el conjunto de números enteros. Estos se llaman “enteros” porque no tienen partes fraccionarias. (Un truco para ayudarte a recordar cuáles son números naturales y cuáles son números enteros es pensar en un “agujero”, que puede ser representado por 0. Los números enteros (“agujero”) incluyen 0, los números naturales no.)

La siguiente ilustración muestra los números enteros representados en la recta numérica.

$Screen Shot 2021-05-20 en 1.36.38 PM.png$

Enteros

Cuando trabajas con algo así como la temperatura, a veces quieres usar números que son menores a cero, que se llaman números negativos. Los números negativos se escriben usando un signo negativo al frente, como -1, -5 y -30. Estos se leen negativo uno, negativo cinco y negativo treinta. (El signo negativo no debe leerse como menos; menos significa resta.)

Los números mayores que 0 se denominan números positivos y se pueden escribir con o sin el signo “+”. ¡Observe que 0 no es ni positivo ni negativo!

Los enteros son los números:..., -3, -2, -1, 0, 1, 2, 3,... Observe que todos los números enteros también son enteros. La siguiente ilustración muestra los enteros graficados en la recta numérica. Los enteros incluyen cero y continúan a la derecha y a la izquierda.

$Screen Shot 2021-05-20 en 1.44.46 PM.png$

Ejercicio

El número 0 pertenece a cuál de los siguientes conjuntos de números?

números naturales

números enteros

enteros

solo números naturales
solo números enteros
números naturales y enteros
solo enteros
números enteros y enteros

Contestar

Incorrecto. Los números naturales son 1, 2, 3, y así sucesivamente. No incluyen 0. La respuesta correcta son números enteros y enteros.
Incorrecto. Mientras que los números enteros incluyen 0, también lo hacen los enteros. La respuesta correcta son números enteros y enteros.
Incorrecto. Los números naturales son 1, 2, 3, y así sucesivamente. No incluyen 0. La respuesta correcta son números enteros y enteros.
Incorrecto. Mientras que los números enteros incluyen 0, también lo hacen los números enteros. La respuesta correcta son números enteros y enteros.
Correcto. Tanto los números enteros como los enteros incluyen 0, pero los números naturales no.

Valor absoluto y la línea numérica

La línea numérica a continuación muestra todos los números enteros entre e incluyendo -5 y 5. Observe que los enteros positivos van a la derecha: 1, 2, 3, y así sucesivamente. Los enteros negativos van a la izquierda: -1, -2, -3, y así sucesivamente.

$Screen Shot 2021-05-20 en 1.51.15 PM.png$

La distancia entre el lugar de un número en la línea numérica y 0 se denomina valor absoluto del número. Para escribir el valor absoluto de un número, utilice líneas verticales cortas (|) a cada lado del número. Por ejemplo, el valor absoluto de -3 se escribe como barra negativa tres barras.

Observe que la distancia siempre es positiva o 0.

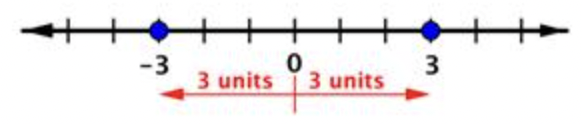
|-3| = 3, ya que -3 está a 3 unidades de distancia de 0 y |3|=3, ya que 3 está a 3 unidades de distancia de 0.

$Screen Shot 2021-05-20 at 1.56.58 PM.png$

Aquí hay algunos otros ejemplos.

\ (\\ begin {array} {c}
|0|=0\\
|-23|=23\\
|6|=6\\
|817|=817\\
|-3.000|=3.000
\ end {array}\)

Ejemplo

Encuentra$\ |x|$ cuándo$\ x=-7$.

Solución

$\ |x|$

$\ |-7|$

Sustituir -7 por$\ x$ en la expresión.

$\ |-7|=7$

Dado que -7 es 7 unidades a partir de 0, el valor absoluto es 7.

Para ubicar un entero en la recta numérica, imagínese parado en la recta numérica en 0. Si el número es 0, estás ahí. Si el número es positivo, de cara a la derecha hacia números mayores que 0. Si el número es negativo, boca a la izquierda hacia números menores a 0. Después, avanzar el número de unidades igual al valor absoluto del número.

Ejemplo

Encuentra -4 en la línea numérica. Después determinar |-4|.

Solución

$Screen Shot 2021-05-20 a las 2.13.32 PM.png$

Imagínese de pie en 0. Ya que -4 es negativo, de cara a la izquierda.

Mueve 4 unidades de 0 en la dirección negativa.

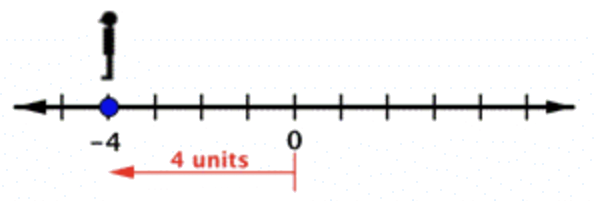$Screen Shot 2021-05-20 a las 2.17.19 PM.png$

Dibuja un punto en la recta numérica en esa ubicación, que es -4.

$\ |-4|=4$

La dirección movida no afecta al valor absoluto, solo a la distancia movida.

Ejercicio

¿Qué punto representa -2 en esta recta numérica?

$Screen Shot 2021-05-20 a las 2.28.36 PM.png$

Contestar

Incorrecto. Este punto está 4 unidades a la izquierda de 0, por lo que representa -4. El punto que representa -2 está a 2 unidades a la izquierda de 0. El punto B es correcto.
Correcto. El punto B está a 2 unidades a la izquierda de 0, por lo que representa -2.
Incorrecto. Este punto está 1 unidad a la izquierda de 0, por lo que representa -1. El punto que representa -2 está a 2 unidades a la izquierda de 0. El punto B es correcto.
Incorrecto. Este punto es 1 unidad a la derecha de 0, por lo que representa 1. Un número negativo debe estar a la izquierda de 0. El punto que representa -2 está a 2 unidades a la izquierda de 0. El punto B es correcto.
Incorrecto. Este punto se encuentra a 2 unidades a la derecha de 0. Un número negativo debe estar a la izquierda de 0. El punto que representa -2 está a 2 unidades a la izquierda de 0. El punto B es correcto.

Opuestos

Habrás notado que, a excepción de 0, los enteros vienen en pares de números positivos y negativos: 1 y -1, 3 y -3, 72 y -3, 72 y -72, y así sucesivamente. Cada número es el opuesto del otro número en el par: 72 es el opuesto de -72, y -72 es el opuesto de 72.

Un número y su opuesto están a la misma distancia de 0, por lo que tienen el mismo valor absoluto.

$\ |72|=72, \text { and }|-72|=72$

El conjunto de enteros son todos los números enteros y sus opuestos.

Ejercicio

¿Qué es lo contrario de -29?

Contestar: Lo contrario de -29 es 29.

Resumen

Algunos números son números naturales (1, 2, 3,...) o números enteros (0, 1, 2, 3,...). Los números enteros también son enteros. Hay otros enteros que son los opuestos de los números enteros (-1, -2, -3,...). Estos números negativos se encuentran a la izquierda de 0 en la recta numérica. Los enteros son los números enteros y sus opuestos. El valor absoluto de un número es su distancia a 0 en la recta numérica. Los valores absolutos son siempre positivos o 0.