9.1.3: Números racionales y reales
- Page ID
- 111309
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identificar el/los subconjunto (s) de los números reales a los que pertenece un número dado.
- Localizar puntos en una recta numérica.
- Comparar números racionales.
- Identificar números racionales e irracionales.
Introducción
Has trabajado con fracciones y decimales, como 3.8 y\(\ 21 \frac{2}{3}\). Estos números se pueden encontrar entre los números enteros en una recta numérica. Hay otros números que también se pueden encontrar en una recta numérica. Cuando incluyes todos los números que se pueden poner en una recta numérica, tienes la línea numérica real. Profundicemos en la recta numérica para ver cómo se ven esos números y dónde caen en la recta numérica.
Números racionales
La fracción\(\ \frac{16}{3}\), número mixto\(\ 5 \frac{1}{3}\), y decimal 5.33... (o\(\ 5 . \overline{3}\)) todos representan el mismo número. Este número pertenece a un conjunto de números que los matemáticos llaman números racionales. Los números racionales son números que se pueden escribir como una proporción de dos enteros. Independientemente de la forma utilizada,\(\ 5 . \overline{3}\) es racional porque este número se puede escribir como la proporción de 16 sobre 3, o\(\ \frac{16}{3}\).
Ejemplos de números racionales incluyen los siguientes.
0.5, ya que puede escribirse como\(\ \frac{1}{2}\)
\(\ 2 \frac{3}{4}\), ya que puede escribirse como\(\ \frac{11}{4}\)
\(\ -1.6\), ya que puede escribirse como\(\ -1 \frac{6}{10}=\frac{-16}{10}\)
\(\ 4\), ya que puede escribirse como\(\ \frac{4}{1}\)
-10, ya que puede escribirse como\(\ \frac{-10}{1}\)
Todos estos números se pueden escribir como la relación de dos enteros.
Puedes ubicar estos puntos en la recta numérica.
En la siguiente ilustración, se muestran puntos para 0.5 o\(\ \frac{1}{2}\), y para 2.75 o\(\ 2 \frac{3}{4}=\frac{11}{4}\).
Como has visto, los números racionales pueden ser negativos. Cada número racional positivo tiene un opuesto. Lo contrario de\(\ 5 . \overline{3}\) es\(\ -5 . \overline{3}\), por ejemplo.
Tenga cuidado al colocar números negativos en una recta numérica. El signo negativo significa que el número está a la izquierda de 0, y el valor absoluto del número es la distancia desde 0. Entonces, para colocar -1.6 en una recta numérica, encontrarías un punto que es |-1.6| o 1.6 unidades a la izquierda de 0. Esto está a más de 1 unidad de distancia, pero a menos de 2.
Colocar\(\ -\frac{23}{5}\) en una línea numérica.
Solución
Es útil escribir primero esta fracción impropia como un número mixto: 23 dividido por 5 es 4 con el resto de 3, así\(\ -\frac{23}{5}\) es\(\ -4 \frac{3}{5}\).
Dado que el número es negativo, se puede pensar en él como\(\ 4 \frac{3}{5}\) unidades móviles a la izquierda de 0. \(\ -4 \frac{3}{5}\)estará entre -4 y -5.
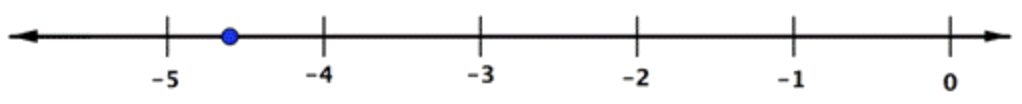
¿Cuál de los siguientes puntos representa\(\ -1 \frac{1}{4}\)?
- Responder
-
- Incorrecto. Este punto está poco más de 2 unidades a la izquierda de 0. El punto debe estar 1.25 unidades a la izquierda de 0. La respuesta correcta es el punto B.
- Correcto. Los números negativos están a la izquierda de 0, y\(\ -1 \frac{1}{4}\) deben estar 1.25 unidades a la izquierda. El punto B es el único punto que tiene más de 1 unidad y menos de 2 unidades a la izquierda de 0.
- Incorrecto. Observe que este punto está entre 0 y y la primera marca de unidad a la izquierda de 0, por lo que representa un número entre -1 y 0. El punto para\(\ -1 \frac{1}{4}\) debe ser 1.25 unidades a la izquierda de 0. Es posible que hayas encontrado correctamente 1 unidad a la izquierda, pero en lugar de continuar hacia la izquierda otra 0.25 unidad, te moviste a la derecha. La respuesta correcta es el punto B.
- Incorrecto. Los números negativos están a la izquierda de 0, no a la derecha. El punto para\(\ -1 \frac{1}{4}\) debe ser 1.25 unidades a la izquierda de 0. La respuesta correcta es el punto B.
- Incorrecto. Este punto está 1.25 unidades a la derecha de 0, por lo que tiene la distancia correcta pero en la dirección equivocada. Los números negativos están a la izquierda de 0. La respuesta correcta es el punto B.
Comparando números racionales
Cuando se grafican dos números enteros en una recta numérica, el número a la derecha en la recta numérica siempre es mayor que el número de la izquierda.
Lo mismo ocurre cuando se comparan dos enteros o números racionales. El número a la derecha en la recta numérica siempre es mayor que el de la izquierda.
Aquí hay algunos ejemplos.
| Números para comparar | Comparación | Expresión Simbólica |
| \(\ -2 \text { and }-3\) | -2 es mayor que -3 porque -2 está a la derecha de -3 | \(\ -2>-3 \text { or }-3<-2\) |
| \(\ 2 \text { and } 3\) | 3 es mayor que 2 porque 3 está a la derecha de 2 | \(\ 3>2 \text { or } 2<3\) |
| \(\ -3.5 \text { and }-3.1\) | -3.1 es mayor que -3.5 porque -3.1 está a la derecha de -3.5 (ver abajo) | \ (\\ begin {array} {l} -3.1>-3.5\ text {or} -3.5<-3.1 \ end {array}\) |
¿Cuáles de las siguientes son ciertas?
Opción\(\ \text { 1. }-4.1>3.2\)
Opción\(\ \text { 2. }-3.2>-4.1\)
Opción\(\ \text { 3. }3 .2>4.1\)
Opción\(\ \text { 4. }-4.6<-4.1\)
- Opción 1 y Opción 4
- Opción 1 y Opción 2
- Opción 2 y Opción 3
- Opción 2 y Opción 4
- Opciones 1, 2 y 3
- Responder
-
- Incorrecto. -4.6 está a la izquierda de -4.1, entonces -4.6<-4.1. Sin embargo, los números positivos como 3.2 están siempre a la derecha de números negativos como -4.1, por lo que 3.2>-4.1 o -4.1<3.2. La respuesta correcta es ii y iv, -3.2>-4.1 y -4.6<-4.1.
- Incorrecto. -3.2 está a la derecha de -4.1, entonces -3.2>-4.1. Sin embargo, los números positivos como 3.2 están siempre a la derecha de números negativos como -4.1, por lo que 3.2>-4.1 o -4.1<3.2. La respuesta correcta es ii y iv, -3.2>-4.1 y -4.6<-4.1.
- Incorrecto. -3.2 está a la derecha de -4.1, entonces -3.2>-4.1. Sin embargo, 3.2 está a la izquierda de 4.1, por lo que 3.2<4.1. La respuesta correcta es ii y iv, -3.2>-4.1 y -4.6<-4.1.
- Correcto. -3.2 está a la derecha de -4.1, entonces -3.2>-4.1. Además, -4.6 está a la izquierda de -4.1, por lo que -4.6<-4.1.
- Incorrecto. -3.2 está a la derecha de -4.1, entonces -3.2>-4.1. Sin embargo, los números positivos como 3.2 están siempre a la derecha de números negativos como -4.1, por lo que 3.2>-4.1 o -4.1<3.2. Además, 3.2 está a la izquierda de 4.1, por lo que 3.2<4.1. La respuesta correcta es ii y iv, -3.2>-4.1 y -4.6<-4.1.
Números irracionales y reales
También hay números que no son racionales. Los números irracionales no pueden escribirse como la relación de dos enteros.
Cualquier raíz cuadrada de un número que no sea un cuadrado perfecto, por ejemplo\(\ \sqrt{2}\), es irracional. Los números irracionales se escriben más comúnmente de una de tres maneras: como una raíz (como una raíz cuadrada), usando un símbolo especial (como\(\ \pi\)), o como un decimal no repetitivo y no terminante.
Los números con una parte decimal pueden ser decimales de terminación o decimales no terminantes. Terminación significa que los dígitos se detienen eventualmente (aunque siempre puedes escribir ceros al final). Por ejemplo, 1.3 está terminando, porque hay un último dígito. La forma decimal de\(\ \frac{1}{4}\) es 0.25. Los decimales de terminación son siempre racionales.
Los decimales no terminales tienen dígitos (distintos a 0) que continúan para siempre. Por ejemplo, considere la forma decimal de\(\ \frac{1}{3}\), que es 0.3333... Los 3s continúan indefinidamente. O la forma decimal de\(\ \frac{1}{11}\), que es 0.090909...: la secuencia “09" continúa para siempre.
Además de ser no terminadores, estos dos números también están repitiendo decimales. Sus partes decimales están hechas de un número o secuencia de números que se repite una y otra vez. Un decimal no repetido tiene dígitos que nunca forman un patrón repetitivo. El valor de\(\ \sqrt{2}\), por ejemplo, es de 1.414213562... No importa lo lejos que lleves a cabo los números, los dígitos nunca repetirán una secuencia anterior.
Si un número está terminando o repitiendo, debe ser racional; si es tanto no terminante como no repetitivo, el número es irracional.
| Tipo de Decimal | Racional o irracional | Ejemplos |
| Terminando | Racional |
\(\ \left.0.25 \text { (or } \frac{1}{4}\right)\) \(\ \left.1.3 \text { (or } \frac{13}{10}\right)\) |
| No terminante y repetitivo | Racional |
\(\ \left.0.66 \ldots \text { (or } \frac{2}{3}\right)\) \(\ 3.242424 \ldots \text { (or) }\) \(\ \frac{321}{99}=\frac{107}{33}\) |
| No terminante y no repetitivo | Irracional |
\(\ \pi \text { (or 3.14159...) }\) \(\ \sqrt{7} \text { (or } 2.6457 \ldots)\) |
¿El -82.91 es racional o irracional?
Solución
| -82.91 es racional. | El número es racional, porque es un decimal de terminación. |
El conjunto de números reales se realiza combinando el conjunto de números racionales y el conjunto de números irracionales. Los números reales incluyen números naturales o números de conteo, números enteros, números enteros, números racionales (fracciones y decimales repetitivos o de terminación) y números irracionales. El conjunto de números reales son todos los números que tienen una ubicación en la línea numérica.
Números naturales 1, 2, 3,...
Números enteros 0, 1, 2, 3,...
Enteros..., -3, -2, -1, 0, 1, 2, 3,...
Números racionales: números que se pueden escribir como una proporción de dos enteros: los números racionales terminan o se repiten cuando se escriben en forma decimal
Números irracionales: números que no se pueden escribir como una proporción de dos enteros: los números irracionales no terminan y no se repiten cuando se escriben en forma decimal
Números reales: cualquier número que sea racional o irracional
¿A qué conjuntos de números pertenece 32?
Solución
| El número 32 pertenece a todos estos conjuntos de números:
Números naturales Números enteros Enteros Números racionales Números reales |
¡Cada número natural o de conteo pertenece a todos estos conjuntos! |
¿A qué conjuntos de números\(\ 382 . \overline{3}\) pertenece?
Solución
| \(\ 382 . \overline{3}\)pertenece a estos conjuntos de números:
Números racionales Números reales |
El número es racional porque es un decimal repetido. Es igual a\(\ 382 \frac{1}{3}\) o\(\ \frac{1,147}{3}\), o\(\ 382 . \overline{3}\). |
¿A qué conjuntos de números\(\ -\sqrt{5}\) pertenece?
Solución
| \(\ -\sqrt{5}\)pertenece a estos conjuntos de números:
Números irracionales Números reales |
El número es irracional porque no se puede escribir como una relación de dos enteros. Las raíces cuadradas que no son cuadrados perfectos son siempre irracionales. |
¿A cuál de los siguientes conjuntos\(\ \frac{-33}{5}\) pertenece?
números enteros
enteros
números racionales
números irracionales
números reales
- solo números racionales
- números irracionales solamente
- números racionales y reales
- números irracionales y reales
- números enteros, números racionales y números reales
- números enteros, números racionales y números reales
- Responder
-
- Incorrecto. El número es racional (está escrito como una proporción de dos enteros) pero también es real. Todos los números racionales son también números reales. La respuesta correcta son los números racionales y reales, porque todos los números racionales también son reales.
- Incorrecto. Los números irracionales no se pueden escribir como una relación de dos enteros. La respuesta correcta son los números racionales y reales, porque todos los números racionales también son reales.
- Correcto. El número está entre enteros, por lo que no puede ser un número entero o un número entero. Está escrito como una proporción de dos enteros, entonces es un número racional y no irracional. Todos los números racionales son números reales, por lo que este número es racional y real.
- Incorrecto. Los números irracionales no se pueden escribir como una relación de dos enteros. La respuesta correcta son los números racionales y reales, porque todos los números racionales también son reales.
- Incorrecto. El número está entre enteros, no un entero en sí mismo. La respuesta correcta son los números racionales y reales.
- Incorrecto. El número está entre enteros, por lo que no puede ser un número entero o un número entero. La respuesta correcta son los números racionales y reales.
Resumen
El conjunto de números reales son todos los números que se pueden mostrar en una línea numérica. Esto incluye números naturales o de conteo, números enteros y números enteros. También incluye números racionales, que son números que pueden escribirse como una relación de dos enteros, y números irracionales, que no pueden escribirse como una relación de dos enteros. Al comparar dos números, el de mayor valor aparecería en la recta numérica a la derecha del que tiene el menor valor.