11.2.4: Multiplicar casos especiales

Última actualización
Guardar como PDF

Page ID: 111469

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Cuadrando un binomio.
Multiplicar la suma y diferencia de los mismos dos términos.

Introducción

Si bien la propiedad distributiva se puede usar para toda la multiplicación polinómica, algunos productos con binomios se pueden encontrar usando atajos. Estos métodos a veces se llaman productos especiales.

Cuadrado de una suma binomial

Multiplicar un número por sí mismo a menudo se llama cuadratura. Se puede representar esta multiplicación como un cuadrado. El número al cuadrado es la longitud de los lados del cuadrado y el producto está representado por el área de ese cuadrado. Considera un cuadrado cuya longitud lateral es descrita por el binomio$\ x+3$:

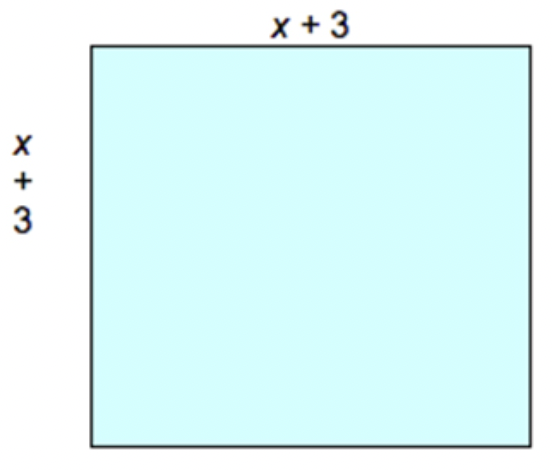
$Screen Shot 2021-06-14 a las 2.16.54 PM.png$

El área de esta plaza es$\ (x+3)(x+3) \text { or }(x+3)^{2}$.

A continuación se muestra el mismo cuadrado, pero se separan los términos variables y constantes:

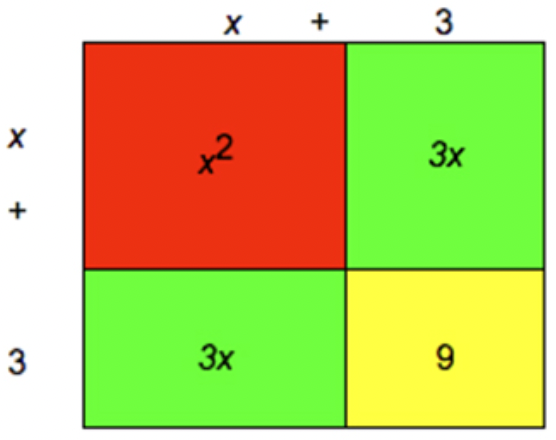
$Screen Shot 2021-06-14 a las 2.25.34 PM.png$

A partir de este modelo de área, se puede ver que el área puede ser descrita por la suma de las piezas rojas, verdes y amarillas. Es decir, la zona es$\ x^{2}+3 x+3 x+9=x^{2}+6 x+9$.

Entonces$\ (x+3)^{2}=x^{2}+3 x+3 x+9=x^{2}+6 x+9$.

También puedes encontrar el cuadrado de una suma de dos términos usando el método FOIL.

Ejemplo

Cuadrando el binomio. $\ (x+5)^{2}$.

Solución

$\ (x+5)(x+5)$	Multiplicar el binomio por sí mismo.
\ (\\ comenzar {alineado} \ texto {Primero:} x\ cdot x &=x^ {2}\\ \ texto {Exterior:} x\ cdot 5 &=5 x\ \\ texto {Interior:} 5\ cdot x &=5 x\ \ texto {Último:} 5\ cdot 5 &=25 \ fin {alineado}\)
$\ x^{2}+5 x+5 x+25$	Agregar los términos.
$\ x^{2}+10 x+25$	Combina términos similares.

$\ (x+5)^{2}=x^{2}+10 x+25$

Observe que los términos Exterior e Interior son los mismos.

Hasta ahora, tenemos dos ejemplos de cuadrar una suma de dos términos, uno a partir de la construcción de un modelo de área y otro a partir de cálculos algebraicos:

\ (\\ begin {array} {l}
(x+3) ^ {2} =x^ {2} +6 x+9\\
(x+5) ^ {2} =x^ {2} +10 x+25
\ end {array}\)

En ambos casos, el primer término se cuadra para obtener el primer término del producto. Los dos términos se multiplican y duplican para el término medio del producto, y el último término se cuadra para el último término del producto.

Este patrón se mantendrá cierto para el cuadrado de la suma de dos términos cualesquiera: Cuadrar el primer término, agregar dos veces el producto del primer y el último término, agregar el último término al cuadrado.

Al cuadrado de una suma binomial

Para cuadrar un binomio, haga lo siguiente:

Cuadrado el primer término.
Agregar el producto de los dos términos medios, veces dos.
Agregar el cuadrado del último término.

Este proceso se ilustra con el siguiente caso:

$\ (a+b)^{2}=a^{2}+2 a b+b^{2}$

Ejemplo

Cuadrando el binomio. $\ (2 x+6)^{2}$

Solución

$\ (2 x)^{2}=4 x^{2}$	Cuadrado el primer término.
$\ (2 x)(6)(2)=24 x$	Multiplique los dos términos juntos y duplique el producto.
$\ 6^{2}=36$	Cuadrarse el último término.
$\ 4 x^{2}+24 x+36$	Combina los términos.

$\ (2 x+6)^{2}=4 x^{2}+24 x+36$

Puedes verificar esta respuesta usando la propiedad distributiva o FOIL.

Ejercicio

Encuentra el producto:$\ (2 s+9)^{2}$

$\ 4 s^{2}+81$
$\ 4 s+18$
$\ 4 s^{2}+36 s+81$
$\ 4 s^{2}+18 s+18$

Contestar

Incorrecto. Usted cuadró el primer término, y cuadró el último término. Pero olvidaste el término medio, que es 2 veces el producto de 2s y 9, que es 36s. La respuesta correcta es$\ 4 s^{2}+36 s+81$.
Incorrecto. Debes cuadrar$\ (2 s+9)$, no duplicarlo. $\ (a+b)^{2}=a^{2}+2 a b+b^{2}$; en este ejemplo,$\ a=2 s$ y$\ b=9$, así$\ (2 s+9)^{2}=4 s^{2}+36 s+81$.
Correcto. $\ (a+b)^{2}=a^{2}+2 a b+b^{2}$; en este ejemplo,$\ a=2 s$ y$\ b=9$ así$\ (2 s+9)^{2}=4 s^{2}+2(18 s)+81=4 s^{2}+36 s+81$.
Incorrecto. Los términos$\ 18 s$ y 18 son incorrectos. $\ (a+b)^{2}=a^{2}+2 a b+b^{2}$; en este ejemplo,$\ a=2 s$ y$\ b=9$, así$\ (2 s+9)^{2}=4 s^{2}+36 s+81$.

Cuadrado de una diferencia binomial

¿También hay un patrón cuando cuadras la diferencia entre dos términos? ¡Sí! Dado que la resta se puede expresar como sumar lo contrario, se produce un patrón similar.

Considera el cuadrado del binomio$\ (x-7)$. Puedes usar FOIL.

Ejemplo

Cuadrando el binomio. $\ (x-7)^{2}$

Solución

$\ (x-7)(x-7)$	Reescribir como multiplicación.
\ (\\ begin {array} {c} \ text {Primero:} x\ cdot x=x^ {2}\ \\ text {Exterior:} x\ cdot-7=-7 x\ \ texto {Interior:} -7\ cdot x=-7 x\ \ texto {Último:} -7\ cdot-7=49 \ end {array}\)
$\ x^{2}+(-7 x)+(-7 x)+49$	Agregar los términos.
$\ x^{2}-14 x+49$	Combina los términos similares.

$\ (x-7)^{2}=x^{2}-14 x+49$

Observe que el patrón es similar al cuadrar la suma de un binomio.

Cuadrando una Diferencia Binomial

Para cuadrar una diferencia binomial, haga lo siguiente:

Cuadrado el primer término
Restar el producto de los dos términos medios, por dos
Agregar el cuadrado del último término.

$\ (a-b)^{2}=a^{2}-2 a b+b^{2}$

Ejemplo

Cuadrar el binomio. $\ (4 s-3)^{2}$

Solución

$\ (4 s)^{2}=16 s^{2}$	Cuadrar el primer término, incluyendo el coeficiente.
$\ (4 s)(-3)(2)=-24 s$	Multiplique los dos términos juntos y duplique el producto.
$\ (-3)^{2}=9$	Cuadrarse el último término.
$\ 16 s^{2}-24 s+9$	Agregar los términos.

$\ (4 s-3)^{2}=16 s^{2}-24 s+9$

Ejercicio

Cuadrando el binomio. $\ (2 r-9)^{2}$

$\ 4 r^{2}-81$
$\ 4 r-18$
$\ 4 r^{2}-36 r+81$
$\ 4 r^{2}+18 r-18$

Contestar

Incorrecto. Cuadraste el primer término correctamente, y cuadraste el último término correctamente, pero olvidaste que hay un término medio, que es$\ (2 r)(-9)(2)=-36 r$. La respuesta correcta es$\ 4 r^{2}-36 r+81$.
Incorrecto. El exponente 2 significa que el binomio debe ser cuadrado, no duplicado. La respuesta correcta es$\ 4 r^{2}-36 r+81$.
Correcto. $\ (a-b)^{2}=a^{2}-2 a b+b^{2}$, y en este caso$\ a=2 r$ y$\ b=9$. Entonces$\ (2 r-9)^{2}=4 r^{2}-36 r+81$.
Incorrecto. Los términos$\ 18 r$ y -18 son incorrectos. $\ (a-b)^{2}=a^{2}-2 a b+b^{2}$, y en este caso$\ a=2 r$ y$\ b=9$. Entonces$\ (2 r-9)^{2}=4 r^{2}-36 r+81$.

Producto de una suma y una diferencia

Hay un tercer producto especial a considerar entre binomios: el producto de la suma de dos términos y la diferencia de los mismos dos términos. En este caso, también hay un patrón. Aquí hay un ejemplo:

Ejemplo

Multiplicar los binomios. $\ (x+8)(x-8)$

Solución

\ (\\ begin {array} {r} \ text {Primero:} x\ cdot x=x^ {2}\ \\ texto {Exterior:} x\ cdot-8=-8 x\ \ texto {Interior:} 8\ cdot x=+8 x\ \ texto {Último:} 8\ cdot-8=-64 \ end {array}\)
$\ x^{2}-8 x+8 x-64$	Agregar los términos.

$\ (x+8)(x-8)=x^{2}-64$

Tenga en cuenta que la respuesta a este producto binomial es un binomio en sí mismo: la diferencia de dos cuadrados perfectos. No hay término medio en este caso. ¿Por qué sucede esto? Los dos términos son opuestos y por lo tanto se suman a cero.

Producto de una suma y una diferencia

El producto de la suma de dos términos$\ (a+b)$ y la diferencia de los mismos términos$\ (a-b)$ es la diferencia de los cuadrados de los dos términos.

$\ (a+b)(a-b)=(a-b)(a+b)=a^{2}-b^{2}$

Ejemplo

Multiplicar los binomios. $\ (2 n-5)(2 n+5)$

Solución

$\ (2 n)^{2}=4 n^{2}$	Cuadrar el primer término, incluyendo el coeficiente.
$\ (5)^{2}=25$	Cuadrarse el último término.
$\ 4 n^{2}-25$	Toma la diferencia.

$\ (2 n-5)(2 n+5)=4 n^{2}-25$

Ejercicio

Encuentra el producto:$\ (2 r-9)(2 r+9)$

$\ 4 r^{2}-81$
$\ 4 r-18$
$\ 4 r^{2}-36 r+81$
$\ 4 r^{2}-36 r-81$

Contestar

Correcto. $\ (a-b)(a+b)=a^{2}-b^{2}$, y en este caso$\ a=2 r$ y$\ b=9$. Entonces$\ (2 r-9)(2 r+9)=4 r^{2}-81$.
Incorrecto. Cada término debe ser cuadrado, no duplicado. $\ (2 r-9)(2 r+9)=4 r^{2}-81$.
Incorrecto. Este no es el cuadrado de una diferencia. Un binomio es una diferencia pero el otro es una suma. $\ (a-b)(a+b)=a^{2}-b^{2}$, y en este caso$\ a=2 r$ y$\ b=9$. Entonces$\ (2 r-9)(2 r+9)=4 r^{2}-81$.
Incorrecto. $\ (a-b)(a+b)=a^{2}-b^{2}$, y en este caso$\ a=2 r$ y$\ b=9$. Entonces$\ (2 r-9)(2 r+9)=4 r^{2}-81$.

Resumen

Algunos productos de multiplicar binomios siguen un patrón predecible que facilita su multiplicación. Estos son conocidos como productos especiales. Hay tres productos especiales de binomios que cada uno sigue una fórmula específica: cuadrar la suma de un binomio, cuadrar la diferencia de un binomio y el producto de una suma y una diferencia.

\(\ (x+5)(x+5)\)	Multiplicar el binomio por sí mismo.
\ (\\ comenzar {alineado} \ texto {Primero:} x\ cdot x &=x^ {2}\\ \ texto {Exterior:} x\ cdot 5 &=5 x\ \\ texto {Interior:} 5\ cdot x &=5 x\ \ texto {Último:} 5\ cdot 5 &=25 \ fin {alineado}\)
\(\ x^{2}+5 x+5 x+25\)	Agregar los términos.
\(\ x^{2}+10 x+25\)	Combina términos similares.

\(\ (2 x)^{2}=4 x^{2}\)	Cuadrado el primer término.
\(\ (2 x)(6)(2)=24 x\)	Multiplique los dos términos juntos y duplique el producto.
\(\ 6^{2}=36\)	Cuadrarse el último término.
\(\ 4 x^{2}+24 x+36\)	Combina los términos.

\(\ (x-7)(x-7)\)	Reescribir como multiplicación.
\ (\\ begin {array} {c} \ text {Primero:} x\ cdot x=x^ {2}\ \\ text {Exterior:} x\ cdot-7=-7 x\ \ texto {Interior:} -7\ cdot x=-7 x\ \ texto {Último:} -7\ cdot-7=49 \ end {array}\)
\(\ x^{2}+(-7 x)+(-7 x)+49\)	Agregar los términos.
\(\ x^{2}-14 x+49\)	Combina los términos similares.

\(\ (4 s)^{2}=16 s^{2}\)	Cuadrar el primer término, incluyendo el coeficiente.
\(\ (4 s)(-3)(2)=-24 s\)	Multiplique los dos términos juntos y duplique el producto.
\(\ (-3)^{2}=9\)	Cuadrarse el último término.
\(\ 16 s^{2}-24 s+9\)	Agregar los términos.

\ (\\ begin {array} {r} \ text {Primero:} x\ cdot x=x^ {2}\ \\ texto {Exterior:} x\ cdot-8=-8 x\ \ texto {Interior:} 8\ cdot x=+8 x\ \ texto {Último:} 8\ cdot-8=-64 \ end {array}\)
\(\ x^{2}-8 x+8 x-64\)	Agregar los términos.

\(\ (2 n)^{2}=4 n^{2}\)	Cuadrar el primer término, incluyendo el coeficiente.
\(\ (5)^{2}=25\)	Cuadrarse el último término.
\(\ 4 n^{2}-25\)	Toma la diferencia.