11.2.3: Multiplicar polinomios
- Page ID
- 111465
- Multiplicar los monomios.
- Multiplicar monomios por polinomios.
- Multiplica dos binomios.
- Multiplica dos polinomios cualesquiera.
Introducción
Multiplicar polinomios implica aplicar las reglas de exponentes y la propiedad distributiva para simplificar el producto. Esta multiplicación también se puede ilustrar con un modelo de área, y puede ser útil para modelar situaciones del mundo real. Comprender los productos polinomiales es un paso importante para aprender a resolver ecuaciones algebraicas que involucran polinomios.
Multiplicar monomios
Empecemos multiplicando dos simples monomios juntos. Considera un rectángulo cuya longitud es\(\ 2x\) y cuyo ancho es\(\ 3x\). Para encontrar el área de este rectángulo, multiplica el largo por el ancho
\(\ \text { Area of rectangle }=(2 x)(3 x)=(2 x)(3 x)=2 \cdot 3 \cdot x \cdot x=6 x^{2}\)
Obsérvese que las propiedades conmutativas y asociativas de la multiplicación se utilizan para reorganizar los factores, juntando los coeficientes y las variables juntas.
El área,\(\ 6 x^{2}\), es un producto que incluye un coeficiente (6) y una variable con un exponente numérico entero (\(\ x^{2}\)). En otras palabras, también es un monomio. ¡Entonces el resultado de multiplicar dos monomios es otro monomio!
Probemos un problema un poco más complejo:\(\ -9 x^{3} \cdot 3 x^{2}\)
Multiplicar. \(\ -9 x^{3} \cdot 3 x^{2}\)
Solución
| \(\ -9 \cdot 3 \cdot x^{3} \cdot x^{2}\) | Utilice las propiedades conmutativas y asociativas de la multiplicación para reorganizar los factores. |
| \(\ -27 \cdot x^{3} \cdot x^{2}\) | Multiplicar constantes. Recuerde que un número positivo por un número negativo arroja un número negativo. |
| \ (\\ begin {array} {c} -27\ cdot x^ {3+2}\\ -27\ cdot x^ {5} \ end {array}\) |
Multiplicar términos variables. Recuerda sumar los exponentes al multiplicar exponentes con la misma base. |
\(\ -9 x^{3} \cdot 3 x^{2}=-27 x^{5}\)
¡Eso es! Al multiplicar los monomios, multiplique los coeficientes juntos, y luego multiplique las variables juntas. Si dos variables tienen la misma base, siga las reglas de los exponentes, así:
\(\ 5 a^{4} \cdot 7 a^{6}=35 a^{10}\)
Encuentra el área del rectángulo:
- \(\ 8 y^{3}\)
- \(\ 15 y^{5}\)
- \(\ 15 y^{10}\)
- \(\ 8 y^{5}\)
- Contestar
-
- Incorrecto. Multiplica los dos coeficientes para obtener 15, luego multiplica las variables. Usa las reglas de los exponentes:\(\ y^{3} \cdot y^{2}=y^{3+2}=y^{5}\). La respuesta correcta es\(\ 15 y^{5}\).
- Correcto. Multiplicar\(\ 3 \cdot 5\) y\(\ y^{3} \cdot y^{2}\), usando las reglas de exponentes para obtener\(\ 15 y^{5}\).
- Incorrecto. Cuando multiplicas con exponentes, si las bases son las mismas, agregas los exponentes:\(\ y^{3} \cdot y^{2}=y^{3+2}=y^{5}\). La respuesta correcta es\(\ 15 y^{5}\).
- Incorrecto. Usted multiplicó correctamente las variables\(\ y^{3} \cdot y^{2}=y^{3+2}=y^{5}\), pero parece que ha sumado los coeficientes en lugar de multiplicado. La respuesta correcta es\(\ 15 y^{5}\).
El Producto de un Monomio y un Polinomio
La propiedad distributiva se puede utilizar para multiplicar un polinomio por un monomio. Sólo recuerda que el monomio debe ser multiplicado por cada término en el polinomio. Considera la expresión\(\ 2 x\left(2 x^{2}+5 x+10\right)\).
Esta expresión se puede modelar con un boceto como el de abajo.
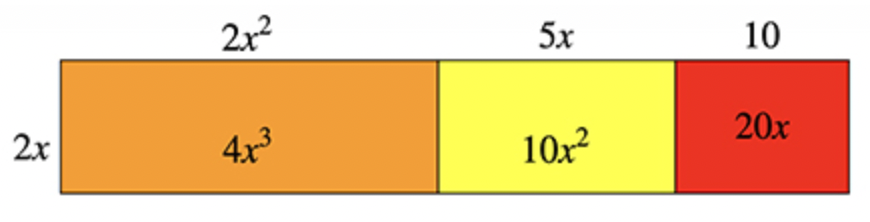
El modelo anterior ilustra la propiedad distributiva.
\(\ 2 x\left(2 x^{2}+5 x+10\right)=2 x \cdot 2 x^{2}+2 x \cdot 5 x=2 x \cdot 10=4 x^{3}+10 x^{2}+20 x\)
Aquí hay un ejemplo:
Simplificar. \(\ 5 x\left(4 x^{2}+3 x+7\right)\)
Solución
| \(\ 5 x \cdot 4 x^{2}+5 x \cdot 3 x+5 x \cdot 7\) | Distribuir el monomio a cada término del polinomio. |
| \(\ 20 x^{3}+15 x^{2}+35 x\) | Multiplicar. |
\(\ 5 x\left(4 x^{2}+3 x+7\right)=20 x^{3}+15 x^{2}+35 x\)
Es posible que deba reescribir la resta como agregar lo contrario.
Simplificar. \(\ 7 x^{2}\left(2 x^{2}-5 x+1\right)\)
Solución
| \(\ 7 x^{2}\left[2 x^{2}+(-5 x)+1\right]\) | Reescribe la resta como sumando lo contrario. |
| \(\ 7 x^{2} \cdot 2 x^{2}+7 x^{2} \cdot-5 x+7 x^{2} \cdot 1\) | Distribuir el monomio a cada término del polinomio. |
| \(\ 14 x^{4}+(-35) x^{3}+7 x^{2}\) | Multiplicar. |
| \(\ 7 x^{2}\left(2 x^{2}-5 x+1\right)=14 x^{4}-35 x^{3}+7 x^{2}\) | Reescribir la suma de términos con coeficientes negativos como resta. |
Encuentra el producto. ¡Vigila las señales!
\(\ -3 t^{2}\left(7 t^{3}+3 t^{2}-t\right)\)
- \(\ -21 t^{5}-9 t^{4}+3 t^{3}\)
- \(\ -21 t^{5}+9 t^{4}-3 t^{3}\)
- \(\ -21 t^{6}-9 t^{4}+3 t^{2}\)
- \(\ -21 t^{5}+3 t^{2}-t\)
- Contestar
-
- Correcto. Reescribir la resta como sumar lo contrario da\(\ -3 t^{2}\left[7 t^{3}+3 t^{2}+(-t)\right]\). Distribuyendo el monomio\(\ -3 t^{2}\) da\(\ -3 t^{2} \cdot 7 t^{3}+\left(-3 t^{2}\right) \cdot 3 t^{2}+\left(-3 t^{2}\right) \cdot(-t)\), que es\(\ -21 t^{5}+\left(9 t^{4}\right)+\left(3 t^{3}\right)\). Reescribir suma de términos con coeficientes negativos como resta da\(\ -21 t^{5}-9 t^{4}+3 t^{3}\).
- Incorrecto. El negativo debe distribuirse a todos los términos junto con el\(\ 3 t^{2}\). Esto cambia el signo de los términos medio y último. La respuesta correcta es\(\ -21 t^{5}-9 t^{4}+3 t^{3}\).
- Incorrecto. Por las leyes de los exponentes, se suman (no multiplican) exponentes al multiplicar:\(\ -3 t^{2} \cdot 7 t^{3}+\left(-3 t^{2}\right) \cdot 3 t^{2}+\left(-3 t^{2}\right) \cdot(-t)\) is\(\ -21 t^{5}+\left(-9 t^{4}\right)+\left(3 t^{3}\right)\). La respuesta correcta es\(\ -21 t^{5}-9 t^{4}+3 t^{3}\).
- Incorrecto. Debe distribuir el monomio a los tres términos en el polinomio, no sólo el primero:\(\ -3 t^{2} \cdot 7 t^{3}+\left(-3 t^{2}\right) \cdot 3 t^{2}+\left(-3 t^{2}\right) \cdot(-t)\). La respuesta correcta es\(\ -21 t^{5}-9 t^{4}+3 t^{3}\).
Producto de Dos Binomios
Ahora vamos a explorar multiplicar dos binomios. Una vez más, puedes dibujar un modelo de área para ayudar a darle sentido al proceso. Utilizarás cada binomio como una de las dimensiones de un rectángulo, y su producto como área.
El siguiente modelo muestra\(\ (x+4)(2 x+2)\):
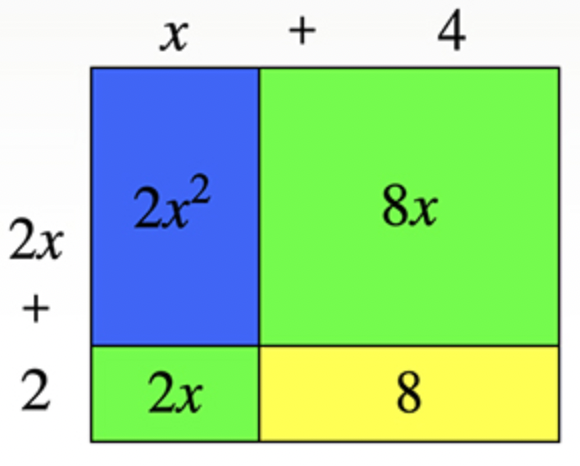
Cada binomio se expande en términos variables y constantes\(\ x+4\), a lo largo de la parte superior del modelo y\(\ 2 x+2\) a lo largo del lado izquierdo. El producto de cada par de términos es un rectángulo coloreado. El área total es la suma de todos estos pequeños rectángulos,\(\ 2 x^{2}+8 x+2 x+8\). Si combinas todos los términos similares, puedes escribir el producto, o área, como\(\ 2 x^{2}+10 x+8\).
Se puede utilizar la propiedad distributiva para determinar el producto de dos binomios.
\(\ (x+4)(2 x+2)\)
Solución
| \(\ x \cdot 2 x+x \cdot 2+4 \cdot 2 x+4 \cdot 2\) | Distribuya el\(\ x\) sobre\(\ 2 x+2\), luego distribuya 4 sobre\(\ 2 x+2\). |
| \(\ 2 x^{2}+2 x+8 x+8\) | Multiplicar. |
| \(\ 2 x^{2}+10 x+8\) | Combina términos similares\(\ (8 x+2 x)\). |
\(\ (x+4)(2 x+2)=2 x^{2}+10 x+8\)
Considera el modelo anterior para ver de dónde\(\ 2 x^{2}+8 x+2 x+8\) viene cada pieza de. ¿Puedes ver\(\ x\) por dónde te\(\ 2 x+2\) multiplicas y de dónde\(\ 2 x^{2}\) sacas\(\ x \cdot 2 x\)?
Otra forma de ver multiplicar binomios es ver que cada término en un binomio se multiplica por cada término en el otro binomio. En el ejemplo anterior, el\(\ x\) in\(\ x+4\) se multiplica tanto por el\(\ 2 x\) como por el 2 de\(\ 2 x+2\), y el 4 se multiplica tanto por el\(\ 2x\) como por el 2.
Algunas personas utilizan el método FOIL para realizar un seguimiento de qué pares se han multiplicado. Las letras en FOIL representan Primero, Exterior, Interior, Último:
Primer término en cada binomio:\(\ (\mathbf{x}+4)(\mathbf{2} \mathbf{x}+2)\mathrm{ x \cdot 2 x=2 x^{2}}\)
Términos externos:\(\ (\mathbf{x}+4)(2 \mathrm{x}+\mathbf 2)\mathrm{ x \cdot 2=2 x}\)
Términos internos:\(\ (\mathrm{x}+{\bf 4})({\bf 2 x}+2) 4 \cdot \mathrm{2 x=8 x}\)
Últimos términos en cada binomio:\(\ (\mathrm{x}+{\bf 4})( 2 \mathrm{x}+{\bf 2}) 4 \cdot 2=8\)
Cuando agregas los cuatro resultados, obtienes la misma respuesta:
\(\ 2 x^{2}+2 x+8 x+8=2 x^{2}+10 x+8\)
Aquí hay otro ejemplo, usando FOIL esta vez.
\(\ (4 x-10)(2 x+3)\)
Solución
| \ (\\ begin {array} {r} 4 x\ cdot 2 x=8 x^ {2}\ texto {(Primero)}\\ 4 x\ cdot 3=12 x\ texto {(Exterior)}\\ -10\ cdot 2 x=-20 x\ texto {(Interior)}\\ -10\ cdot 3=-30\ texto {(Último)} \ fin {matriz}\) |
Tenga cuidado al incluir el signo negativo en el -10, ya que se resta 10. |
| \(\ 8 x^{2}+12 x-20 x-30\) | Combina términos similares. |
\(\ (4 x-10)(2 x+3)=8 x^{2}-8 x-30\)
Debido a que la multiplicación es conmutativa, los términos se pueden multiplicar en cualquier orden. La expresión\(\ (2 x+2)(x+4)\) tiene el mismo producto que\(\ (x+4)(2 x+2)\),\(\ 2 x^{2}+10 x+8\). (Resuértelo y vea.) El orden en el que multiplicas los binomios no importa. Lo que importa es que multipliques cada término en un binomio por cada término en el otro binomio.
El último paso para multiplicar polinomios es combinar términos similares. Recuerda que un polinomio se simplifica sólo cuando no quedan términos similares.
Encuentra el producto:\(\ (a+10)(2 a-7)\)
- \(\ 2 a^{2}+19 a-70\)
- \(\ 3 a+3\)
- \(\ 2 a^{2}-70\)
- \(\ 2 a^{2}+13 a-70\)
- Contestar
-
- Incorrecto. El término medio debe ser\(\ 20 a-7 a\), que es\(\ 13 a\). La respuesta correcta es\(\ 2 a^{2}+13 a-70\).
- Incorrecto. Multiplique, no agregue, los términos en un binomio por los términos en el otro binomio. La respuesta correcta es\(\ 2 a^{2}+13 a-70\).
- Incorrecto. Multiplicar cada término en un binomio por los términos del otro binomio. \(\ \text { (a) }(-7)\)y\(\ (10)(2 a)\) faltan. La respuesta correcta es\(\ 2 a^{2}+13 a-70\).
- Correcto. Usando el método FOIL, encontrará:\(\ (a+10)(2 a-7)=a \cdot 2 a+a \cdot-7+10 \cdot 2 a+10 \cdot-7=2 a^{2}-7 a+20 a-70=2 a^{2}+13 a-70\).
Producto de un binomio y un trinomio
Otro tipo de problema de multiplicación polinómica es el producto de un binomio y un trinomio. Aunque el método FOIL no se puede utilizar exactamente ya que hay más de dos términos en un trinomio, todavía se utiliza la propiedad distributiva para organizar los productos individuales. Usando la propiedad distributiva, cada término en el binomio debe ser multiplicado por cada uno de los términos en el trinomio. A continuación se muestran dos ejemplos.
\(\ (3 x+6)\left(5 x^{2}+3 x+10\right)\)
Solución
| \(\ 3 x\left(5 x^{2}+3 x+10\right)+6\left(5 x^{2}+3 x+10\right)\) | Distribuir el trinomio a cada término en el binomio. |
| \(\ 3 x \cdot 5 x^{2}+3 x \cdot 3 x+3 x \cdot 10+6 \cdot 5 x^{2}+6 \cdot 3 x+6 \cdot 10\) | Utilizar la propiedad distributiva para distribuir los monomios a cada término en los trinomios. |
| \(\ 15 x^{3}+9 x^{2}+30 x+30 x^{2}+18 x+60\) | Multiplicar. |
| \(\ 15 x^{3}+\left(9 x^{2}+30 x^{2}\right)+(30 x+18 x)+60\) | Agrupar términos similares. |
| \(\ (3 x+6)\left(5 x^{2}+3 x+10\right)=15 x^{3}+39 x^{2}+48 x+60\) | Combina términos similares. |
Como puedes ver, ¡multiplicar un binomio por un trinomio lleva a muchos términos individuales! Algunas personas prefieren configurar estos problemas verticalmente y reunir como términos a medida que se multiplican. Este método se muestra a continuación, utilizando el mismo problema que el anterior.
\(\ (3 x+6)\left(5 x^{2}+3 x+10\right)\)
Solución
| \ (\\ begin {array} {rrr} 3 x +\\ 6\ \ veces\ quad 5 x^ {2} +\ 3 x +10\ \ hline +30 x +60 \ end {array}\) |
Configura el problema en forma vertical, y comienza multiplicando\(\ 3 x+6\) por\(\ +10\). Coloque los productos debajo, como se muestra. |
| \ (\\ comenzar {matriz} {r} 3 x +\\\ 6\ \ veces\ cuádruple x^ {2} +\\ {\ color {azul} 3 x} +10\ \\ hline +\ 30 x +60\ \\\ color {azul} +9 x^ {2} +18 x\\\\\\\ \ fin {matriz}\) |
Ahora multiplicar\(\ 3 x+6\) por\(\ 3x\). Observe eso\(\ \text { (6) }(3 x)=18 x\); ya que este término es como\(\ 30x\), colóquelo directamente debajo de él. |
| \ (\\ comenzar {array} {r} 3 x +\\\ 6\ \ veces\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple {\ color {verde} 5 x^ {2}} +\ \ 3 x +10\\\ hline +\\ 30 x +60\\ +\\ 9 x^ {2} +18 x\\\\\ \ {\ color {verde} +15 x^ {3} +30 x^ {2}}\\\\\\\\\\\\\\\\\\\\\\\ \ hline \ end {array}\\) |
Por último, multiplicar\(\ 3 x+6\) por\(\ 5 x^{2}\). Observe que\(\ 30 x^{2}\) se coloca debajo\(\ 9 x^{2}\). |
| \ (\\ comenzar {matriz} {r} 3 x +\\ 6\\ veces \ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple 5 x^ {2} +\ \ 3 x +10\\\ hline \ +30 x +60\\\ +\\ 9 x^ {2} +18 x\\\\\\ \ +15 x^ {3} +30 x^ {2}\\\\\\\\\\\\\\\\\\\ hline \ +15 x^ {3} +39 x^ {2} +48 x +60 \ final {matriz}\) |
Ahora agrega términos similares. |
\(\ 15 x^{3}+39 x^{2}+48 x+60\)
Observe que aunque los dos problemas se resolvieron usando diferentes estrategias, el producto es el mismo. Tanto el método horizontal como el vertical aplican la propiedad distributiva para multiplicar un binomio por un trinomio.
El siguiente ejemplo muestra la multiplicación por un binomio y trinomio que cada uno contiene resta. El ejemplo completa la multiplicación sin reescribir cada resta como suma de lo contrario. ¡Observe dónde debe tener cuidado con las señales! (Si lo prefieres, puedes continuar reescribiendo la resta como sumando lo contrario).
\(\ (2 p-1)\left(3 p^{2}-3 p+1\right)\)
Solución
| \(\ 2 p\left(3 p^{2}-3 p+1\right)-1\left(3 p^{2}-3 p+1\right)\) | Distribuir el trinomio a cada término en el binomio. |
| \(\ 2 p \cdot 3 p^{2}+2 p \cdot-3 p+2 p \cdot 1-1\left(3 p^{2}\right)-1(-3 p)-1(1)\) | Si no escribes resta como sumar lo contrario, entonces asegúrate de pensarlo de esa manera. Entonces estás distribuyendo -1 y multiplicando cada término del trinomio por -1. |
| \(\ 6 p^{3}-6 p^{2}+2 p-3 p^{2}+3 p-1\) | Multiplicar. (Observe que el 1 restado y el restado\(\ 3p\) tienen un producto positivo que se agrega.) |
| \(\ 6 p^{3}-9 p^{2}+5 p-1\) | Combina términos similares. |
\(\ 6 p^{3}-9 p^{2}+5 p-1\)
Encuentra el producto:\(\ (3 x-2)\left(2 x^{2}+4 x-11\right)\)
- \(\ 6 x^{3}+8 x^{2}-41 x+22\)
- \(\ 6 x^{3}+8 x^{2}-41 x-22\)
- \(\ 6 x^{3}+12 x+22\)
- \(\ 3 x^{3}+8 x^{2}+25 x-22\)
- Contestar
-
- Correcto. \(\ 3 x\left(2 x^{2}+4 x-11\right)-2\left(2 x^{2}+4 x-11\right)=6 x^{3}+12 x^{2}-33 x-4 x^{2}-8 x+22=6 x^{3}+8 x^{2}-41 x+22\)
- Incorrecto. \(\ (-2)(-11)=22\). La respuesta correcta es\(\ 6 x^{3}+8 x^{2}-41 x+22\).
- Incorrecto. Cada término en el binomio debe ser multiplicado por cada término en el trinomio. La respuesta correcta es\(\ 6 x^{3}+8 x^{2}-41 x+22\).
- Incorrecto. Multiplique los coeficientes\(\ (3 x)\left(2 x^{2}\right)\); combine términos similares sumar/restando coeficientes según sus signos. La respuesta correcta es\(\ 6 x^{3}+8 x^{2}-41 x+22\).
Resumen
La multiplicación de binomios y polinomios requiere el uso de la propiedad distributiva así como las propiedades conmutativas y asociativas de la multiplicación. Ya sea que los polinomios sean monomios, binomios o trinomios, multiplica cuidadosamente cada término en un polinomio por cada término en el otro polinomio. Tenga cuidado de observar los signos de suma y resta y los coeficientes negativos. Un producto se escribe en forma simplificada si todos sus términos similares se han combinado.