12.2: Vectores en tres dimensiones
- Page ID
- 116105
- Describir matemáticamente el espacio tridimensional.
- Localizar puntos en el espacio usando coordenadas.
- Escribe la fórmula de distancia en tres dimensiones.
- Escribe las ecuaciones para planos y esferas simples.
- Realizar operaciones vectoriales en\(\mathbb{R}^{3}\).
Los vectores son herramientas útiles para resolver problemas bidimensionales. La vida, sin embargo, ocurre en tres dimensiones. Para ampliar el uso de vectores a aplicaciones más realistas, es necesario crear un marco para describir el espacio tridimensional. Por ejemplo, aunque un mapa bidimensional es una herramienta útil para navegar de un lugar a otro, en algunos casos la topografía del terreno es importante. ¿Tu ruta planificada pasa por las montañas? ¿Tienes que cruzar un río? Para apreciar plenamente el impacto de estas características geográficas, se deben utilizar tres dimensiones. Esta sección presenta una extensión natural del plano de coordenadas cartesianas bidimensionales en tres dimensiones.
Sistemas de coordenadas tridimensionales
Como hemos aprendido, el sistema de coordenadas rectangulares bidimensionales contiene dos ejes perpendiculares: el\(x\) eje horizontal y el \(y\)eje vertical. Podemos agregar una tercera dimensión, el\(z\) eje -que es perpendicular tanto al\(x\) eje -como al eje\(y\) -eje. Llamamos a este sistema el sistema de coordenadas rectangulares tridimensionales. Representa las tres dimensiones que encontramos en la vida real.
El sistema de coordenadas rectangulares tridimensionales consta de tres ejes perpendiculares: el\(x\) eje -eje, el\(y\) eje -y el\(z\) eje -eje. Debido a que cada eje es una línea numérica que representa todos los números reales en\(ℝ\), el sistema tridimensional a menudo se denota por\(ℝ^3\).
En la Figura\(\PageIndex{1a}\), el \(z\)eje positivo se muestra por encima del plano que contiene los\(y\) ejes\(x\) - y -. El\(x\) eje positivo aparece a la izquierda y el\(y\) eje positivo está a la derecha. Una pregunta natural que hacer es: ¿Cómo se determinó este arreglo? El sistema que se muestra sigue la regla de la derecha. Si tomamos nuestra mano derecha y alineamos los dedos con el\(x\) eje positivo, entonces rizamos los dedos para que apunten en la dirección del \(y\)eje positivo, nuestro pulgar apunta en la dirección del\(z\) eje positivo (Figura\(\PageIndex{1b}\)). En este texto, siempre trabajamos con sistemas de coordenadas establecidos de acuerdo con la regla de la derecha. Algunos sistemas siguen una regla de la izquierda, pero la regla de la derecha se considera la representación estándar.
En dos dimensiones, describimos un punto en el plano con las coordenadas\((x,y)\). Cada coordenada describe cómo el punto se alinea con el eje correspondiente. En tres cotas, se agrega una nueva coordenada\(z\),, para indicar alineación con el\(z\) eje -eje:\((x,y,z)\). Un punto en el espacio se identifica por las tres coordenadas (Figura\(\PageIndex{2}\)). Para trazar el punto\((x,y,z)\), vaya\(x\) unidades a lo largo del \(x\)eje -eje, luego \(y\)unidades en la dirección del\(y\) eje -y luego\(z\) unidades en la dirección del\(z\) eje -eje.
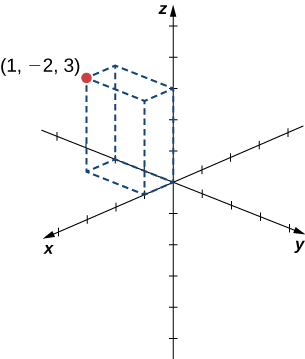
Dibuje el punto\((1,−2,3)\) en el espacio tridimensional.
Solución
Para esbozar un punto, comience dibujando tres lados de un prisma rectangular a lo largo de los ejes de coordenadas: una unidad en la\(x\) dirección positiva,\(2\) unidades en la\(y\) dirección negativa y\(3\) unidades en la\(z\) dirección positiva. Completar el prisma para trazar el punto (Figura\(\PageIndex{3}\)).
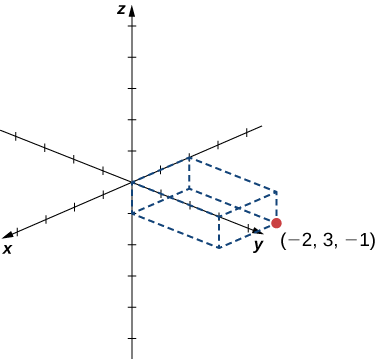
Dibuje el punto\((−2,3,−1)\) en el espacio tridimensional.
- Pista
-
Comience por esbozar los ejes de coordenadas. e.g., Figura\(\PageIndex{3}\). Después dibuja un prisma rectangular para ayudar a encontrar el punto en el espacio.
- Contestar
-
En el espacio bidimensional, el plano de coordenadas está definido por un par de ejes perpendiculares. Estos ejes nos permiten nombrar cualquier ubicación dentro del plano. En tres dimensiones, definimos planos de coordenadas por los ejes de coordenadas, al igual que en dos dimensiones. Ahora hay tres ejes, por lo que hay tres pares de ejes que se cruzan. Cada par de ejes forma un plano de coordenadas: el\(xy\) plano -plano, el \(xz\)-plano y el\(yz\) -plano (Figura\(\PageIndex{4}\)). Definimos el\(xy\) -plano formalmente como el siguiente conjunto:\(\{(x,y,0):x,y∈ℝ\}.\) Del mismo modo, el \(xz\)-plano y el\(yz\) -plano se definen como\(\{(x,0,z):x,z∈ℝ\}\) y\(\{(0,y,z):y,z∈ℝ\},\) respectivamente.
Para visualizar esto, imagina que estás construyendo una casa y estás parado en una habitación con solo dos de las cuatro paredes terminadas. (Supongamos que los dos muros terminados son adyacentes entre sí.) Si te paras de espaldas a la esquina donde se encuentran las dos paredes terminadas, mirando hacia la habitación, el piso es el\(xy\) plano, la pared a tu derecha es el \(xz\)plano, y la pared a tu izquierda es el \(yz\)plano.
En dos dimensiones, los ejes de coordenadas dividen el plano en cuatro cuadrantes. De igual manera, los planos de coordenadas dividen el espacio entre ellos en ocho regiones alrededor del origen, llamadas octantes. Los octantes se llenan\(ℝ^3\) de la misma manera que se llenan los cuadrantes\(ℝ^2\), como se muestra en la Figura\(\PageIndex{5}\).
La mayor parte del trabajo en el espacio tridimensional es una cómoda extensión de los conceptos correspondientes en dos dimensiones. En esta sección, utilizamos nuestro conocimiento de los círculos para describir esferas, luego expandimos nuestra comprensión de los vectores a tres dimensiones. Para lograr estos objetivos, comenzamos adaptando la fórmula de distancia al espacio tridimensional.
Si dos puntos se encuentran en el mismo plano de coordenadas, entonces es sencillo calcular la distancia entre ellos. Sabemos que la distancia\(d\) entre dos puntos\((x_1,y_1)\) y\((x_2,y_2)\) en el plano\(xy\) -coordenada viene dada por la fórmula
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
La fórmula para la distancia entre dos puntos en el espacio es una extensión natural de esta fórmula.
La distancia\(d\) entre puntos\((x_1,y_1,z_1)\) y\((x_2,y_2,z_2)\) viene dada por la fórmula
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}. \label{distanceForm} \]
La prueba de este teorema se deja como ejercicio. (Pista: Primero encuentra la distancia\(d_1\) entre los puntos\((x_1,y_1,z_1)\) y\((x_2,y_2,z_1)\) como se muestra en la Figura\(\PageIndex{6}\).)
Encuentra la distancia entre puntos\(P_1=(3,−1,5)\) y\(P_2=(2,1,−1).\)
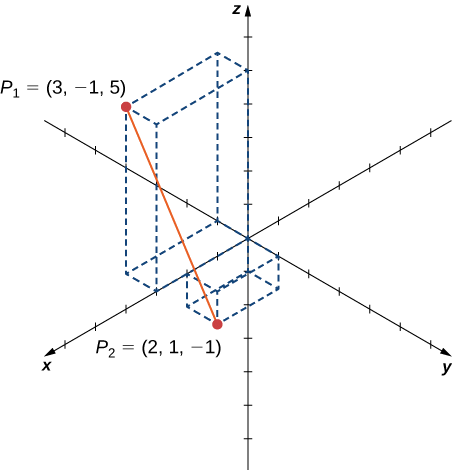
Solución
Sustituya los valores directamente en la fórmula de distancia (Ecuación\ ref {distanceForm}):
\[\begin{align*} d(P_1,P_2) &=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \\[4pt] &=\sqrt{(2−3)^2+(1−(−1))^2+(−1−5)^2} \\[4pt] &=\sqrt{(-1)^2+2^2+(−6)^2} \\[4pt] &=\sqrt{41}. \end{align*}\]
Encuentra la distancia entre puntos\(P_1=(1,−5,4)\) y\(P_2=(4,−1,−1)\).
- Pista
-
\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}\)
- Contestar
-
\(5\sqrt{2}\)
Antes de pasar a la siguiente sección, vamos a tener una idea de cómo\(ℝ^3\) difiere de\(ℝ^2\). Por ejemplo, en\(ℝ^2\), las líneas que no son paralelas deben cruzarse siempre. Este no es el caso en\(ℝ^3\). Por ejemplo, considere las líneas que se muestran en la Figura\(\PageIndex{8}\). Estas dos líneas no son paralelas, ni se cruzan.
Figura\(\PageIndex{8}\): Estas dos líneas no son paralelas, pero aún no se cruzan.
También se pueden tener círculos que están interconectados pero que no tienen puntos en común, como en la Figura\(\PageIndex{9}\).
Figura\(\PageIndex{9}\): Estos círculos están interconectados, pero no tienen puntos en común.
Tenemos mucha más flexibilidad trabajando en tres dimensiones que si nos quedamos con solo dos dimensiones.
Escribir ecuaciones en\(ℝ^3\)
Ahora que podemos representar puntos en el espacio y encontrar la distancia entre ellos, podemos aprender a escribir ecuaciones de objetos geométricos como líneas, planos y superficies curvas en\(ℝ^3\). Primero, comenzamos con una ecuación simple. Compare las gráficas de la ecuación\(x=0\) en\(ℝ\)\(ℝ^2\), y\(ℝ^3\) (Figura\(\PageIndex{10}\)). A partir de estas gráficas, podemos ver la misma ecuación que puede describir un punto, una línea, o un plano.
En el espacio, la ecuación\(x=0\) describe todos los puntos\((0,y,z)\). Esta ecuación define el\(yz\) -plano. Del mismo modo, el\(xy\) plano -contiene todos los puntos de la forma\((x,y,0)\). La ecuación\(z=0\) define el \(xy\)plano y la ecuación\(y=0\) describe el\(xz\) plano (Figura\(\PageIndex{11}\)).
Comprender las ecuaciones de los planos de coordenadas nos permite escribir una ecuación para cualquier plano que sea paralelo a uno de los planos de coordenadas. Cuando un plano es paralelo al \(xy\)-plano, por ejemplo, la coordenada\(z\) - de cada punto del plano tiene el mismo valor constante. Sólo las coordenadas\(x\) \(y\)- y - de puntos en ese plano varían de punto a punto.
- El plano en el espacio que es paralelo al\(xy\) -plano y contiene punto\((a,b,c)\) puede ser representado por la ecuación\(z=c\).
- El plano en el espacio que es paralelo al\(xz\) -plano y contiene punto\((a,b,c)\) puede ser representado por la ecuación\(y=b\).
- El plano en el espacio que es paralelo al\(yz\) -plano y contiene punto\((a,b,c)\) puede ser representado por la ecuación\(x=a\).
- Escribe una ecuación del plano que pasa a través del punto\((3,11,7)\) que es paralelo al\(yz\) plano.
- Encuentra una ecuación del plano que pasa por puntos\((6,−2,9), (0,−2,4),\) y\((1,−2,−3).\)
Solución
- Cuando un plano es paralelo al\(yz\) plano, solo las\(z\) coordenadas \(y\)- y -pueden variar. La\(x\) coordenada -tiene el mismo valor constante para todos los puntos de este plano, por lo que este plano puede ser representado por la ecuación\(x=3\).
- Cada uno de los puntos\((6,−2,9), (0,−2,4),\) y\((1,−2,−3)\) tiene la misma \(y\)- coordenada. Este plano puede ser representado por la ecuación\(y=−2\).
Escribe una ecuación del plano que pasa a través del punto\((1,−6,−4)\) que es paralelo al\(xy\) plano.
- Pista
-
Si un plano es paralelo al\(xy\) -plano, las coordenadas z- de los puntos en ese plano no varían.
- Contestar
-
\(z=−4\)
Como hemos visto, en\(ℝ^2\) la ecuación se\(x=5\) describe la línea vertical que pasa por el punto\((5,0)\). Esta línea es paralela al\(y\) eje -eje. En una extensión natural, la ecuación\(x=5\) en\(ℝ^3\) describe el plano que pasa por el punto\((5,0,0)\), que es paralelo al \(yz\)plano -plano. Otra extensión natural de una ecuación familiar se encuentra en la ecuación de una esfera.
Una esfera es el conjunto de todos los puntos en el espacio equidistantes de un punto fijo, el centro de la esfera (Figura\(\PageIndex{12}\)), así como el conjunto de todos los puntos en un plano que son equidistantes del centro representa un círculo. En una esfera, como en un círculo, la distancia desde el centro hasta un punto de la esfera se llama radio.
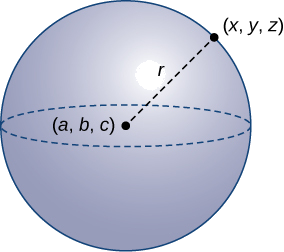
La ecuación de un círculo se deriva usando la fórmula de distancia en dos dimensiones. De la misma manera, la ecuación de una esfera se basa en la fórmula tridimensional para la distancia.
La esfera con centro\((a,b,c)\) y radio se\(r\) puede representar por la ecuación
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
Esta ecuación se conoce como la ecuación estándar de una esfera.
Encuentra la ecuación estándar de la esfera con centro\((10,7,4)\) y punto\((−1,3,−2)\), como se muestra en la Figura\(\PageIndex{13}\).
Figura\(\PageIndex{13}\): La esfera centrada en el punto de\((10,7,4)\) contención\((−1,3,−2).\)
Solución
Usa la fórmula de distancia para encontrar el radio\(r\) de la esfera:
\[\begin{align*} r &=\sqrt{(−1−10)^2+(3−7)^2+(−2−4)^2} \\[4pt] &=\sqrt{(−11)^2+(−4)^2+(−6)^2} \\[4pt] &=\sqrt{173} \end{align*} \nonumber \]
La ecuación estándar de la esfera es
\[(x−10)^2+(y−7)^2+(z−4)^2=173. \nonumber \]
Encuentra la ecuación estándar de la esfera con el centro\((−2,4,−5)\) que contiene el punto\((4,4,−1).\)
- Pista
-
Primero usa la fórmula de distancia para encontrar el radio de la esfera.
- Contestar
-
\[(x+2)^2+(y−4)^2+(z+5)^2=52 \nonumber \]
Dejar\(P=(−5,2,3)\) y\(Q=(3,4,−1)\), y supongamos que el segmento de línea\(\overline{PQ}\) forma el diámetro de una esfera (Figura\(\PageIndex{14}\)). Encuentra la ecuación de la esfera.
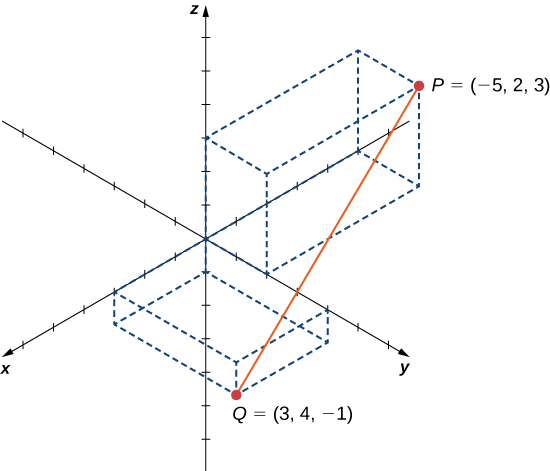
Solución:
Ya que\(\overline{PQ}\) es un diámetro de la esfera, sabemos que el centro de la esfera es el punto medio\(\overline{PQ}\) de.Entonces,
\[C=\left(\dfrac{−5+3}{2},\dfrac{2+4}{2},\dfrac{3+(−1)}{2}\right)=(−1,3,1). \nonumber \]
Además, sabemos que el radio de la esfera es la mitad de la longitud del diámetro. Esto da
\[\begin{align*} r &=\dfrac{1}{2}\sqrt{(−5−3)^2+(2−4)^2+(3−(−1))^2} \\[4pt] &=\dfrac{1}{2}\sqrt{64+4+16} \\[4pt] &=\sqrt{21} \end{align*}\]
Entonces, la ecuación de la esfera es\((x+1)^2+(y−3)^2+(z−1)^2=21.\)
Encuentra la ecuación de la esfera con diámetro\(\overline{PQ}\), donde\(P=(2,−1,−3)\) y\(Q=(−2,5,−1).\)
- Pista
-
Encuentra primero el punto medio del diámetro.
- Contestar
-
\[x^2+(y−2)^2+(z+2)^2=14 \nonumber \]
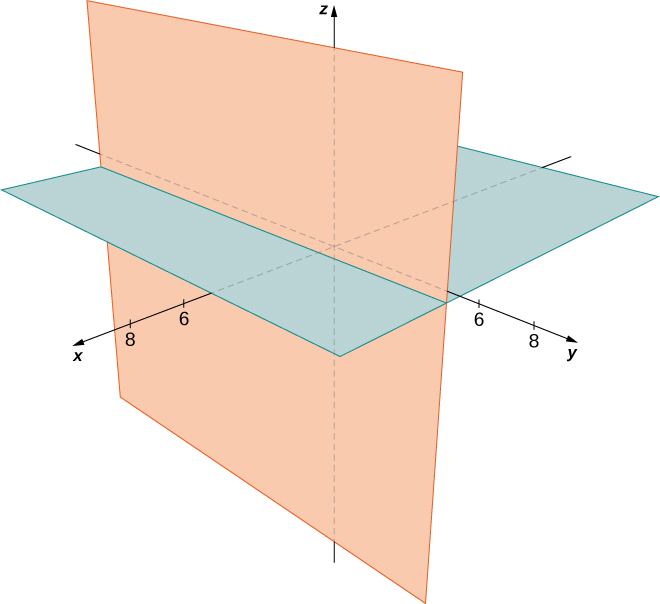
Describir el conjunto de puntos que satisface\((x−4)(z−2)=0,\) y grafica el conjunto.
Solución
Debemos tener cualquiera\(x−4=0\) o\(z−2=0\), así el conjunto de puntos forma los dos planos\(x=4\) y\(z=2\) (Figura\(\PageIndex{15}\)).
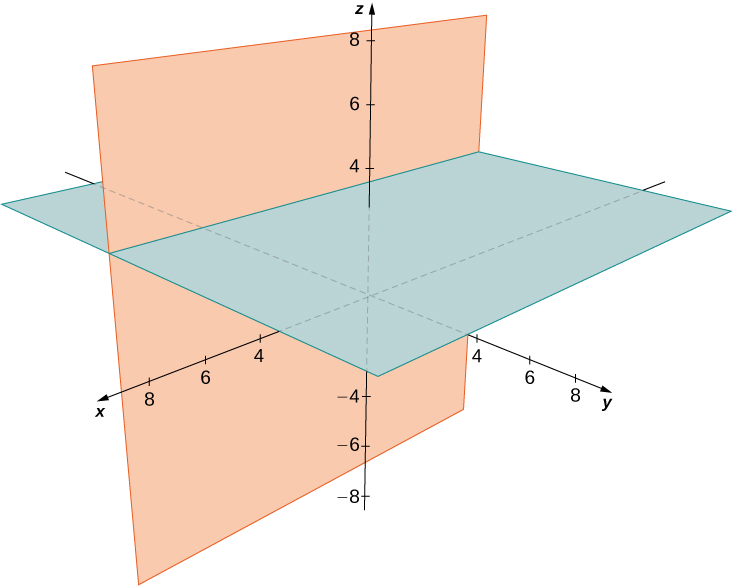
Describir el conjunto de puntos que satisface\((y+2)(z−3)=0,\) y grafica el conjunto.
- Pista
-
Uno de los factores debe ser cero.
- Contestar
-
El conjunto de puntos forma los dos planos\(y=−2\) y\(z=3\).
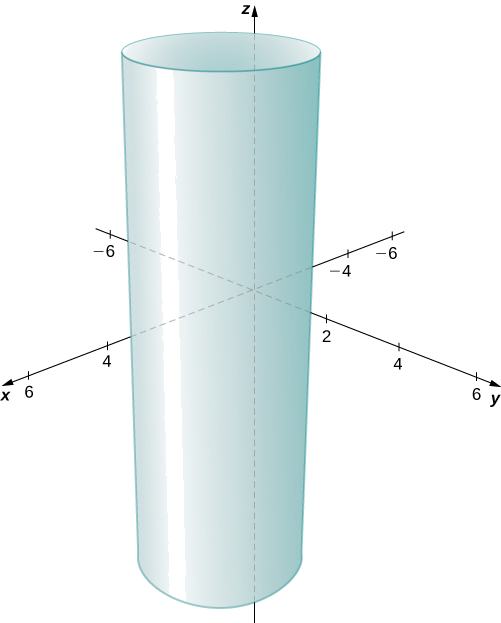
Describir el conjunto de puntos en el espacio tridimensional que satisface\((x−2)^2+(y−1)^2=4,\) y grafica el conjunto.
Solución
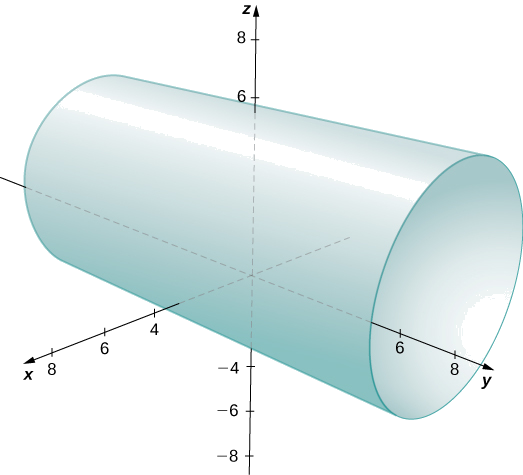
Las \(y\)coordenadas\(x\) - y -forman un círculo en el \(xy\)plano del radio\(2\), centrado en\((2,1)\). Dado que no hay restricción en la \(z\)coordenada -, el resultado tridimensional es un cilindro circular de radio\(2\) centrado en la línea con\(x=2\) y\(y=1\). El cilindro se extiende indefinidamente en la\(z\) dirección -dirección (Figura\(\PageIndex{16}\)).
Describir el conjunto de puntos en el espacio tridimensional que satisface\(x^2+(z−2)^2=16\) y grafica la superficie.
- Pista
-
Piensa en lo que sucede si trazas esta ecuación en dos dimensiones en el\(xz\) plano -.
- Contestar
-
Un cilindro de radio 4 centrado en la línea con\(x=0\) y\(z=2\).
Trabajar con vectores en\(ℝ^3\)
Al igual que los vectores bidimensionales, los vectores tridimensionales son cantidades con magnitud y dirección, y están representados por segmentos de línea dirigidos (flechas). Con un vector tridimensional, utilizamos una flecha tridimensional.
Los vectores tridimensionales también se pueden representar en forma de componentes. La notación\(\vecs{v}=⟨x,y,z⟩\) es una extensión natural del caso bidimensional, que representa un vector con el punto inicial en el origen\((0,0,0)\), y el punto terminal\((x,y,z)\). El vector cero es\(\vecs{0}=⟨0,0,0⟩\). Entonces, por ejemplo, el vector tridimensional\(\vecs{v}=⟨2,4,1⟩\) está representado por un segmento de línea dirigida de punto\((0,0,0)\) a punto\((2,4,1)\) (Figura\(\PageIndex{17}\)).
La adición de vectores y la multiplicación escalar se definen de manera análoga al caso bidimensional. Si\(\vecs{v}=⟨x_1,y_1,z_1⟩\) y\(\vecs{w}=⟨x_2,y_2,z_2⟩\) son vectores, y\(k\) es un escalar, entonces
\[\vecs{v}+\vecs{w}=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
y
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩. \nonumber \]
Si\(k=−1,\) entonces\(k\vecs{v}=(−1)\vecs{v}\) se escribe como\(−\vecs{v}\), y la resta vectorial se define por\(\vecs{v}−\vecs{w}=\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\).
Los vectores unitarios estándar también se extienden fácilmente en tres dimensiones,\(\hat{\mathbf i}=⟨1,0,0⟩\)\(\hat{\mathbf j}=⟨0,1,0⟩\), y\(\hat{\mathbf k}=⟨0,0,1⟩\), y, y los usamos de la misma manera que usamos los vectores unitarios estándar en dos dimensiones. Así, podemos representar un vector de\(ℝ^3\) las siguientes maneras:
\[\vecs{v}=⟨x,y,z⟩=x\hat{\mathbf i}+y\hat{\mathbf j}+z\hat{\mathbf k} \nonumber \].
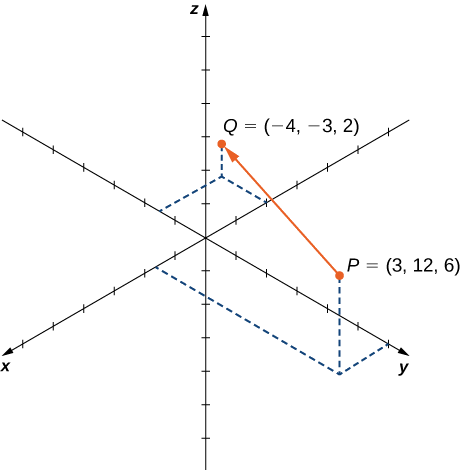
Dejar\(\vecd{PQ}\) ser el vector con punto inicial\(P=(3,12,6)\) y punto terminal\(Q=(−4,−3,2)\) como se muestra en la Figura\(\PageIndex{18}\). Expresar tanto\(\vecd{PQ}\) en forma de componente como usando vectores unitarios estándar.
Solución
En forma de componentes,
\[\begin{align*} \vecd{PQ} =⟨x_2−x_1,y_2−y_1,z_2−z_1⟩ \\[4pt] =⟨−4−3,−3−12,2−6⟩ \\[4pt] =⟨−7,−15,−4⟩. \end{align*}\]
En forma de unidad estándar,
\[\vecd{PQ}=−7\hat{\mathbf i}−15\hat{\mathbf j}−4\hat{\mathbf k}. \nonumber \]
Dejar\(S=(3,8,2)\) y\(T=(2,−1,3)\). Express\(\vec{ST}\) en forma de componentes y en forma de unidad estándar.
- Pista
-
Escriba primero\(\vecd{ST}\) en forma de componente. \(T\)es el punto terminal de\(\vecd{ST}\).
- Contestar
-
\(\vecd{ST}=⟨−1,−9,1⟩=−\hat{\mathbf i}−9\hat{\mathbf j}+\hat{\mathbf k}\)
Como se describió anteriormente, los vectores en tres dimensiones se comportan de la misma manera que los vectores en un plano. La interpretación geométrica de la adición vectorial, por ejemplo, es la misma tanto en el espacio bidimensional como en el tridimensional (Figura\(\PageIndex{19}\)).
Ya hemos visto cómo algunas de las propiedades algebraicas de los vectores, como la adición de vectores y la multiplicación escalar, pueden extenderse a tres dimensiones. Otras propiedades se pueden extender de manera similar. Se resumen aquí para nuestra referencia.
Dejar\(\vecs{v}=⟨x_1,y_1,z_1⟩\) y\(\vecs{w}=⟨x_2,y_2,z_2⟩\) ser vectores, y dejar\(k\) ser un escalar.
- Multiplicación escalar:\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
- Adición de vectores:\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
- Resta vectorial:\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
- Magnitud del vector:\[\|\vecs{v}\|=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
- Vector unitario en la dirección de\(\vecs{v}\):\[\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\|\vecs{v}\|}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{\|\vecs{v}\|},\dfrac{y_1}{\|\vecs{v}\|},\dfrac{z_1}{\|\vecs{v}\|}⟩, \quad \text{if} \, \vecs{v}≠\vecs{0} \nonumber \]
Hemos visto que la adición de vectores en dos dimensiones satisface las propiedades conmutativas, asociativas y aditivas inversas. Estas propiedades de las operaciones vectoriales también son válidas para vectores tridimensionales. La multiplicación escalar de vectores satisface la propiedad distributiva, y el vector cero actúa como una identidad aditiva. Las pruebas para verificar estas propiedades en tres dimensiones son extensiones directas de las pruebas en dos dimensiones.
Dejar\(\vecs{v}=⟨−2,9,5⟩\) y\(\vecs{w}=⟨1,−1,0⟩\) (Figura\(\PageIndex{20}\)). Encuentra los siguientes vectores.
- \(3\vecs{v}−2\vecs{w}\)
- \(5\|\vecs{w}\|\)
- \(\|5 \vecs{w}\|\)
- Un vector unitario en la dirección de\(\vecs{v}\)
Solución
a. Primero, use la multiplicación escalar de cada vector, luego restar:
\[\begin{align*} 3\vecs{v}−2\vecs{w} =3⟨−2,9,5⟩−2⟨1,−1,0⟩ \\[4pt] =⟨−6,27,15⟩−⟨2,−2,0⟩ \\[4pt] =⟨−6−2,27−(−2),15−0⟩ \\[4pt] =⟨−8,29,15⟩. \end{align*}\]
b. Escribe la ecuación para la magnitud del vector, luego usa la multiplicación escalar:
\[5\|\vecs{w}\|=5\sqrt{1^2+(−1)^2+0^2}=5\sqrt{2}. \nonumber \]
c. Primero, usa la multiplicación escalar, luego encontrar la magnitud del nuevo vector. Tenga en cuenta que el resultado es el mismo que para la parte b.:
\[\|5 \vecs{w}\|=∥⟨5,−5,0⟩∥=\sqrt{5^2+(−5)^2+0^2}=\sqrt{50}=5\sqrt{2} \nonumber \]
d. Recordemos que para encontrar un vector unitario en dos dimensiones, dividimos un vector por su magnitud. El procedimiento es el mismo en tres dimensiones:
\[\begin{align*} \dfrac{\vecs{v}}{\|\vecs{v}\|} =\dfrac{1}{\|\vecs{v}\|}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{(−2)^2+9^2+5^2}}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{110}}⟨−2,9,5⟩ \\[4pt] =⟨\dfrac{−2}{\sqrt{110}},\dfrac{9}{\sqrt{110}},\dfrac{5}{\sqrt{110}}⟩ . \end{align*}\]
Dejar\(\vecs{v}=⟨−1,−1,1⟩\) y\(\vecs{w}=⟨2,0,1⟩\). Encuentra un vector de unidad en la dirección de\(5\vecs{v}+3\vecs{w}.\)
- Pista
-
Comience por escribir\(5\vecs{v}+3\vecs{w}\) en forma de componentes.
- Contestar
-
\(⟨\dfrac{1}{3\sqrt{10}},−\dfrac{5}{3\sqrt{10}},\dfrac{8}{3\sqrt{10}}⟩\)
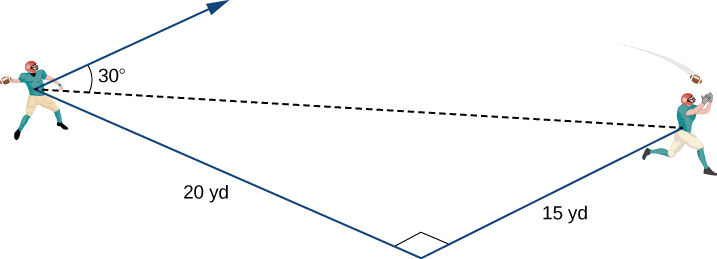
Un mariscal de campo se encuentra parado en el campo de fútbol preparándose para lanzar un pase. Su receptor está parado 20 yd abajo del campo y 15 yd a la izquierda del mariscal de campo. El mariscal de campo lanza el balón a una velocidad de 60 mph hacia el receptor en un ángulo ascendente de\(30°\) (ver la siguiente figura). Escribe el vector de velocidad inicial de la bola,\(\vecs{v}\), en forma de componente.
Solución
Lo primero que queremos hacer es encontrar un vector en la misma dirección que el vector de velocidad de la pelota. Luego escalamos el vector apropiadamente para que tenga la magnitud correcta. Considera el vector\(\vecs{w}\) que se extiende desde el brazo del mariscal de campo hasta un punto directamente por encima de la cabeza del receptor en un ángulo de\(30°\) (ver la siguiente figura). Este vector tendría la misma dirección que\(\vecs{v}\), pero puede que no tenga la magnitud correcta.
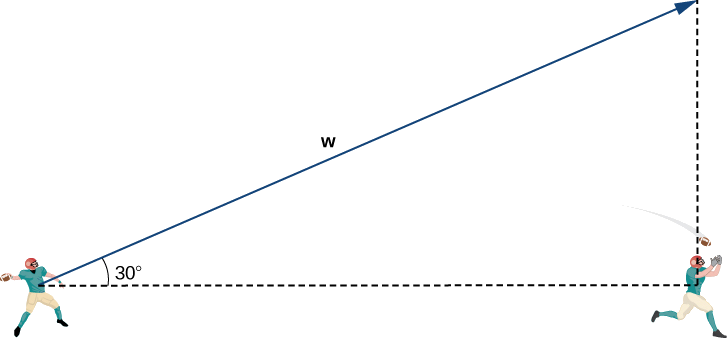
El receptor está 20 yd abajo del campo y 15 yd a la izquierda del mariscal de campo. Por lo tanto, la distancia en línea recta del mariscal de campo al receptor es
Dist de QB al receptor\(=\sqrt{15^2+20^2}=\sqrt{225+400}=\sqrt{625}=25\) yd.
Tenemos\(\dfrac{25}{\|\vecs{w}\|}=\cos 30°.\) Entonces la magnitud de\(\vecs{w}\) viene dada por
\(\|\vecs{w}\|=\dfrac{25}{\cos 30°}=\dfrac{25⋅2}{\sqrt{3}}=\dfrac{50}{\sqrt{3}}\)yd
y la distancia vertical desde el receptor hasta el punto terminal de\(\vecs{w}\) es
Vert dist del receptor al punto terminal de\(\vecs{w}=\|\vecs{w}\| \sin 30°=\dfrac{50}{\sqrt{3}}⋅\dfrac{1}{2}=\dfrac{25}{\sqrt{3}}\) yd.
Entonces\(\vecs{w}=⟨20,15,\dfrac{25}{\sqrt{3}}⟩\), y tiene la misma dirección que\(\vecs{v}\).
Recordemos, sin embargo, que calculamos la magnitud de\(\vecs{w}\) ser\(\|\vecs{w}\|=\dfrac{50}{\sqrt{3}}\) yd, y\(\vecs{v}\) tiene magnitud\(60\) mph. Entonces, necesitamos multiplicar vector\(\vecs{w}\) por una constante apropiada,\(k\). Queremos encontrar un valor de\(k\) para que\(∥k\vecs{w}∥=60\) mph *. Tenemos
\(\|k \vecs{w}\|=k\|\vecs{w}\|=k\dfrac{50}{\sqrt{3}}\)yd,
por lo que queremos
\(k \left(\dfrac{50}{\sqrt{3}}\text{ yd}\right) =60\)mph
\(k=\dfrac{60\sqrt{3}}{50}\)mph/yd
\(k=\dfrac{6\sqrt{3}}{5}\)mph/yd.
Entonces
\(\vecs{v}=k\vecs{w}=k⟨20,15,\dfrac{25}{\sqrt{3}}⟩=\dfrac{6\sqrt{3}}{5}\;⟨20,15,\dfrac{25}{\sqrt{3}}⟩=⟨24\sqrt{3},18\sqrt{3},30⟩\).
Vamos a verificar que\(\|\vecs{v}\|=60\) mph. Tenemos
\(\|\vecs{v}\|=\sqrt{(24\sqrt{3})^2+(18\sqrt{3})^2+(30)^2}=\sqrt{1728+972+900}=\sqrt{3600}=60\)mph.
Entonces, hemos encontrado los componentes correctos para\(\vecs{v}\).
Los lectores que han estado viendo las unidades de medida pueden preguntarse qué está pasando exactamente en este punto: ¿no hemos mezclado yardas y millas por hora? No lo hemos hecho, pero la razón es sutil. Una manera de entenderlo es darse cuenta de que en realidad hay dos sistemas de coordenadas paralelas en este problema: uno da posiciones abajo del campo, a través del campo, y arriba en el aire en unidades de yardas; el otro da velocidades abajo del campo, a través del campo, y hacia arriba en el aire en unidades de millas por hora. El vector\(\vecs{w}\) se calcula en el sistema de coordenadas de posición; el vector\(\vecs{v}\) estará en el sistema de velocidad. Debido a que los ejes correspondientes en cada sistema son paralelos, las direcciones en los dos sistemas también son paralelas, por lo que la afirmación de que\(\vecs{w}\) y\(\vecs{v}\) punto en la misma dirección es correcta. La constante\(k\) que estamos buscando es un factor de conversión entre las magnitudes de estos dos vectores, convirtiendo del sistema de posición al de velocidad uno en el proceso. Y como se vio anteriormente, nuestro cálculo de\(k\) produce las unidades adecuadas para tal conversión, es decir, millas por hora por yarda.
Supongamos que el quarterback y el receptor están en el mismo lugar que en el ejemplo anterior. Esta vez, sin embargo, el mariscal de campo lanza la pelota a una velocidad de\(40\) mph y un ángulo de\(45°\). Escribe el vector de velocidad inicial de la bola,\(\vecs{v}\), en forma de componente.
- Pista
-
Siga el proceso utilizado en el ejemplo anterior.
- Contestar
-
\(v=⟨16\sqrt{2},12\sqrt{2},20\sqrt{2}⟩\)
Conceptos clave
- El sistema de coordenadas tridimensional se construye alrededor de un conjunto de tres ejes que se cruzan en ángulo recto en un solo punto, el origen. Los triples ordenados se\((x,y,z)\) utilizan para describir la ubicación de un punto en el espacio.
- La distancia\(d\) entre puntos\((x_1,y_1,z_1)\) y\((x_2,y_2,z_2)\) viene dada por la fórmula\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}.\nonumber \]
- En tres dimensiones, las ecuaciones\(x=a,\, y=b,\) y\(z=c\) describen planos que son paralelos a los planos de coordenadas.
- La ecuación estándar de una esfera con centro\((a,b,c)\) y radio\(r\) es\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
- En tres dimensiones, como en dos, los vectores se expresan comúnmente en forma de componentes\(\vecs v=⟨x,y,z⟩\), o en términos de los vectores unitarios estándar,\(\vecs v= x\,\mathbf{\hat i}+y\,\mathbf{\hat j}+z\,\mathbf{\hat k}.\)
- Las propiedades de los vectores en el espacio son una extensión natural de las propiedades de los vectores en un plano. Dejar\(\vecs v=⟨x_1,y_1,z_1⟩\) y\(\vecs w=⟨x_2,y_2,z_2⟩\) ser vectores, y dejar\(k\) ser un escalar.
Multiplicación escalar:
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
Adición de vectores:
\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
Resta vectorial:
\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
Magnitud del vector:
\[‖\vecs{v}‖=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
Vector unitario en la dirección de\(\vecs{v}\):
\[\dfrac{\vecs{v}}{‖\vecs{v}‖}=\dfrac{1}{‖\vecs{v}‖}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{‖\vecs{v}‖},\dfrac{y_1}{‖\vecs{v}‖},\dfrac{z_1}{‖\vecs{v}‖}⟩, \; \vecs{v}≠\vecs{0} \nonumber \]
Ecuaciones Clave
Distancia entre dos puntos en el espacio:
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \nonumber \]
Esfera con centro\((a,b,c)\) y radio\(r\):
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2 \nonumber \]
Glosario
- plano de coordenadas
- un plano que contiene dos de los tres ejes de coordenadas en el sistema de coordenadas tridimensional, denominado por los ejes que contiene: el\(xy\) -plano,\(xz\) -plano o el\(yz\) -plano
- regla de la mano derecha
- una forma común de definir la orientación del sistema de coordenadas tridimensional; cuando la mano derecha se curva alrededor del\(z\) eje de tal manera que los dedos se curvan desde el\(x\) eje positivo al\(y\) eje positivo, el pulgar apunta en la dirección del\(z\) eje positivo
- octantes
- las ocho regiones del espacio creadas por los planos de coordenadas
- esfera
- el conjunto de todos los puntos equidistantes de un punto dado conocido como el centro
- ecuación estándar de una esfera
- \((x−a)^2+(y−b)^2+(z−c)^2=r^2\)describe una esfera con centro\((a,b,c)\) y radio\(r\)
- sistema de coordenadas rectangulares tridimensionales
- un sistema de coordenadas definido por tres líneas que se cruzan en ángulo recto; cada punto en el espacio es descrito por un triple ordenado\((x,y,z)\) que traza su ubicación relativa a los ejes definitorios
Colaboradores
Ejemplo\(\PageIndex{10}\) ha sido modificado por Doug Baldwin y Paul Seeburger para aclarar las unidades de medida que utiliza y cómo las usa.
Paul Seeburger también creó versiones dinámicas de Figures\(\PageIndex{8}, \PageIndex{9}\) y\(\PageIndex{13}\) usando CalcPlot3D.