13.2.3: Líneas paralelas y perpendiculares

Última actualización
Guardar como PDF

Page ID: 111549

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Encuentra la pendiente de una línea paralela o perpendicular a una línea existente.
Dado un punto y una línea perpendicular o paralela a la línea desconocida, escriba la ecuación de la línea desconocida.

Introducción

Cuando grafica dos o más ecuaciones lineales en un plano de coordenadas, generalmente se cruzan en un punto. Sin embargo, cuando dos líneas en un plano de coordenadas nunca se cruzan, se llaman líneas paralelas. También mirarás el caso donde dos líneas en un plano de coordenadas se cruzan en ángulo recto. Estas se llaman líneas perpendiculares. Las pendientes de las gráficas en cada uno de estos casos tienen una relación especial entre sí.

Exploración de líneas paralelas y perpendiculares

Las líneas paralelas son dos o más líneas en un plano que nunca se cruzan. Ejemplos de líneas paralelas están a nuestro alrededor, como los lados opuestos de un marco rectangular y los estantes de una estantería.

Las líneas perpendiculares son dos o más líneas que se cruzan en un ángulo de 90 grados, como las dos líneas dibujadas en esta gráfica. Estos ángulos de 90 grados también se conocen como ángulos rectos.

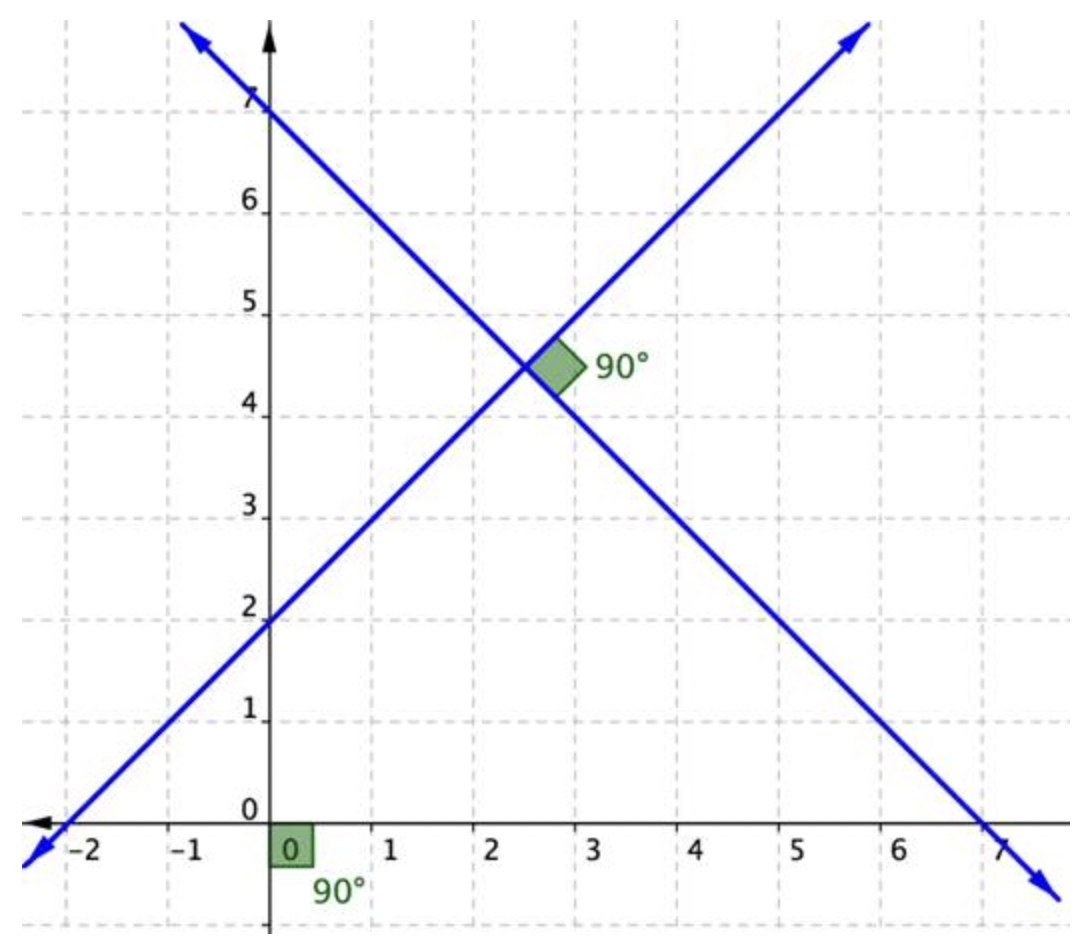
$Screen Shot 2021-06-28 a las 11.58.09 AM.png$

Las líneas perpendiculares también están en todas partes, no solo en papel cuadruculado sino también en el mundo que nos rodea, desde el patrón de cruce de caminos en una intersección hasta las líneas de colores de una camisa a cuadros.

Actividad interactiva suplementaria

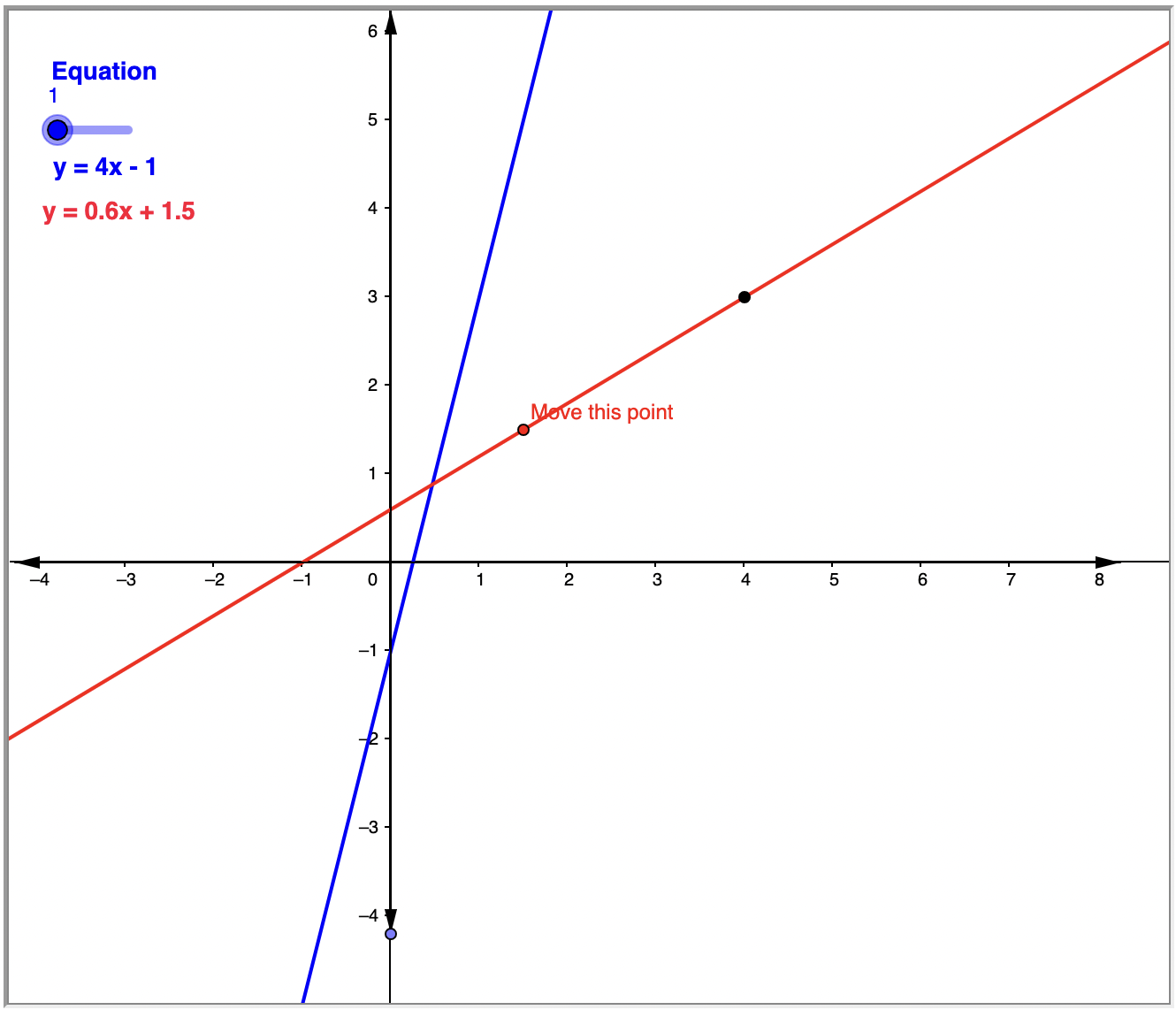
Explora líneas en el diagrama interactivo a continuación.

Haga clic y arrastre el punto en el control deslizante “Ecuación” para elegir una de las cinco ecuaciones de ejemplo. La ecuación se graficará en azul.
Después, haga clic y arrastre el punto en la línea roja para hacer que la línea sea paralela o perpendicular a la línea azul. (Asegúrese de mover el cursor lentamente). Cuando las líneas son paralelas o perpendiculares, aparecerá texto para hacerte saber que lo has hecho!
Mira las pendientes de las dos líneas paralelas. ¿Qué notas? Observa las pendientes de dos líneas perpendiculares. ¿Qué notas?
Elige otra ecuación e inténtalo de nuevo.
A medida que intentas más ecuaciones, busca la relación entre las pendientes de las líneas paralelas, y las pendientes para las líneas perpendiculares. Para la última ecuación que intentas, ¿puedes predecir cuáles deben ser las pendientes de las líneas paralelas y perpendiculares?

$Screen Shot 2021-06-28 a las 12.00.58 PM.png$

Tenga en cuenta lo siguiente:

Líneas Paralelas

Dos líneas no verticales en un plano son paralelas si tienen ambas:

la misma pendiente
diferentes intercepciones en Y

Dos líneas verticales cualesquiera en un plano son paralelas.

Ejemplo

Encuentra la pendiente de una línea paralela a la línea$\ y=-3 x+4$.

Solución

La línea dada está escrita en$\ y=m x+b$ forma, con$\ m=-3$ y$\ b=4$. La pendiente es -3	Identificar la pendiente de la línea dada.
La pendiente de la línea paralela es -3.	Una línea paralela a la línea dada tiene la misma pendiente.

Ejemplo

Determinar si las líneas$\ y=6 x+5$ y$\ y=6 x-1$ son paralelas.

Solución

Las líneas dadas están escritas en$\ y=m x+b$ forma, con$\ m=6$ para la primera línea y$\ m=6$ para la segunda línea. La pendiente de ambas líneas es de 6.	Identificar las pendientes de las líneas dadas.
La primera línea tiene una intersección y en$\ (0,5)$, y la segunda línea tiene una intersección en y en$\ (0,-1)$. No son la misma línea.	Mira$\ b$, el valor y de la intersección y, para ver si las líneas son quizás exactamente la misma línea, en cuyo caso no decimos que sean paralelas.
Las líneas son paralelas.	Las pendientes de las líneas son las mismas y tienen diferentes intercepciones y, por lo tanto, no son la misma línea y son paralelas.

Líneas perpendiculares

Dos líneas no verticales son perpendiculares si la pendiente de una es el recíproco negativo de la pendiente de la otra. Si la pendiente de la primera ecuación es 4, entonces la pendiente de la segunda ecuación tendrá que ser$\ -\frac{1}{4}$ para que las líneas sean perpendiculares.

También puedes revisar las dos pendientes para ver si las líneas son perpendiculares multiplicando las dos pendientes juntas. Si son perpendiculares, el producto de las pendientes será -1. Por ejemplo,$\ 4 \cdot-\frac{1}{4}=\frac{4}{1} \cdot-\frac{1}{4}=-1$.

Ejemplo

Encuentra la pendiente de una línea perpendicular a la línea$\ y=2 x-6$.

Solución

La línea dada está escrita en$\ y=m x+b$ forma, con$\ m=2$ y$\ b=-6$. La pendiente es 2.	Identificar la pendiente de la línea dada.
La pendiente de la línea perpendicular es$\ -\frac{1}{2}$.	Para encontrar la pendiente de una línea perpendicular, encontrar el recíproco,$\ \frac{1}{2}$, y luego encontrar lo contrario de este recíproco$\ -\frac{1}{2}$.

Tenga en cuenta que el producto$\ 2\left(-\frac{1}{2}\right)=\frac{2}{1}\left(-\frac{1}{2}\right)=-1$, por lo que esto significa que las pendientes son perpendiculares.

En el caso de que una de las líneas sea vertical, la pendiente de esa línea es indefinida y no es posible calcular el producto con un número indefinido. Cuando una línea es vertical, la línea perpendicular a ella será horizontal, teniendo una pendiente de cero$\ (m=0)$.

Ejemplo

Determinar si las líneas$\ y=-8 x+5$ y$\ y=\frac{1}{8} x-1$ son paralelas, perpendiculares o ninguna.

Solución

Las líneas dadas están escritas en$\ y=m x+b$ forma, con$\ m=-8$ para la primera línea y$\ m=\frac{1}{8}$ para la segunda línea.

Identificar las pendientes de las líneas dadas.

$\ -8 \neq \frac{1}{8}$, por lo que las líneas no son paralelas.

El recíproco opuesto de -8 es$\ \frac{1}{8}$, por lo que las líneas son perpendiculares.

Determinar si las pendientes son las mismas o si son recíprocas opuestas.

Las líneas son perpendiculares.

Las pendientes de las líneas son recíprocas opuestas, por lo que las líneas son perpendiculares.

Ejercicio

¿Cuáles de las siguientes líneas son perpendiculares a la línea$\ y=7 x+\frac{2}{3}$?

$\ y=-\frac{1}{7} x$

$\ y=-\frac{1}{7} x-12$

$\ y=\frac{1}{7} x-\frac{3}{2}$

$\ y=-7 x+\frac{3}{2}$

$\ y=-\frac{1}{7} x \text { and } y=-\frac{1}{7} x-12$
$\ y=-\frac{1}{7} x-12 \text { and } y=\frac{1}{7} x-\frac{3}{2}$
$\ y=-7 x+\frac{3}{2}$
Todas las líneas son perpendiculares.

Contestar

Correcto. Ambas líneas tienen una pendiente de$\ -\frac{1}{7}$, que es el recíproco opuesto de la pendiente de 7 en la ecuación original. Ambas líneas son perpendiculares a la línea original.
Incorrecto. Las líneas perpendiculares tienen pendientes que son opuestas a la recíproca de la otra. Sólo$\ -\frac{1}{7}$ es lo opuesto al recíproco de 7. La respuesta correcta es$\ y=-\frac{1}{7} x$ y$\ y=-\frac{1}{7} x-12$.
Incorrecto. Las líneas perpendiculares tienen pendientes que son lo opuesto al recíproco de la otra. -7 es lo opuesto de 7, pero no es lo opuesto al recíproco de 7. La respuesta correcta es$\ y=-\frac{1}{7} x$ y$\ y=-\frac{1}{7} x-12$.
Incorrecto. Sólo las líneas que tienen una pendiente de$\ -\frac{1}{7}$, que es lo opuesto al recíproco de 7, pueden ser perpendiculares a la ecuación original. La respuesta correcta es$\ y=-\frac{1}{7} x$ y$\ y=-\frac{1}{7} x-12$.

Escritura de líneas paralelas y perpendiculares

Las relaciones entre pendientes de líneas paralelas y perpendiculares se pueden utilizar para escribir ecuaciones de líneas paralelas y perpendiculares.

Empecemos con un ejemplo que involucra líneas paralelas.

Ejemplo

Escribe la ecuación de una línea que es paralela a la línea$\ x-y=5$ y pasa por el punto$\ (-2,1)$.

Solución

\ (\\ comenzar {alineado} x-y &=\\\\\\\\\\\ 5\ -y &=-x+5\\ y &=\\\ x -5 \ final {alineado}\)	Reescribe la línea a la que quieres que sea paralela en el$\ y=m x+b$ formulario, si es necesario.
En la ecuación anterior,$\ m=1$ y$\ b=-5$. Ya que$\ m=1$, la pendiente es 1.	Identificar la pendiente de la línea dada.
La pendiente de la línea paralela es 1.	Para encontrar la pendiente de una línea paralela, utilice la misma pendiente.
\ (\\ begin {array} {c} y=m x+b\\ 1=1 (-2) +b \ end {array}\)	Utilice el método para escribir una ecuación a partir de la pendiente y un punto en la línea. Sustituir 1 por$\ m$, y el punto$\ (-2,1)$ por$\ x$ y$\ y$.
\ (\\ begin {array} {c} 1=-2+b\ \ quad 3=b \ end {array}\)	Resolver para$\ b$.
$\ y=x+3$	Escribe la ecuación usando la nueva pendiente para$\ m$ y la$\ b$ que acabas de encontrar.

Cuando se trabaja con líneas perpendiculares, generalmente se le dará una de las líneas y un punto adicional.

Ejemplo

Escribe la ecuación de una línea que contiene el punto$\ (1,5)$ y es perpendicular a la línea$\ y=2 x-6$.

Solución

La línea dada está escrita en$\ y=m x+b$ forma, con$\ m=2$ y$\ b=-6$. La pendiente es 2.	Identifica la pendiente de la línea a la que quieres que sea perpendicular.
La pendiente de la línea perpendicular es$\ -\frac{1}{2}$.	Para encontrar la pendiente de una línea perpendicular, encontrar el recíproco,$\ \frac{1}{2}$, luego lo contrario,$\ -\frac{1}{2}$.
\ (\\ begin {array} {c} y=m x+b\ 5=-\ frac {1} {2} (1) +b \ end {array}\)	Utilice el método para escribir una ecuación a partir de la pendiente y un punto en la línea. Sustituto$\ -\frac{1}{2}$ de$\ m$, y el punto$\ (1,5)$ para$\ x$ y$\ y$.
\ (\\ begin {array} {c} 5=-\ frac {1} {2} +b\\ \ frac {11} {2} =b \ end {array}\)	Resolver para$\ b$.
$\ y=-\frac{1}{2} x+\frac{11}{2}$	Escribe la ecuación usando la nueva pendiente para$\ m$ y la$\ b$ que acabas de encontrar.

Ejercicio

¿Cuál de las siguientes es la ecuación de la línea que es paralela$\ y=-2 x-14$ y pasa por el punto$\ (-3,1)$?

$\ y=-2 x+1$
$\ y=\frac{1}{2} x+2 \frac{1}{2}$
$\ y=\frac{1}{2} x+1$
$\ y=-2 x-5$

Contestar

Incorrecto. Comprobando$\ (-3,1)$ en la ecuación da$\ 1=-2(-3)+1$, que es$\ 1=6+1$. Ya que$\ 6+1=7$, no 1, esta línea no puede pasar por el punto$\ (-3,1)$. La respuesta correcta es$\ y=-2 x-5$.
Incorrecto. Las líneas paralelas tienen la misma pendiente, por lo que esta ecuación también debe tener una pendiente de -2. La respuesta correcta es$\ y=-2 x-5$.
Incorrecto. Las líneas paralelas tienen la misma pendiente, por lo que esta ecuación también debe tener una pendiente de -2. La respuesta correcta es$\ y=-2 x-5$.
Correcto. La línea tiene la misma pendiente que la original, por lo que son paralelas. Comprobando$\ (-3,1)$ en la ecuación da$\ 1=-2(-3)-5$, o$\ 1=6-5$, que es cierto. La línea es paralela y pasa por el punto$\ (-3,1)$.

Ejemplo

Escribe la ecuación de una línea que sea paralela a la línea$\ y=4$.

Solución

\ (\\ begin {array} {c} y=4\\ y=0 x+4 \ end {array}\)	Vuelva a escribir la línea en$\ y=m x+b$ forma, si es necesario. Puede notar sin hacer esto que$\ y=4$ es una línea horizontal 4 unidades por encima del eje x. Debido a que es horizontal, sabes que su pendiente es cero.
En la ecuación anterior,$\ m=0$ y$\ b=4$. Ya que$\ m=0$, la pendiente es 0. Esta es una línea horizontal.	Identificar la pendiente de la línea dada.
La pendiente de la línea paralela también es 0.	Para encontrar la pendiente de una línea paralela, utilice la misma pendiente.
$\ y=10$	Dado que la línea paralela será una línea horizontal, su forma es$\ y=a$ constante. Elija una constante para encontrar una línea paralela.
$\ y=10$	Esta línea es paralela$\ y=4$ e interseca el eje y en$\ (0,10)$.

Resumen

Cuando las líneas en un plano son paralelas (es decir, nunca se cruzan), tienen la misma pendiente. Cuando las líneas son perpendiculares (es decir, se cruzan en un ángulo de 90 ^o), sus pendientes son recíprocas opuestas entre sí. El producto de sus pendientes será -1, excepto en el caso en que una de las líneas sea vertical, haciendo que su pendiente sea indefinida. Puede utilizar estas relaciones para encontrar una ecuación de una línea que pasa por un punto en particular y es paralela o perpendicular a otra línea.

La línea dada está escrita en\(\ y=m x+b\) forma, con\(\ m=2\) y\(\ b=-6\). La pendiente es 2.	Identificar la pendiente de la línea dada.
La pendiente de la línea perpendicular es\(\ -\frac{1}{2}\).	Para encontrar la pendiente de una línea perpendicular, encontrar el recíproco,\(\ \frac{1}{2}\), y luego encontrar lo contrario de este recíproco\(\ -\frac{1}{2}\).

La línea dada está escrita en\(\ y=m x+b\) forma, con\(\ m=2\) y\(\ b=-6\). La pendiente es 2.	Identifica la pendiente de la línea a la que quieres que sea perpendicular.
La pendiente de la línea perpendicular es\(\ -\frac{1}{2}\).	Para encontrar la pendiente de una línea perpendicular, encontrar el recíproco,\(\ \frac{1}{2}\), luego lo contrario,\(\ -\frac{1}{2}\).
\ (\\ begin {array} {c} y=m x+b\ 5=-\ frac {1} {2} (1) +b \ end {array}\)	Utilice el método para escribir una ecuación a partir de la pendiente y un punto en la línea. Sustituto\(\ -\frac{1}{2}\) de\(\ m\), y el punto\(\ (1,5)\) para\(\ x\) y\(\ y\).
\ (\\ begin {array} {c} 5=-\ frac {1} {2} +b\\ \ frac {11} {2} =b \ end {array}\)	Resolver para\(\ b\).
\(\ y=-\frac{1}{2} x+\frac{11}{2}\)	Escribe la ecuación usando la nueva pendiente para\(\ m\) y la\(\ b\) que acabas de encontrar.

\ (\\ begin {array} {c} y=4\\ y=0 x+4 \ end {array}\)	Vuelva a escribir la línea en\(\ y=m x+b\) forma, si es necesario. Puede notar sin hacer esto que\(\ y=4\) es una línea horizontal 4 unidades por encima del eje x. Debido a que es horizontal, sabes que su pendiente es cero.
En la ecuación anterior,\(\ m=0\) y\(\ b=4\). Ya que\(\ m=0\), la pendiente es 0. Esta es una línea horizontal.	Identificar la pendiente de la línea dada.
La pendiente de la línea paralela también es 0.	Para encontrar la pendiente de una línea paralela, utilice la misma pendiente.
\(\ y=10\)	Dado que la línea paralela será una línea horizontal, su forma es\(\ y=a\) constante. Elija una constante para encontrar una línea paralela.
\(\ y=10\)	Esta línea es paralela\(\ y=4\) e interseca el eje y en\(\ (0,10)\).

Las líneas dadas están escritas en\(\ y=m x+b\) forma, con\(\ m=6\) para la primera línea y\(\ m=6\) para la segunda línea. La pendiente de ambas líneas es de 6.	Identificar las pendientes de las líneas dadas.
La primera línea tiene una intersección y en\(\ (0,5)\), y la segunda línea tiene una intersección en y en\(\ (0,-1)\). No son la misma línea.	Mira\(\ b\), el valor y de la intersección y, para ver si las líneas son quizás exactamente la misma línea, en cuyo caso no decimos que sean paralelas.
Las líneas son paralelas.	Las pendientes de las líneas son las mismas y tienen diferentes intercepciones y, por lo tanto, no son la misma línea y son paralelas.

\ (\\ comenzar {alineado} x-y &=\\\\\\\\\\\ 5\ -y &=-x+5\\ y &=\\\ x -5 \ final {alineado}\)	Reescribe la línea a la que quieres que sea paralela en el\(\ y=m x+b\) formulario, si es necesario.
En la ecuación anterior,\(\ m=1\) y\(\ b=-5\). Ya que\(\ m=1\), la pendiente es 1.	Identificar la pendiente de la línea dada.
La pendiente de la línea paralela es 1.	Para encontrar la pendiente de una línea paralela, utilice la misma pendiente.
\ (\\ begin {array} {c} y=m x+b\\ 1=1 (-2) +b \ end {array}\)	Utilice el método para escribir una ecuación a partir de la pendiente y un punto en la línea. Sustituir 1 por\(\ m\), y el punto\(\ (-2,1)\) por\(\ x\) y\(\ y\).
\ (\\ begin {array} {c} 1=-2+b\ \ quad 3=b \ end {array}\)	Resolver para\(\ b\).
\(\ y=x+3\)	Escribe la ecuación usando la nueva pendiente para\(\ m\) y la\(\ b\) que acabas de encontrar.