13.2.2: Escribir la ecuación de una línea

Objetivos de aprendizaje

• Encuentra la pendiente y la intercepción y, y escribe una ecuación de la línea.
• Dada la pendiente y un punto en la línea, escribir una ecuación de la línea.
• Dados dos puntos, escribir la ecuación de una línea.

Introducción

El concepto de pendiente es importante de entender porque a menudo se utiliza para medir la velocidad a la que se están produciendo los cambios.

Forma de pendiente-intercepción

Una ecuación lineal se puede expresar en la forma\(\ y=m x+b\). En esta ecuación,\(\ x\) y\(\ y\) son coordenadas de un punto,\(\ m\) está la pendiente, y\(\ b\) es la coordenada y de la intercepción y. Debido a que esta ecuación describe una línea en términos de su pendiente y su intercepción y, esta ecuación se denomina la forma pendiente-intercepción. Cuando se trabaja con relaciones lineales, la forma pendiente-intercepción ayuda a traducir entre la gráfica de una línea y la ecuación de una línea.

Al cambiar el valor de\(\ m\) en una ecuación lineal, se cambia la pendiente de la línea. Si\(\ m\) es positivo, la línea se incline hacia arriba a medida que se mueve de izquierda a derecha. Si\(\ m\) es negativo, la línea se incline hacia abajo a medida que se mueve de izquierda a derecha. Si\(\ m\) es cero, la línea es horizontal.

Cuando\(\ m\) es positivo, a medida que\(\ m\) se hace más grande la pendiente ascendente de la línea se vuelve más pronunciada. Cuando el valor de\(\ m\) se acerca a cero, la pendiente ascendente se aplana.

Cuando\(\ m\) es negativo, a medida que el valor absoluto de\(\ m\) aumenta la pendiente descendente de la línea se vuelve más pronunciada. Cuando el valor absoluto de\(\ m\) se acerca a cero, la pendiente descendente se aplana.

Cambiar el valor de\(\ b\) (la intercepción y) en una ecuación lineal mueve la línea hacia arriba y hacia abajo en el plano de coordenadas. Una intercepción y positiva significa que la línea cruza el eje y por encima del origen. Cuanto mayor sea el valor de\(\ b\), más arriba cruza el eje y. Una intercepción y negativa significa que la línea cruza por debajo del origen. Cuanto mayor sea el valor absoluto de\(\ b\), más abajo cruza el eje y.

Simplemente cambiando los valores de\(\ m\) y\(\ b\) en una ecuación lineal, puede definir cualquier línea. Así de poderosa y versátil es la fórmula pendiente-intercepción.

Actividad interactiva suplementaria

El siguiente gráfico representa cualquier línea que se pueda escribir en forma de pendiente-intercepción. Cuenta con dos barras deslizantes que pueden ser manipuladas. La barra etiquetada\(\ m\) permite ajustar la pendiente, o inclinación, de la línea. La barra etiquetada\(\ b\) cambia la intercepción y. Intente deslizar cada barra hacia adelante y hacia atrás, y vea cómo eso afecta a la línea.

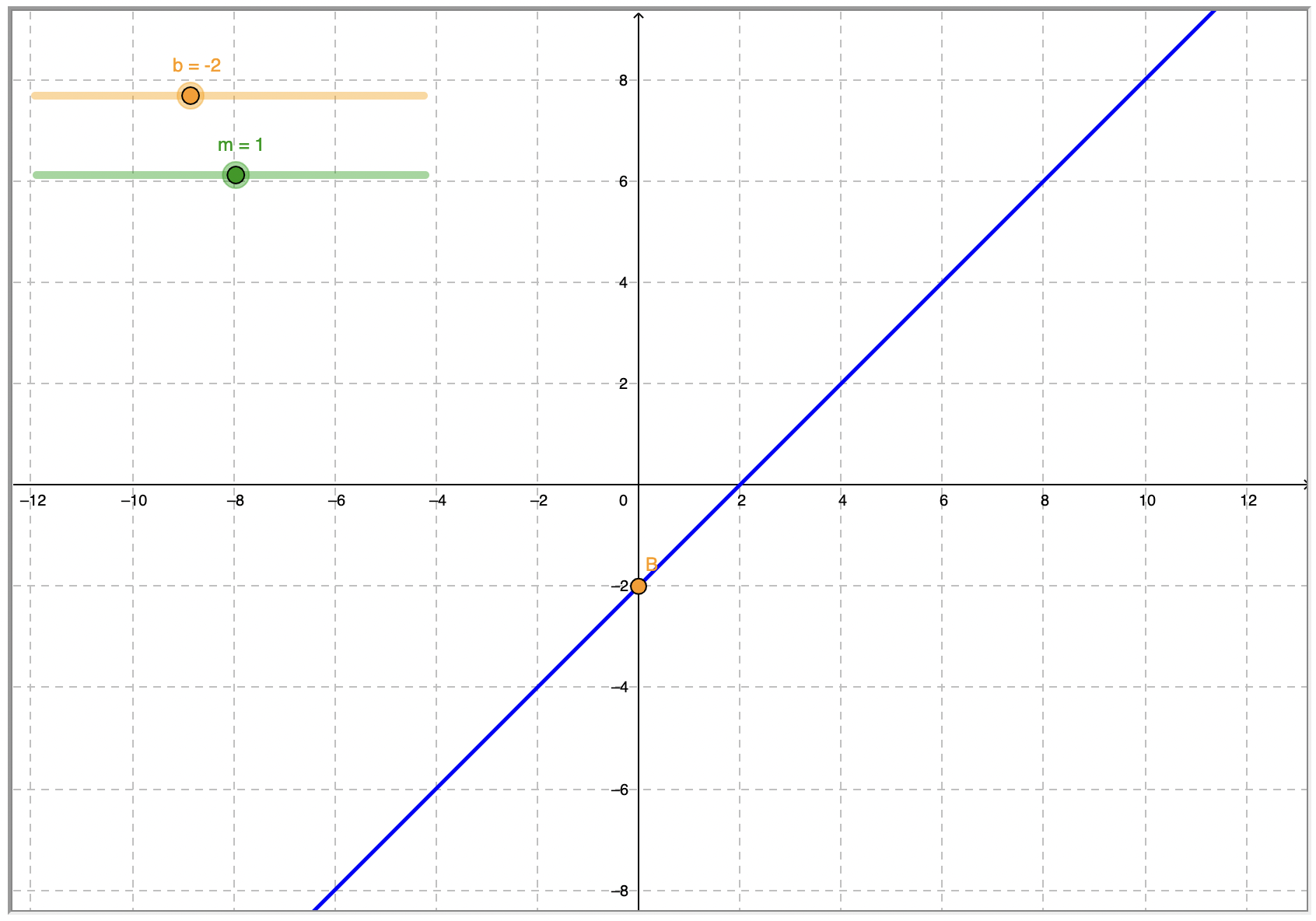
Ahora que entiendes la forma pendiente-intercepción, puedes mirar la gráfica de una línea y escribir su ecuación simplemente identificando la pendiente y la intercepción y de la gráfica. Vamos a probarlo con la línea en esta gráfica.

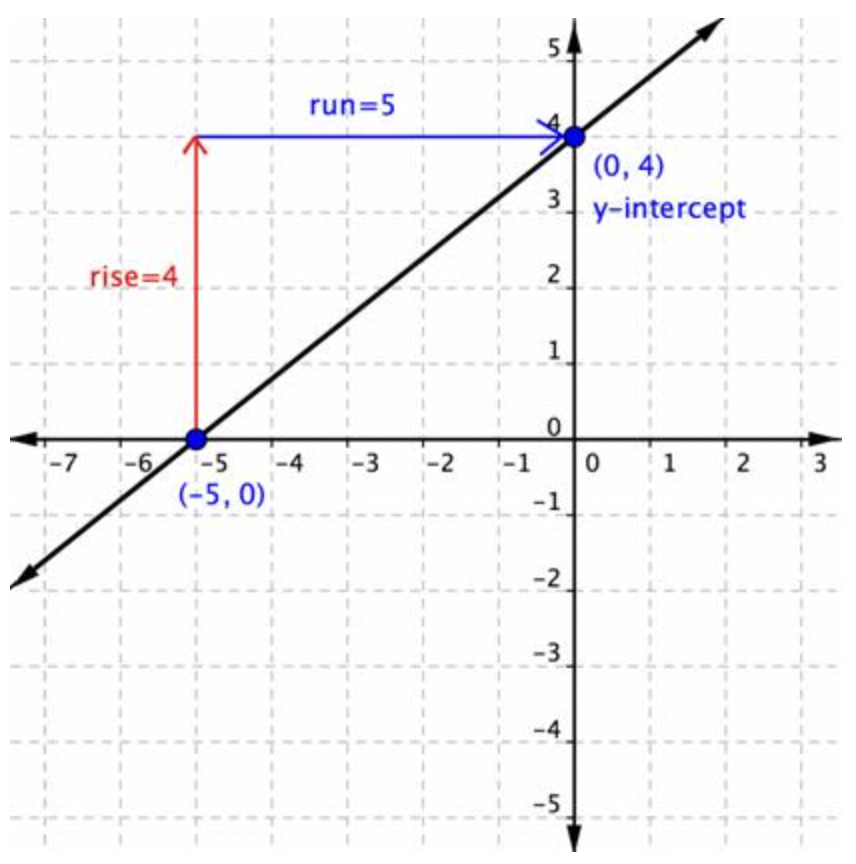
Para esta línea, la pendiente es\(\ \frac{4}{5}\), y la intercepción y es 4. Si pones esos valores en la forma pendiente-intercepción,\(\ y=m x+b\), obtienes la ecuación\(\ y=\frac{4}{5} x+4\).

Ejemplo

Escribe la ecuación de la línea que tiene una pendiente de\(\ \frac{1}{2}\) y una intercepción y de -5.

Solución

\(\ y=\frac{1}{2} x+b\)	Sustituya el talud (\(\ m\)) en\(\ y=m x+b\).
\(\ y=\frac{1}{2} x+(-5)\)o\(\ y=\frac{1}{2}-5\)	Sustituya la intercepción y\(\ (b)\) en la ecuación.

Si conoces la pendiente de una línea y un punto en la línea, puedes dibujar una gráfica. Entonces, usando una ecuación en la forma de punto-pendiente, puede identificar fácilmente la pendiente y un punto. Considera la ecuación\(\ y=-3 x-1\). Se puede decir a partir de esta ecuación que la intercepción y está en (0, -1). Comience trazando ese punto, (0, -1), en una gráfica.

También se puede decir por la ecuación que la pendiente de esta línea es -3. Así que empieza en (0, -1) y cuenta hasta 3 y más -1 (1 unidad en la dirección negativa, izquierda) y traza un segundo punto. (También podrías haber bajado 3 y más de 1.) Después dibuja una línea a través de ambos puntos, y ahí está, la gráfica de\(\ y=-3 x-1\).

Ejercicio

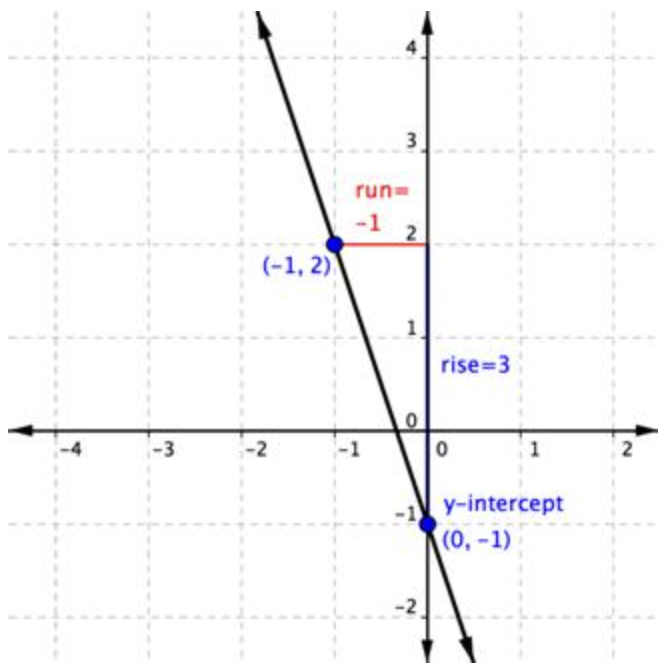
¿Cuál es la ecuación de una línea que tiene una pendiente de -2 y pasa por el punto (0, 8)?

1. \(\ y=-2 x+8\)
2. \(\ y=8 x-2\)
3. \(\ y=-2 x+0\)
4. \(\ 0=8 x-2\)

Contestar

1. Correcto. El punto (0, 8) es también la intercepción y de la línea, entonces\(\ b=8\). El desnivel,\(\ m\), es -2. Sustituyendo estos valores en la ecuación\(\ y=m x+b\), se encuentra\(\ y=-2 x+8\).
2. Incorrecto. Recuerde que en la forma pendiente-intercepción de una ecuación,\(\ y=m x+b\),\(\ m=\text { slope }\) y\(\ b=\) el valor y de la intercepción y. La elección correcta es\(\ y=-2 x+8\).
3. Incorrecto. Recuerda que en la forma pendiente-intercepción de una ecuación,\(\ y=m x+b\),\(\ b=\) el valor y (¡no el valor x!) de la intercepción y. La elección correcta es\(\ y=-2 x+8\).
4. Incorrecto. Recuerde que en la forma pendiente-intercepción de una ecuación,\(\ y=m x+b\),\(\ m=\) pendiente y\(\ b=\) el valor y de la intercepción y. La elección correcta es\(\ y=-2 x+8\).

Pendiente y un punto en la línea

El uso de la forma pendiente-intercepción para ayudar a escribir la ecuación de una línea es posible cuando se conoce tanto la pendiente como la intercepción\(\ (m)\) y\(\ (b)\), pero ¿y si conoce la pendiente y cualquier punto de la línea, no específicamente la intercepción y? ¿Aún puedes escribir la ecuación? La respuesta es sí, pero tendrás que pensar y trabajar un poco más de lo que hacías antes.

Recordemos que un punto es un par de\(\ (x, y)\) coordenadas y que todos los puntos de la línea satisfarán la ecuación lineal. Entonces, si tienes un punto en la línea, debe ser una solución a la ecuación. Aunque todavía no conoces la ecuación exacta, sabes que puedes expresar la línea en forma de pendiente-intercepción,\(\ y=m x+b\).

Conoces la pendiente\(\ (m)\), pero simplemente no conoces el valor de la intercepción y\(\ (b)\). Dado que el punto\(\ (x, y)\) es una solución a la ecuación, puedes sustituir sus coordenadas por\(\ x\) y\(\ y\) en\(\ y=m x+b\) y resolver para encontrar\(\ b\)!

Esto puede parecer un poco confuso con todas las variables, pero un ejemplo con una pendiente real y un punto ayudará a aclarar.

Ejemplo

Escribe la ecuación de la línea que tiene una pendiente de 3 y contiene el punto (1, 4).

Solución

\(\ y=3 x+b\)	Sustituir la pendiente\(\ (m)\) en\(\ y=m x+b\).
\(\ 4=3(1)+b\)	Sustituir el punto (1, 4) por\(\ x\) y\(\ y\).
\ (\\ begin {array} {c} 4=3+b\\ 1=b \ end {array}\)	Resolver para\(\ b\).
\(\ y=3 x+1\)	Reescribir\(\ y=m x+b\) con\(\ m=3\) y\(\ b=1\).

Para confirmar nuestro álgebra, puede verificar graficando la ecuación\(\ y=3 x+1\). La ecuación comprueba porque cuando se grafica, pasa por el punto (1, 4).

Ejemplo Avanzado

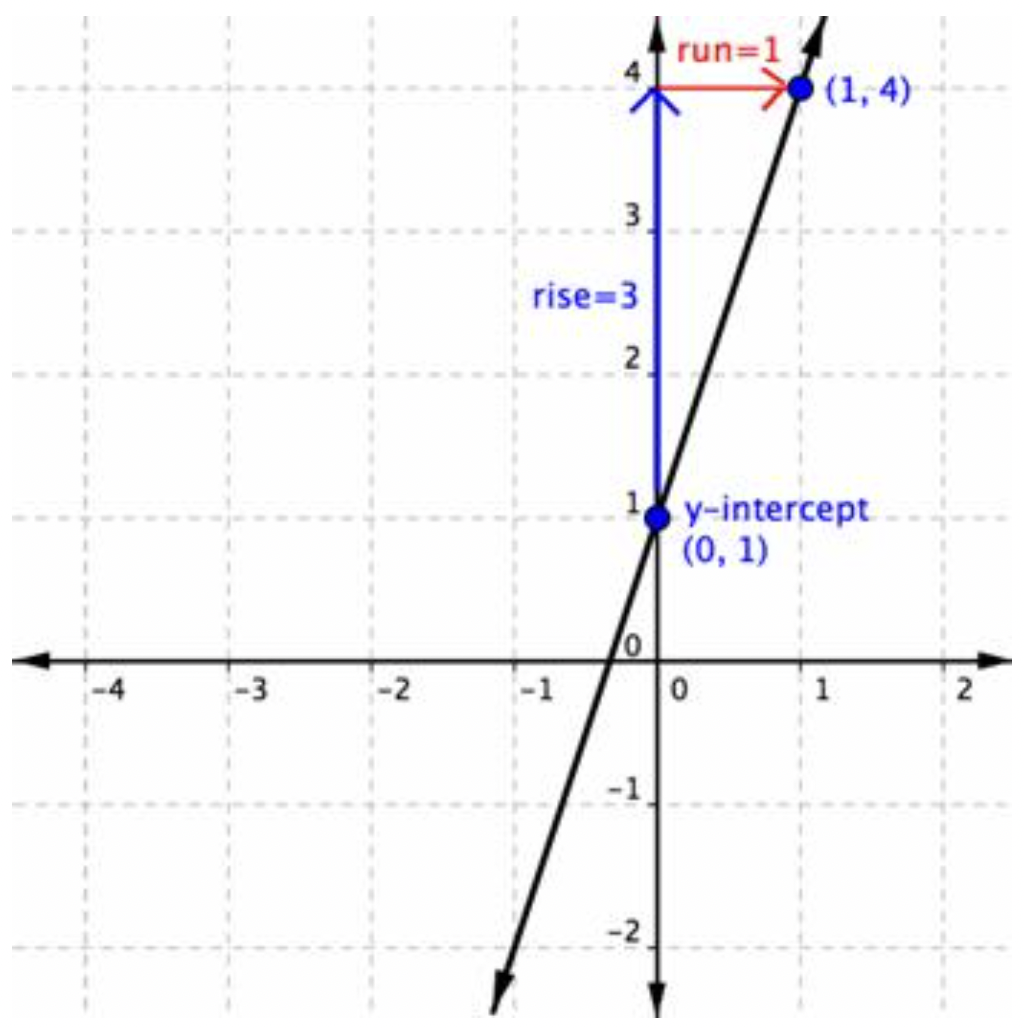
Escribe la ecuación de la línea que tiene una pendiente de\(\ -\frac{7}{8}\) y contiene el punto\(\ \left(4, \frac{5}{4}\right)\).

Solución

\ (\\ comenzar {alineado} y&=m x+b\ y&=-\ frac {7} {8} x+b \ final {alineado}\)	Sustituir la pendiente\(\ (m)\) en\(\ y=m x+b\).
\(\ \frac{5}{4}=-\frac{7}{8}(4)+b\)	Sustituir el punto\(\ \left(4, \frac{5}{4}\right)\) por\(\ x\) y\(\ y\).
\ (\\ begin {array} {r} \ frac {5} {4} =-\ frac {28} {8} +b\\ \ frac {5} {4} =-\ frac {14} {4} +b\ \ frac {5} {4} +\ frac {14} {4} =-\ frac {14} {4} +\ frac {14} {4} +b\\ \ frac {19} {4} =b \ end {array}\)	Resolver para\(\ b\).
\(\ y=-\frac{7}{8} x+\frac{19}{4}\)	Reescribir\(\ y=m x+b\) con\(\ m=-\frac{7}{8}\) y\(\ b=\frac{19}{4}\).

Ejercicio

Escribe la forma pendiente-intercepción de la línea con una pendiente de\(\ \frac{2}{3}\) y que contiene el punto\(\ (9,4)\).

1. \(\ y=-2 x+\frac{2}{3}\)
2. \(\ y=\frac{2}{3} x-2\)
3. \(\ y=\frac{2}{3} x+10\)
4. \(\ y=\frac{2}{3} x+\frac{19}{3}\)

Contestar

1. Incorrecto. Resolviste correctamente para la intercepción y pero has usado la pendiente para la intercepción y y la intercepción para la pendiente cuando vuelves a enchufar\(\ y=m x+b\). La respuesta correcta es\(\ y=\frac{2}{3} x-2\).
2. Correcto. La pendiente de esta línea es\(\ \frac{2}{3}\) y la intercepción y es -2.
3. Incorrecto. Revisa tu álgebra cuando lo resolviste para\(\ b\). Para encontrar\(\ b\), sustituir los valores conocidos por\(\ x\)\(\ y\), y\(\ m\) en la forma pendiente-intercepción. Esto te da\(\ 4=\frac{2}{3}(9)+b\), lo que simplifica a\(\ 4=6+b\), así\(\ b=-2\). La respuesta correcta es\(\ y=\frac{2}{3} x-2\).
4. Incorrecto. Al resolver for\(\ b\), utilizó el 9 como la coordenada y y 4 como la coordenada x. Para encontrar\(\ b\), sustituir los valores conocidos por\(\ x\)\(\ y\), y\(\ m\) en la forma pendiente-intercepción. Esto te da\(\ 4=\frac{2}{3}(9)+b\), lo que simplifica a\(\ 4=6+b\), así\(\ b=-2\). La respuesta correcta es\(\ y=\frac{2}{3} x-2\).

Pregunta Avanzada

Escribe la forma pendiente-intercepción de la línea con una pendiente de -0.6 y que contiene el punto (3.8, 7.25).

1. \(\ y=-0.6 x+3.8\)
2. \(\ y=-0.6 x+4.97\)
3. \(\ y=3.8 x+7.25\)
4. \(\ y=-0.6 x+9.53\)

Contestar

1. Incorrecto. El valor para\(\ m\) es correcto en esta ecuación, pero el valor para no lo\(\ b\) es. Trate de sustituir\(\ (3.8,7.25)\) en la ecuación\(\ y=-0.6 x+b\) y resolver para\(\ b\). La respuesta correcta es\(\ y=-0.6 x+9.53\).
2. Incorrecto. Parece que restaste\(\ 7.25-2.28\) para llegar a un\(\ b \text {-value }\) de 4.97. Vuelva a verificar los signos + y - en el problema. La respuesta correcta es\(\ y=-0.6 x+9.53\).
3. Incorrecto. El valor para\(\ m\) es incorrecto; recuerda que\(\ m\) representa la pendiente. La respuesta correcta es\(\ y=-0.6 x+9.53\).
4. Correcto. Sustituyendo\(\ (3.8,7.25)\) en la ecuación\(\ y=-0.6 x+b\), encontraste\(\ b=9.53\). Esto significa que la ecuación de la línea es\(\ y=-0.6 x+9.53\).

Dos puntos en la línea

Supongamos que no conoces ni la pendiente ni la intercepción en Y, pero sí conoces la ubicación de dos puntos en la línea. Es más desafiante, pero puedes encontrar la ecuación de la línea que pasaría por esos dos puntos. Volverá a utilizar el formulario de interceptación de pendiente para ayudarle.

La pendiente de una ecuación lineal es siempre la misma, independientemente de los dos puntos que utilice para encontrar la pendiente. Ya que tienes dos puntos, puedes usar esos puntos para encontrar la pendiente\(\ (m)\). ¡Ahora tienes la pendiente y un punto en la línea! Ahora puede sustituir valores por\(\ m\),\(\ x\), y\(\ y\) en la ecuación\(\ y=m x+b\) y encontrar\(\ b\).

Ejemplo

Escribe la ecuación de la línea que pasa por los puntos (2, 1) y (-1, -5).

Solución

\(\ \frac{1-(-5)}{2-(-1)}=\frac{6}{3}=2\)	Encuentra la pendiente usando los puntos dados.
\(\ y=2 x+b\)	Sustituir la pendiente\(\ (m)\) en\(\ y=m x+b\).
\(\ 1=2(2)+b\)	Sustituir las coordenadas de cualquiera de los puntos por\(\ x\) y\(\ y\) - utiliza este ejemplo\(\ (2,1)\).
\ (\\ comenzar {alineado} 1&=4+b\\ -3&=b \ end {alineado}\)	Resolver para\(\ b\).
\ (\\ begin {alineado} y&=2 x+ (-3),\ text {o}\\ y&=2 x-3 \ end {alineado}\)	Reescribir\(\ y=m x+b\) con\(\ m=2\) y\(\ b=-3\).

Observe que no importa qué punto use cuando sustituya y resuelva por\(\ b\) usted obtiene el mismo resultado de\(\ b\) cualquier manera. En el ejemplo anterior, sustituyó las coordenadas del punto\(\ (2,1)\) en la ecuación\(\ y=2 x+b\). Empecemos con la misma ecuación\(\ y=2 x+b\), pero sustituyamos en\(\ (-1,-5)\):

\ (\\ begin {alineado}
y&=2 x+b\\
-5&=2 (-1) +b\\
-5&=-2+b\\
-3&=b
\ end {alineado}\)

La ecuación final es la misma:\(\ y=2 x-3\).

Ejemplo Avanzado

Escribe la ecuación de la línea que pasa por los puntos\(\ (-4.6,6.45)\) y\(\ (1.15,7.6)\).

Solución

\(\ \frac{7.6-6.45}{1.15-(-4.6)}=\frac{1.15}{5.75}=0.2\)	Encuentra la pendiente usando los puntos dados.
\(\ y=0.2 x+b\)	Sustituir la pendiente\(\ (m)\) en\(\ y=m x+b\).
\ (\\ comenzar {alineado} 7.6 &=0.2 (1.15) +b\\ 7.6 &=0.23+b\\ 7.6-0.23 &=0.23-0.23+b\\ 7.37 &=b \ end {alineado}\)	Sustituir cualquiera de los puntos por\(\ x\) y\(\ y\). En este ejemplo se utiliza\(\ (1.15,7.6)\). Entonces resuelve para\(\ b\).
\(\ y=0.2 x+7.37\)	Reescribir\(\ y=m x+b\) con\(\ m=0.2\) y\(\ b=7.37\).

La ecuación de la línea que pasa por los puntos\(\ (-4.6,6.45)\) y\(\ (1.15,7.6)\) es\(\ y=0.2 x+7.37\).

Ejercicio

Escriba la forma pendiente-intercepción de la línea que pasa a través\(\ (5,2)\) y\(\ (-1,-10)\).

1. \(\ y=2 x+12\)
2. \(\ y=\frac{1}{2} x-\frac{7}{2}\)
3. \(\ y=2 x-8\)
4. \(\ y=2 x+1\)

Contestar

1. Incorrecto. La pendiente\(\ (m=2)\) es correcta, pero revisa tu álgebra cuando lo resolviste\(\ b\). Sustituir\(\ m=2\)\(\ x=5\),, y\(\ y=2\) en la ecuación\(\ y=m x+b\) para encontrar\(\ b\):\(\ 2=2(5)+b\), entonces\(\ 2=10+b\), así\(\ b=-8\). La respuesta correcta es\(\ y=2 x-8\).
2. Incorrecto. Parece que escribiste la pendiente como\(\ \frac{\text { run }}{\text { rise }}\) en vez de\(\ \frac{\text { rise }}{\text { run }}\). La respuesta correcta es\(\ y=2 x-8\).
3. Correcto. Encuentra la pendiente\(\ \frac{\text{rise}}{\text{run}}=\frac{-10-2}{-1-5}=\frac{-12}{-6}=2\). Después usa la pendiente y uno de los puntos para encontrar el valor de\(\ b\).
4. Incorrecto. Asegúrese de sustituir la coordenada x del punto por la\(\ x\) variable y la coordenada y por la\(\ y\) variable de\(\ y=m x+b\) al resolver para\(\ b\). La respuesta correcta es\(\ y=2 x-8\).

Pregunta Avanzada

¿Cuál de las siguientes líneas pasa por los puntos\(\ \left(\frac{3}{2},-4\right)\) y\(\ \left(\frac{7}{4},-2\right)\)?

1. \(\ y=\frac{1}{2} x-\frac{3}{4}\)
2. \(\ y=8 x-16\)
3. \(\ y=\frac{1}{2} x+16\)
4. \(\ y=8 x-\frac{3}{4}\)

Contestar

1. Incorrecto. Para encontrar la pendiente de la línea, usa la fórmula\(\ m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\). Después sustituya la pendiente en por\(\ m\) en la ecuación\(\ y=m x+b\) y resuelva para\(\ b\). La respuesta es\(\ y=8 x-16\).
2. Correcto. La pendiente de la línea sobre la que se encuentran estos puntos es 8, y sustituyendo cualquiera de los puntos en la ecuación\(\ y=8 x+b\) rinde\(\ b=-16\).
3. Incorrecto. Intente calcular de nuevo la pendiente usando la fórmula\(\ m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\). Cuando encuentres la pendiente, utilízala (y uno de los puntos dados) para encontrar el valor de\(\ b\). La respuesta correcta es\(\ y=8 x-16\).
4. Incorrecto. Has encontrado la pendiente correcta, pero el valor de\(\ b\) es incorrecto. Intente sustituir cualquiera\(\ \left(\frac{3}{2},-4\right)\) o\(\ \left(\frac{7}{4},-2\right)\) en la ecuación\(\ y=8 x+b\) para resolver\(\ b\). La respuesta correcta es\(\ y=8 x-16\).

Resumen

La forma pendiente-intercepción de una ecuación lineal se escribe como\(\ y=m x+b\), donde\(\ m\) está la pendiente y\(\ b\) es el valor de\(\ y\) en la intercepción y, que se puede escribir como\(\ (0, b)\). Cuando conoces la pendiente y la intercepción y de una línea, puedes usar la forma pendiente-intercepción para escribir inmediatamente la ecuación de esa línea. La forma pendiente-intercepción también puede ayudarte a escribir la ecuación de una línea cuando conoces la pendiente y un punto en la línea o cuando conoces dos puntos en la línea.