13.2.4: Graficar desigualdades lineales
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Determinar si un par ordenado es una solución a una desigualdad.
- Graficar una desigualdad en dos variables.
Introducción
Las desigualdades lineales se pueden graficar en un plano de coordenadas. Las soluciones para una desigualdad lineal están en una región del plano de coordenadas. Una línea límite, que es la ecuación lineal relacionada, sirve como límite para la región. Se puede utilizar una representación visual para averiguar qué valores hacen realidad la desigualdad y también cuáles la hacen falsa. Estudiemos las desigualdades volviendo al plano de coordenadas.
Desigualdades lineales como regiones
Las desigualdades lineales son diferentes a las ecuaciones lineales, aunque puedes aplicar lo que sabes sobre ecuaciones para ayudarte a entender las desigualdades. Las desigualdades y las ecuaciones son declaraciones matemáticas que comparan dos valores. Las ecuaciones utilizan el símbolo =; las desigualdades serán representadas por los símbolos <,≤,>, and ≥.
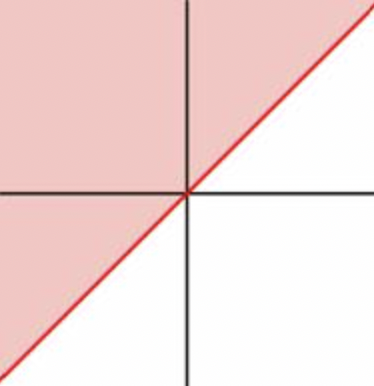
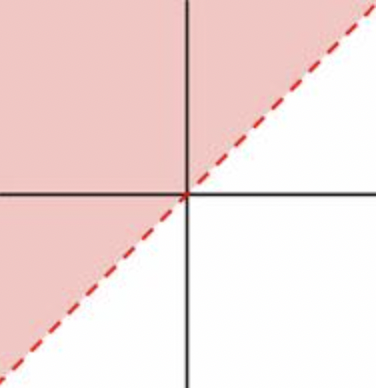
Una forma de visualizar las desigualdades de dos variables es trazarlas en un plano de coordenadas. Así es como x>y se ve la desigualdad. La solución es una región, que está sombreada.
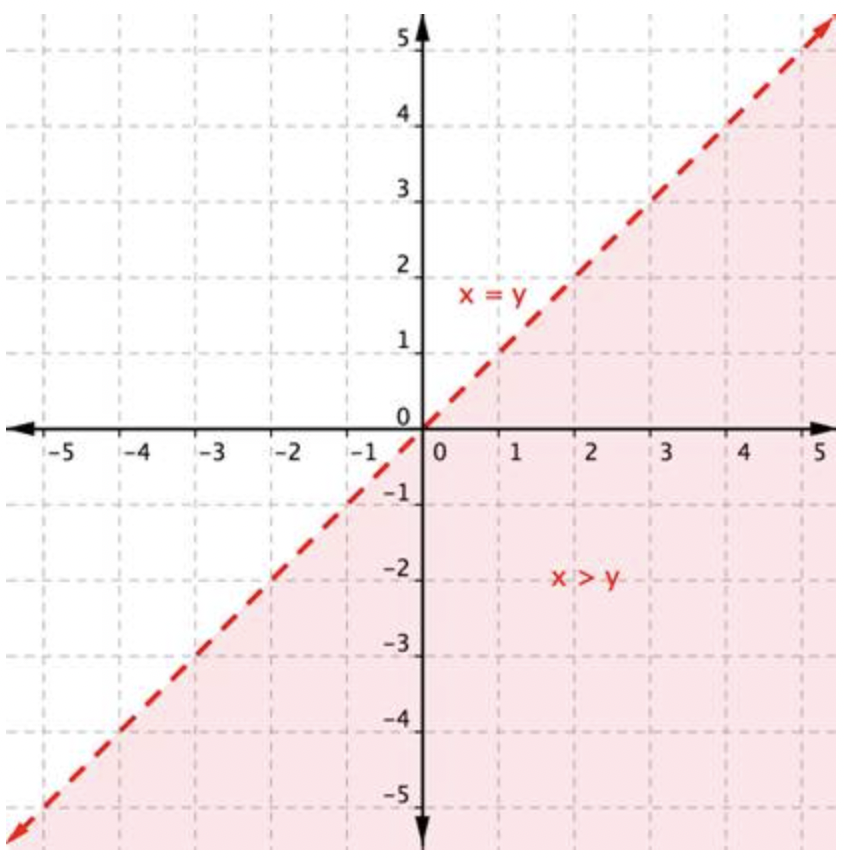
Aquí hay algunas cosas que entender. Primero, la línea límite roja discontinua es la gráfica de la ecuación lineal relacionada x=y. A continuación, la región de color rojo claro que está a la derecha de la línea (excluyendo la línea x=y) representa todo el conjunto de soluciones para la desigualdad x>y. ¿Recuerdas cómo todos los puntos de una línea son soluciones a la ecuación lineal de la línea? Bueno, todos los puntos de una región son soluciones a la desigualdad lineal que representa esa región.
Pensemos en ello por un momento, si x>y, entonces una gráfica de x>y mostrará todos los pares ordenados (x,y) para los cuales la coordenada x es mayor que la coordenada y.
La gráfica siguiente muestra la región así x>y como algunos pares ordenados en el plano de coordenadas. Mira cada par ordenado. ¿La coordenada x es mayor que la coordenada y? ¿El par ordenado se sienta dentro o fuera de la región sombreada?
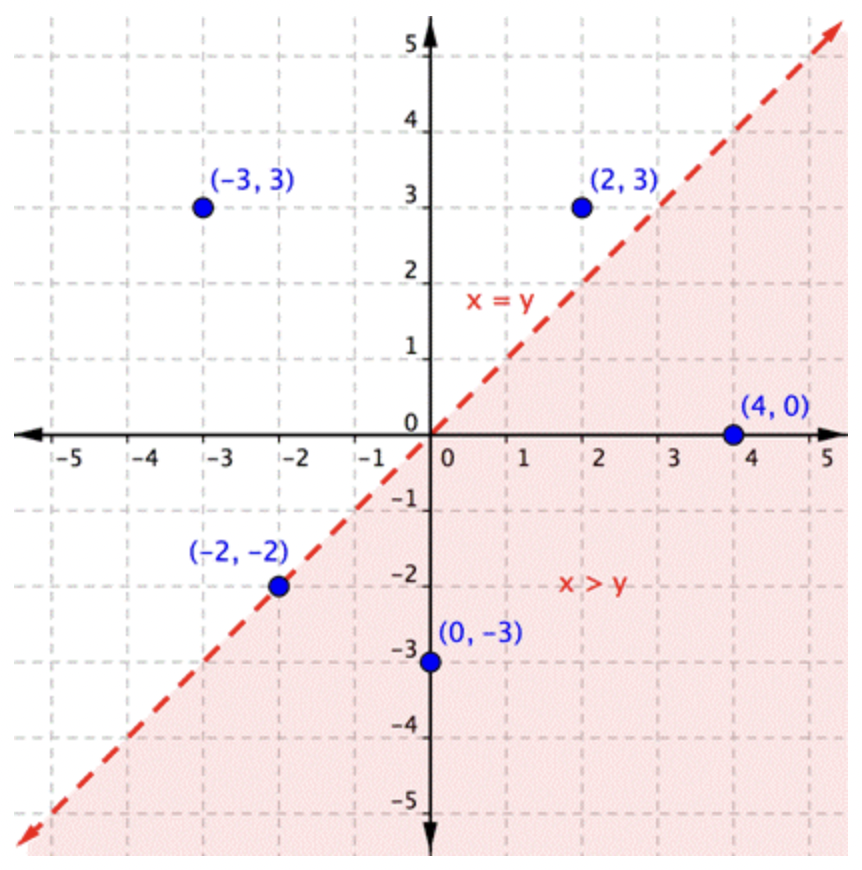
Los pares ordenados (4,0) y (0,−3) se encuentran dentro de la región sombreada. En estos pares ordenados, la coordenada x es mayor que la coordenada y. Estos pares ordenados están en el conjunto de solución de la ecuación x>y.
Los pares ordenados (−3,3) y (2,3) están fuera de la zona sombreada. En estos pares ordenados, la coordenada x es menor que la coordenada y, por lo tanto, no se incluyen en el conjunto de soluciones para la desigualdad.
El par ordenado (−2,−2) está en la línea límite. No es una solución ya que -2 no es mayor que -2. Sin embargo, si la desigualdad hubiera sido x≥y (leída como " xes mayor o igual a y “), entonces se (−2,−2) habría incluido (y la línea habría sido representada por una línea sólida, no una línea discontinua).
Echemos un vistazo a un ejemplo más: la desigualdad 3x+2y≤6. La gráfica siguiente muestra la región de valores que hace que esta desigualdad sea verdadera (sombreada en rojo), la línea límite 3x+2y=6, así como un puñado de pares ordenados. La línea límite es sólida esta vez, porque los puntos en la línea límite 3x+2y=6 harán que la desigualdad sea 3x+2y≤6 cierta.
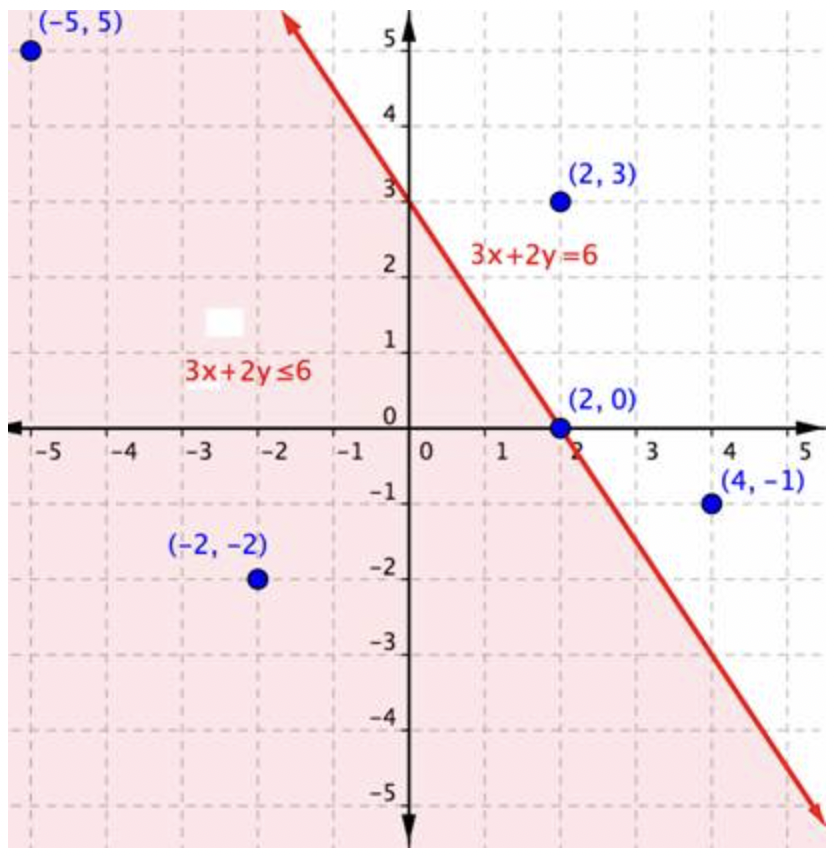
Como hiciste con el ejemplo anterior, puedes sustituir los valores x e y en cada uno de los pares (x,y) ordenados en la desigualdad para encontrar soluciones. Si bien es posible que hayas podido hacer esto en tu cabeza por la desigualdad x>y, a veces hacer una tabla de valores tiene sentido para desigualdades más complicadas.
| Par Pedido | Hace de la desigualdad 3x+2y≤6 una verdadera declaración | Hace de la desigualdad 3x+2y≤6 una declaración falsa |
| (−5,5) | \ (\\ begin {array} {c} 3 (-5) +2 (5)\ leq 6\\ -15+10\ leq 6\\ \ color {verde} -5\ leq 6 \ end {array}\) |
|
| (−2,−2) | \ (\\ begin {array} {c} 3 (-2) +2 (-2)\ leq 6\\ -6+ (-4)\ leq 6\\ \ color {verde} -10\ leq 6 \ end {array}\) |
|
| (2,3) | \ (\\ begin {array} {c} 3 (2) +2 (3)\ leq 6\\ 6+6\ leq 6\\ \ color {rojo} 12\ leq 6 \ end {array}\) |
|
| (2,0) | \ (\\ begin {array} {c} 3 (2) +2 (0)\ leq 6\\ 6+0\ leq 6\\ \ color {verde} 6\ leq 6 \ end {array}\) |
|
| (4,−1) | \ (\\ begin {array} {c} 3 (4) +2 (-1)\ leq 6\\ 12+ (-2)\ leq 6\\ \ color {rojo} 10\ leq 6 \ end {array}\) |
Si la sustitución (x,y) en la desigualdad produce una declaración verdadera, entonces el par ordenado es una solución a la desigualdad, y el punto se trazará dentro de la región sombreada o el punto será parte de una línea límite sólida. Una declaración falsa significa que el par ordenado no es una solución, y el punto se graficará fuera de la región sombreada, o el punto será parte de una línea límite punteada.
Utilice la gráfica para determinar qué pares ordenados trazados a continuación son soluciones de la desigualdad x−y<3.
Solución
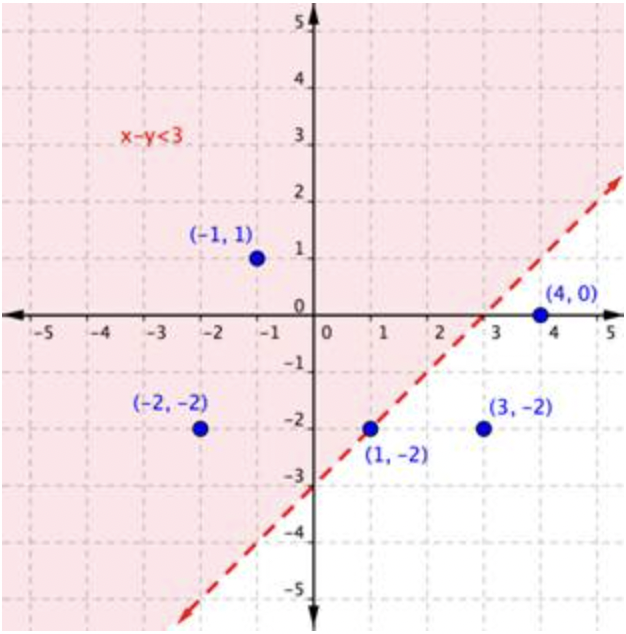
| Las soluciones se ubicarán en la región sombreada. Dado que se trata de un problema “menor que”, los pares ordenados en la línea límite no se incluyen en el conjunto de soluciones. | |
| \ (\\ begin {array} {r} (-1,1)\\ (-2, -2) \ end {array}\) |
Estos valores se encuentran en la región sombreada, también lo son las soluciones. (Cuando se sustituyen en la desigualdad x−y<3, producen declaraciones verdaderas.) |
| \ (\\ begin {array} {l} (1, -2)\\ (3, -2)\\ (4,0) \ end {array}\) |
Estos valores no se encuentran en la región sombreada, por lo que no son soluciones. (Cuando se sustituyen en la desigualdad x−y<3, producen declaraciones falsas.) |
\ (\\ begin {array} {c}
(-1,1),\\
(-2, -2)
\ end {array}\)
¿Es (2,−3) una solución de la desigualdad y<−3x+1?
Solución
| y<−3x+1 | Si (2,−3) es una solución, entonces producirá una declaración verdadera cuando se sustituya en la desigualdad y<−3x+1. |
| −3<−3(2)+1 | Sustituto x=2 y y=−3 en desigualdad. |
| −3<−6+1 | Evaluar. |
| −3<−5 | Esta afirmación no es cierta, por lo que el par ordenado no (2,−3) es una solución. |
(2,−3)no es una solución.
¿Qué par ordenado es una solución de la desigualdad 2y−5x<2?
- (−5,1)
- (−3,3)
- (1,5)
- (3,3)
- Contestar
-
- Incorrecto. Sustituyendo (−5,1) en 2y−5x<2, encuentras 2(1)−5(−5)<2, o no 2+25<2.27 es menor que 2, así que esto no puede ser correcto. La respuesta correcta es (3,3).
- Incorrecto. Sustituyendo (−3,3) en 2y−5x<2, encuentras 2(3)−5(−3)<2, o 6+15<2. 21 no es menor que 2, así que esto no puede ser correcto. La respuesta correcta es (3,3).
- Incorrecto. Sustituyendo (1,5) en 2y−5x<2, encuentras 2(5)−5(1)<2, o 10−5<2. 5 no es menor que 2, por lo que esto no puede ser correcto. La respuesta correcta es (3,3).
- Correcto. Sustituyendo (3,3) en 2y−5x<2, encuentras 2(3)−5(3)<2, o 6−15<2. Esta es una verdadera afirmación, por lo que es una solución a la desigualdad.
Graficando las Desigualdades
Entonces, ¿cómo se llega de la forma algebraica de una desigualdad, como y>3x+1, a una gráfica de esa desigualdad? Trazar desigualdades es bastante sencillo si sigues un par de pasos.
Para graficar una desigualdad:
- Grafique la línea límite relacionada. Reemplace el signo <, >, ≤ o ≥ en la desigualdad por = para encontrar la ecuación de la línea límite.
- Identificar al menos un par ordenado a cada lado de la línea límite y sustituir esos (x,y) valores en la desigualdad. Sombra la región que contiene los pares ordenados que hacen de la desigualdad una verdadera declaración.
- Si los puntos de la línea de límite son soluciones, utilice una línea sólida para dibujar la línea de límite. Esto sucederá para ≤ o ≥ desigualdades.
Vamos a graficar la desigualdad x+4y≤4
Para graficar la línea límite, busque al menos dos valores que se encuentren en la línea x+4y=4. Puede usar las intercepciones x e y para esta ecuación sustituyendo 0 in por x primero y encontrando el valor de y; luego sustituya 0 in por y y encuentre x.
| x | y |
| 0 | 1 |
| 4 | 0 |
Trace los puntos (0,1) y (4,0), y dibuje una línea a través de estos dos puntos para la línea de límite. La línea es sólida porque ≤ significa “menor que o igual a”, por lo que todos los pares ordenados a lo largo de la línea se incluyen en el conjunto de soluciones.
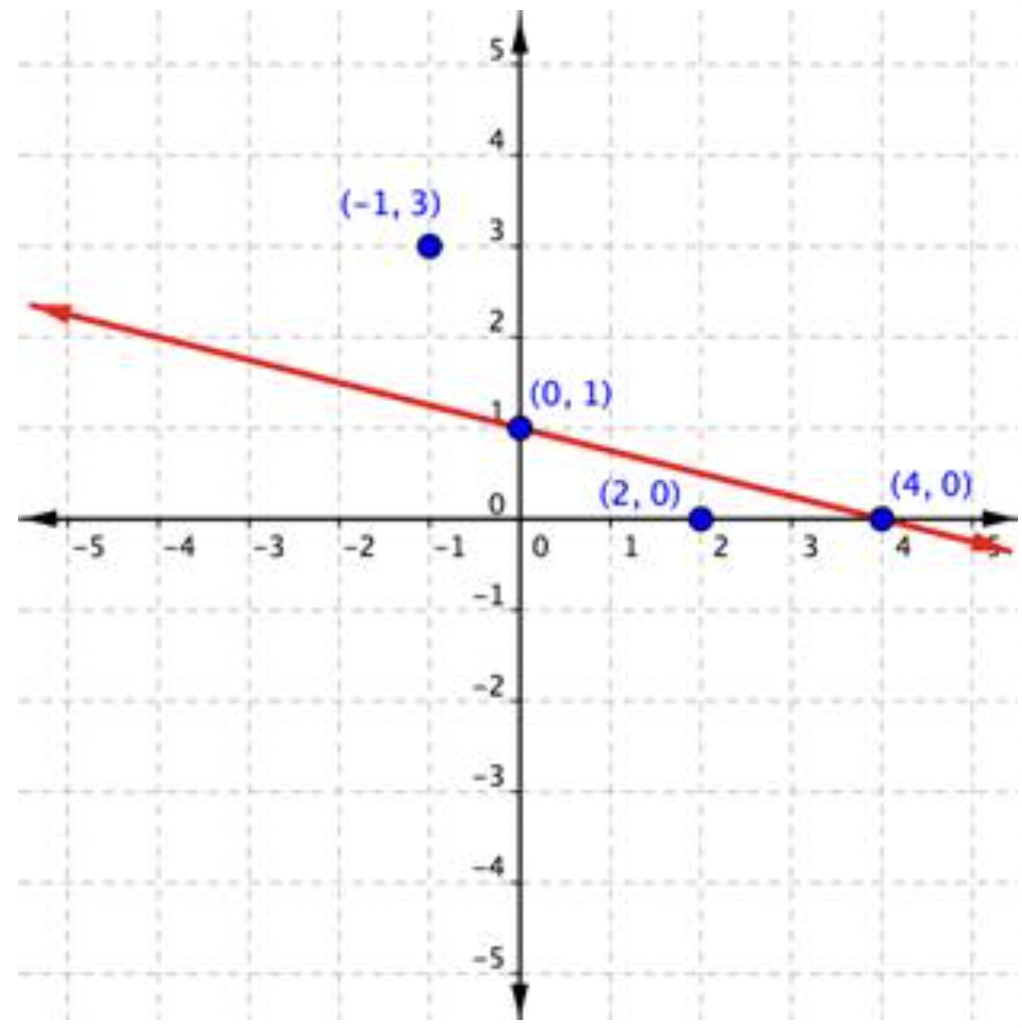
El siguiente paso es encontrar la región que contiene las soluciones. ¿Está por encima o por debajo de la línea límite? Para identificar la región donde la desigualdad es cierta, puede probar un par de pares ordenados, uno a cada lado de la línea límite.
Si sustituye (−1,3) en x+4y≤4:
\ (\\ begin {array} {r}
-1+4 (3)\ leq 4\\
-1+12\ leq 4\\
11\ leq 4
\ end {array}\)
Se trata de una declaración falsa, ya que 11 no es menor o igual a 4.
Por otro lado, si se sustituye (2,0) en x+4y≤4:
\ (\\ begin {array} {r}
2+4 (0)\ leq 4\\
2+0\ leq 4\\
2\ leq 4
\ end {array}\)
¡Esto es verdad! La región que incluye (2,0) debe estar sombreada, ya que esta es la región de soluciones.
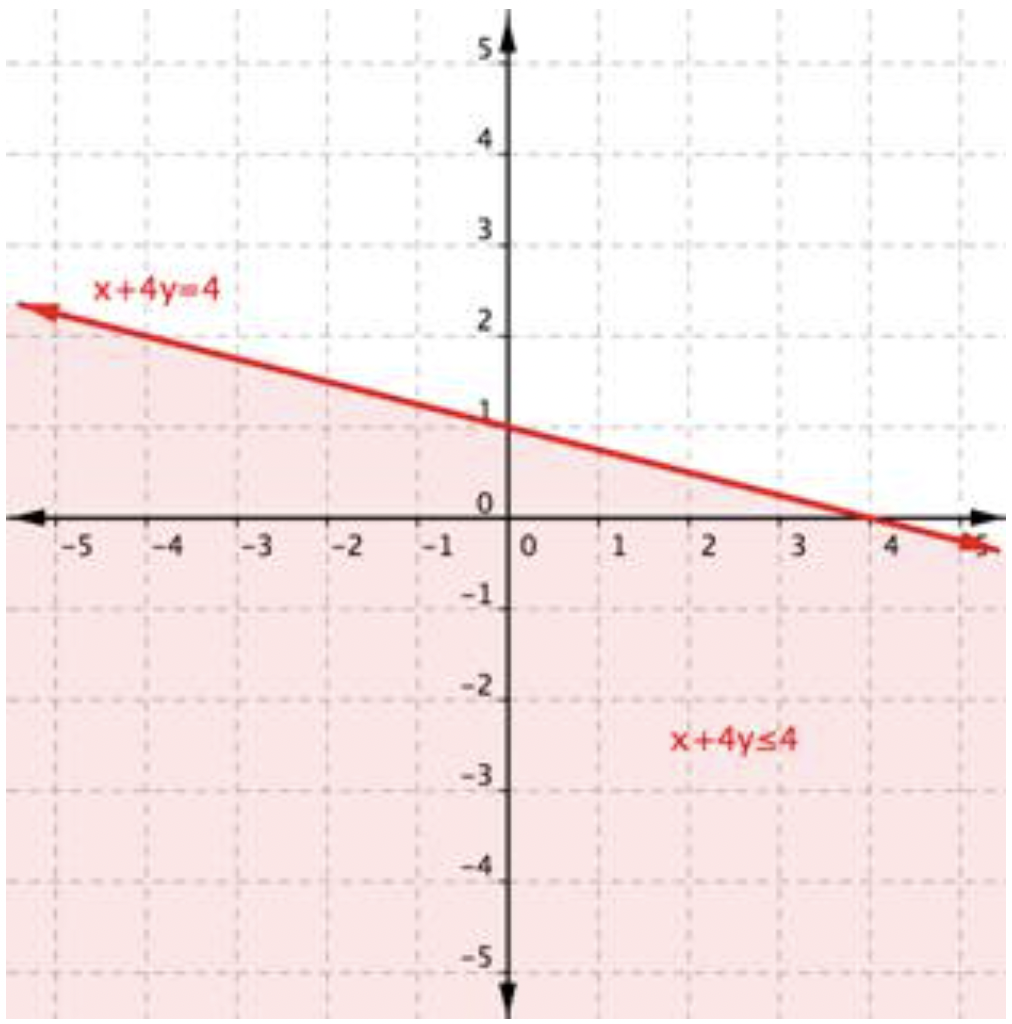
Y ahí lo tienes —la gráfica del conjunto de soluciones para x+4y≤4.
Grafica la desigualdad 2y>4x−6.
Solución
| \ (\\ begin {array} {l} 2 y>4 x-6\ \ frac {2 y} {x} >\ frac {4 x} {2} -\ frac {6} {2}\ y>2 x-3\ y=2 x-3 \ end {array}\) |
Resolver para y | ||||||
|
Cree una tabla de valores para encontrar dos puntos en la línea y=2x−3, o graficarla en base al método pendiente-intercepción, el b valor de la intercepción y es -3 y la pendiente es 2. | ||||||
| Trace los puntos y grafique la línea. La línea está punteada porque el signo en la desigualdad es >, no ≥ y por lo tanto los puntos en la línea no son soluciones a la desigualdad. | |||||||
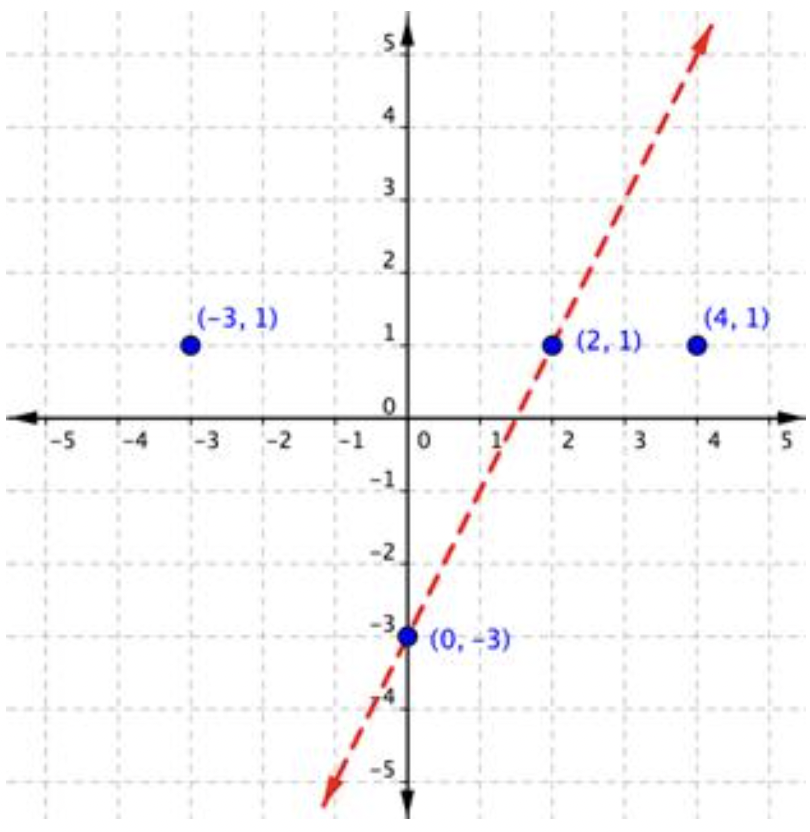 |
|||||||
| \ (\\ begin {array} {r} 2 y>4 x-6\ \ text {Prueba} 1 :( -3,1)\\ 2 (1) >4 (-3) -6\\ 2>-12-6\ \ color {verde} 2>-18\ text {¡Cierto! } \ end {array}\) |
Encuentra un par ordenado a cada lado de la línea de límite. Inserte los valores x e y en la desigualdad 2y>4x−6 y vea qué par ordenado da como resultado una declaración verdadera. | ||||||
| \ (\\ begin {array} {r} \ text {Test} 2 :( 4,1)\\ 2 (1) >4 (4) -6\\ 2>16-6\\ \ color {rojo} 2>10\ text {¡Falso! } \ end {array}\) |
Dado que (−3,1) resulta en una declaración verdadera, la región que incluye (−3,1) debe ser sombreada. |
La gráfica de la desigualdad 2y>4x−6 es:
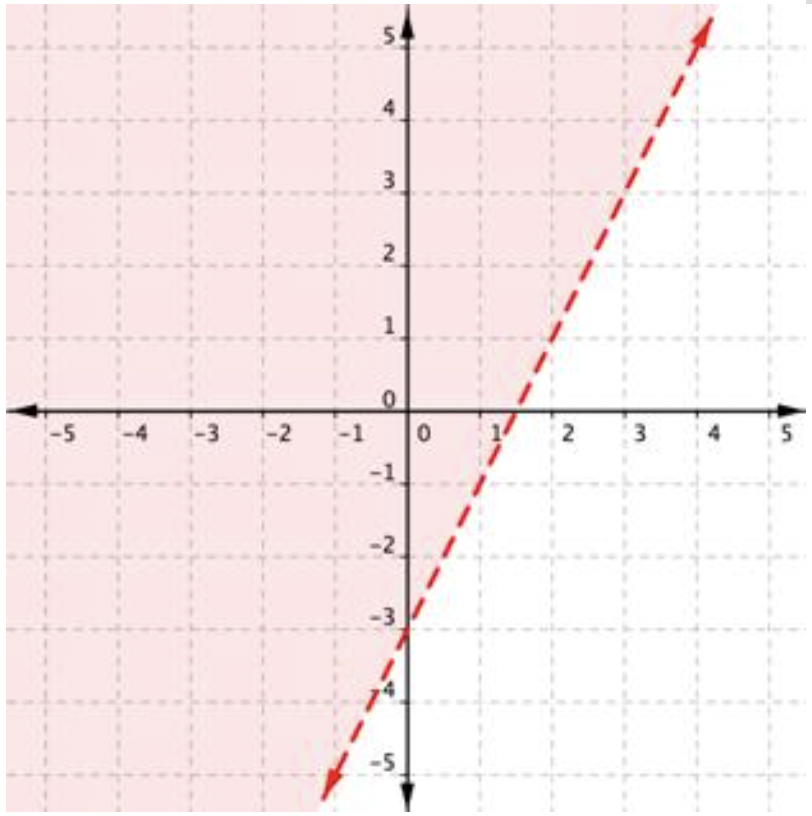
Una nota rápida sobre el problema anterior. Se pueden utilizar los puntos (0,−3) y (2,1) para graficar la línea de contorno, pero que estos puntos no se incluyen en la región de soluciones, ya que la región no incluye la línea límite!
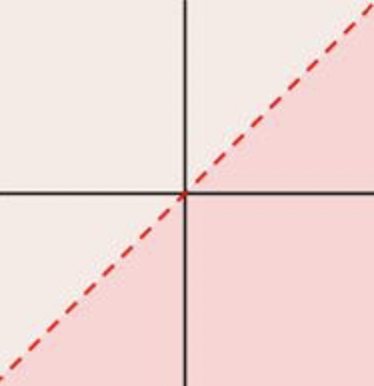
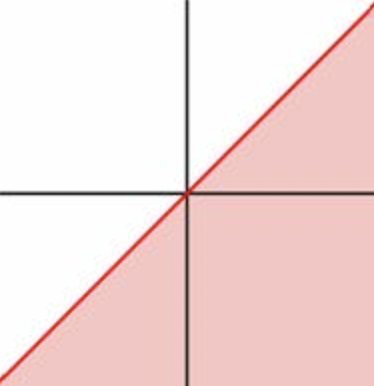
Cuando se traza en un plano de coordenadas, ¿cómo se y≥x ve la gráfica de?
- Contestar
-
Resumen
Cuando las desigualdades se grafican en un plano de coordenadas, las soluciones se ubican en una región del plano de coordenadas, que se representa como un área sombreada en el plano. La línea límite para la desigualdad se dibuja como una línea sólida si los puntos en la línea sí satisfacen la desigualdad, como en los casos de ≤ y ≥. Se dibuja como una línea discontinua si los puntos en la línea no satisfacen la desigualdad, como en los casos de < and >. Se puede decir a qué región sombrear probando algunos puntos en la desigualdad. El uso de un plano de coordenadas es especialmente útil para visualizar la región de soluciones para desigualdades con dos variables.