19.1.3: Trigonometría de Círculo Unitario
- Page ID
- 111212
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Entender círculo de unidad, ángulo de referencia, lado terminal, posición estándar.
- Encuentre los valores exactos de las funciones trigonométricas para los ángulos que miden\(30^{\circ}\)\(45^{\circ}\), y\(60^{\circ}\) usando el círculo unitario.
- Encuentre los valores exactos de la función trigonométrica de cualquier ángulo cuyo ángulo de referencia mida\(30^{\circ}\),\(45^{\circ}\), o\(60^{\circ}\).
- Determine los cuadrantes donde el seno, el coseno y la tangente son positivos y negativos.
Introducción
Los matemáticos crean definiciones porque tienen un uso en la solución de ciertos tipos de problemas. Por ejemplo, las seis funciones trigonométricas se definieron originalmente en términos de triángulos rectos porque eso fue útil para resolver problemas del mundo real que involucraban triángulos rectos, como encontrar ángulos de elevación. El dominio, o conjunto de valores de entrada, de estas funciones es el conjunto de ángulos entre\(0^{\circ}\) y\(90^{\circ}\). Ahora aprenderás nuevas definiciones para estas funciones en las que el dominio es el conjunto de todos los ángulos. Las nuevas funciones tendrán los mismos valores que las funciones originales cuando la entrada sea un ángulo agudo. En un triángulo rectángulo solo puedes tener ángulos agudos, pero verás la definición extendida para incluir otros ángulos.
Un uso de estas nuevas funciones es que se pueden usar para encontrar longitudes de lado y medidas de ángulo desconocidas en cualquier tipo de triángulo. Estas nuevas funciones se pueden utilizar en muchas situaciones que no tienen nada que ver con triángulos en absoluto.
Antes de mirar las nuevas definiciones, debe familiarizarse con la forma estándar en que los matemáticos dibujan y etiquetan ángulos.
Ángulos generales
A partir de la geometría, se sabe que un ángulo está formado por dos rayos. Los rayos se encuentran en un punto llamado vértice.
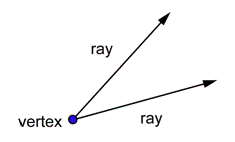
En trigonometría, los ángulos se colocan en ejes de coordenadas. El vértice siempre se coloca en el origen y un rayo siempre se coloca en el\(x\) eje positivo. A este rayo se le llama el lado inicial del ángulo. El otro rayo se llama el lado terminal del ángulo. Este posicionamiento de un ángulo se llama posición estándar. La letra griega theta (\(\theta\)) se utiliza a menudo para representar una medida de ángulo. A continuación se muestran dos ángulos en posición estándar.
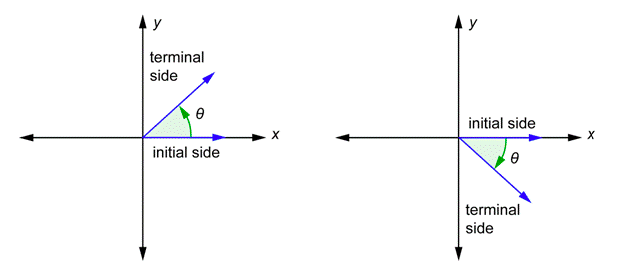
Cuando se dibuja un ángulo en posición estándar, tiene una dirección. Hay pequeñas flechas curvas en el dibujo anterior. El de la izquierda va en sentido antihorario y se define como un ángulo positivo. El de la derecha va en sentido horario y se define como un ángulo negativo. Si usaras un transportador para medir los ángulos, obtendrías\(50^{\circ}\) en ambos casos. Nos referimos al primero como\(50^{\circ}\) ángulo, y al segundo nos referimos como\(-50^{\circ}\) ángulo.
¿Por qué incluso tendrías ángulos negativos? Al igual que con todas las definiciones, es cuestión de conveniencia. Una nave espacial en órbita circular alrededor del ecuador terrestre podría estar viajando en cualquiera de dos direcciones. Entonces se podría decir que viajó por un\(-50^{\circ}\) ángulo para indicar que iba en dirección opuesta a una nave espacial que pasaba por un\(50^{\circ}\) ángulo. ¿Por qué es positivo en sentido antihorario? Esto es solo una convención, algo en lo que los matemáticos se han puesto de acuerdo, porque una forma tiene que ser positiva y la otra negativa.
Actividad Interactiva Suplementaria
Para entender cómo los ángulos positivos resultan de la rotación en sentido antihorario y los ángulos negativos resultan de la rotación en sentido horario, pruebe el ejercicio interactivo a continuación. Ingrese una medida de ángulo en el cuadro etiquetado Ángulo y golpee enter o use el control deslizante para mover el lado terminal del ángulo\(\theta\) a través de los cuadrantes.
*Insertar actividad interactiva
Problema: Dibuje un\(160^{\circ}\) ángulo en posición estándar.
Contestar
El ángulo es positivo, por lo que comienzas en el\(x\) eje -e irás en\(160^{\circ}\) sentido antihorario.
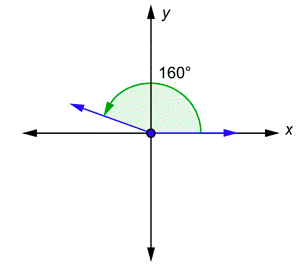
Problema: Dibuje un\(-200^{\circ}\) ángulo en posición estándar.
Contestar
El ángulo es negativo, por lo que comienzas en el\(x\) eje -y vas en\(200^{\circ}\) sentido horario. Recuerda que\(180^{\circ}\) es una línea recta. Eso te llevará al\(x\) eje negativo, y luego tienes que ir\(20^{\circ}\) más lejos.
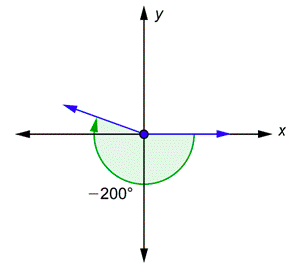
Observe que los lados terminales en los dos ejemplos anteriores son los mismos, pero representan ángulos diferentes. Se dice que tales pares de ángulos son ángulos coterminales.
Para cada ángulo dibujado en posición estándar, existe un ángulo relacionado conocido como ángulo de referencia. Este es el ángulo formado por el lado terminal y el\(x\) eje. El ángulo de referencia siempre se considera positivo, y tiene un valor en cualquier lugar de\(0^{\circ}\) a\(90^{\circ}\). A continuación se muestran dos ángulos en posición estándar.
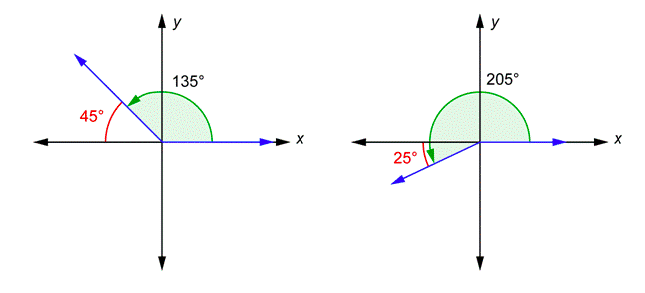
Se puede ver que el lado terminal del\(135^{\circ}\) ángulo y el\(x\) eje forman un\(45^{\circ}\) ángulo (esto se debe a que los dos ángulos deben sumar\(180^{\circ}\)). Este\(45^{\circ}\) ángulo, mostrado en rojo, es el ángulo de referencia para\(135^{\circ}\). El lado terminal del\(205^{\circ}\) ángulo y el\(x\) eje forman un\(25^{\circ}\) ángulo. Es\(25^{\circ}\) porque\(205^{\circ} = 180^{\circ} + 25^{\circ}\). Este\(25^{\circ}\) ángulo, mostrado en rojo, es el ángulo de referencia para\(205^{\circ}\).
Aquí hay dos ángulos más en posición estándar.
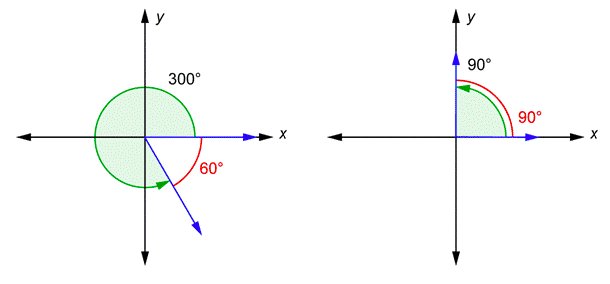
El lado terminal del\(300^{\circ}\) ángulo y el\(x\) eje forman un\(60^{\circ}\) ángulo (esto se debe a que los dos ángulos deben sumar\(360^{\circ}\)). Este\(60^{\circ}\) ángulo, mostrado en rojo, es el ángulo de referencia para\(300^{\circ}\). El lado terminal del\(90^{\circ}\) ángulo y el\(x\) eje forman un\(90^{\circ}\) ángulo. El ángulo de referencia es el mismo que el ángulo original en este caso. De hecho, cualquier ángulo de\(0^{\circ}\) a\(90^{\circ}\) es el mismo que su ángulo de referencia.
Problema: ¿Para qué sirve el ángulo de referencia\(100^{\circ}\)?
Contestar
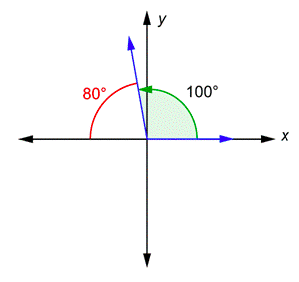
El lado terminal se encuentra en el Cuadrante II. El ángulo original y el ángulo de referencia forman juntos una línea recta a lo largo del\(x\) eje, por lo que su suma es\(180^{\circ}\).
Por lo tanto, el ángulo de referencia es\(80^{\circ}\).
El ángulo de referencia para\(180^{\circ}\) es\(80^{\circ}\).
Problema: ¿Para qué sirve el ángulo de referencia\(-70^{\circ}\)?
Contestar
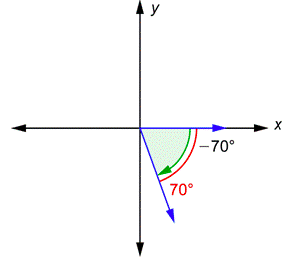
El lado terminal y el\(x\) eje forman el “mismo” ángulo que el original. Un ángulo de referencia es siempre un número positivo, por lo que el ángulo de referencia aquí es\(70^{\circ}\), mostrado en rojo.
El ángulo de referencia para\(-70^{\circ}\) es\(70^{\circ}\).
¿Para qué sirve el ángulo de referencia\(310^{\circ}\)?
- \(40^{\circ}\)
- \(50^{\circ}\)
- \(-40^{\circ}\)
- \(-50^{\circ}\)
- Contestar
-
- \(40^{\circ}\). Incorrecto. Es posible que hayas dibujado correctamente el ángulo en posición estándar, girando en sentido antihorario y aterrizando en el cuarto cuadrante. Sin embargo, es posible que haya mirado el ángulo formado por el lado terminal y el\(y\) eje -en lugar del\(x\) eje -eje. La respuesta correcta es\(50^{\circ}\).
- \(50^{\circ}\). Correcto. En posición estándar, el ángulo girará en sentido antihorario a través del primer, segundo, tercero y hacia el cuarto cuadrante. El ángulo de referencia y el ángulo original juntos forman un círculo completo, o\(360^{\circ}\). Por lo tanto, el ángulo de referencia es\(360^{\circ}-310^{\circ}=50^{\circ}\).
- \(-40^{\circ}\). Incorrecto. Es posible que hayas dibujado correctamente el ángulo en posición estándar, girando en sentido antihorario y aterrizando en el cuarto cuadrante. Sin embargo, es posible que haya mirado el ángulo formado por el lado terminal y el\(y\) eje -en lugar del\(x\) eje -eje. Además, el ángulo de referencia siempre es positivo. La respuesta correcta es\(50^{\circ}\).
- \(-50^{\circ}\). Incorrecto. Es posible que hayas dibujado correctamente el ángulo en posición estándar, girando en sentido antihorario y aterrizando en el cuarto cuadrante. Sin embargo, es posible que haya confundido el ángulo de referencia con un ángulo coterminal. Recuerda que el ángulo de referencia siempre es positivo. La respuesta correcta es\(50^{\circ}\).
Un círculo unitario es un círculo que está centrado en el origen y tiene un radio 1, como se muestra a continuación.
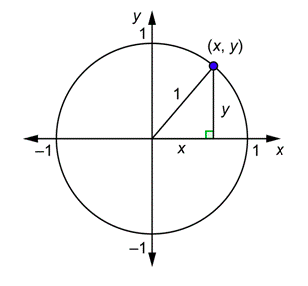
Si\((x,y)\) son las coordenadas de un punto en el círculo, entonces se puede ver desde el triángulo rectángulo en el dibujo y el Teorema de Pitágoras que\(x^2 + y^2 = 1\). Esta es la ecuación del círculo unitario.
La definición general de las funciones trigonométricas
El\(90^{\circ}\) triángulo\(30^{\circ}\)\(60^{\circ}\) - se ve abajo a la izquierda. Junto a eso hay un\(30^{\circ}\) ángulo dibujado en posición estándar junto con un círculo unitario.
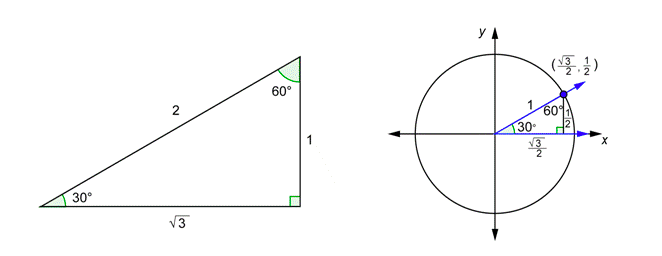
Los dos triángulos tienen los mismos ángulos, por lo que son similares. Por lo tanto, los lados correspondientes son proporcionales. La hipotenusa de la derecha tiene longitud 1 (porque es un radio). Dado que esta es la mitad de la hipotenusa de la izquierda, todos los lados de la derecha son la mitad de los lados correspondientes a la izquierda. Por ejemplo, el lado adyacente al\(30^{\circ}\) ángulo de la izquierda es\(\sqrt{3}\); por lo tanto, el lado correspondiente en el triángulo de la derecha tiene que ser la mitad de eso, o\(\frac{\sqrt{3}}{2}\).
Mira el triángulo derecho a la izquierda. Usando las definiciones de seno y coseno:
\(\cos 30^{\circ}=\frac{\sqrt{3}}{2} \text { and } \sin 30^{\circ}=\frac{1}{2}\)
Ahora mira el punto donde el lado terminal intersecta el círculo unitario. La\(x\) coordenada -es igual a\(\cos 30^{\circ}\), y la\(y\) coordenada -es igual a\(\sin 30^{\circ}\). Esto no es una coincidencia. Veamos un caso más general.
Supongamos que dibuja cualquier ángulo agudo\(\theta\) en posición estándar junto con un círculo unitario, como se ve a continuación.
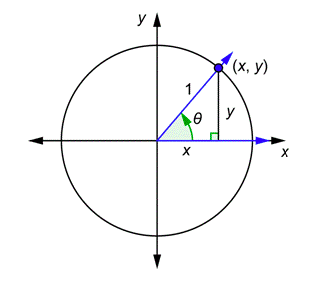
El lado terminal del ángulo intersecta el círculo unitario en el punto\((x,y)\). Escribamos las definiciones de las seis funciones trigonométricas y luego las reescribamos haciendo referencia al triángulo anterior y usando las variables\(x\) y\(y\).
\ (\ begin {array} {cc}
\ sin\ theta=\ frac {\ text {opuesto}} {\ text {hipotenusa}} =\ frac {y} {1} =y &\ csc\ theta=\ frac {\ text {hipotenusa}} {\ text {opuesto}} =\ frac {1} {y}\
\ cos\ theta=\ frac {\ texto {adyacente}} {\ texto {hipotenusa}} =\ frac {x} {1} =x &\ seg\ theta=\ frac {\ text { hipotenusa}} {\ texto {adyacente}} =\ frac {1} {x}\
\\ tan\ theta=\ frac {\ texto {opuesto}} {\ texto {adyacente}} =\ frac {y} {x} &\ cuna\ theta=\ frac {\ texto {adyacente}} {\ texto {opuesto}} =\ frac {x} {y} final
\ {matriz}\)
La primera ecuación y la de abajo, con los pasos medios recortados, te dicen:
\(\sin \theta=y \text { and } \cos \theta=x\)
Ahora se puede ver que la\(y\) coordenada -de este punto siempre es igual al seno del ángulo, y la\(x\) coordenada -de este punto siempre es igual al coseno del ángulo.
Ahora considere cualquier ángulo\(\theta\) en posición estándar junto con un círculo unitario. El lado terminal cruzará el círculo en algún momento\((x,y)\). Dependiendo del ángulo, ese punto podría estar en el primer, segundo, tercer o cuarto cuadrante.
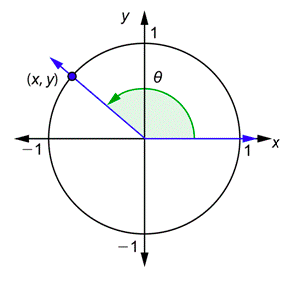
El seno del ángulo\(\theta\) es igual a la\(y\) coordenada -de este punto y el coseno del ángulo\(\theta\) es igual a la\(x\) coordenada -de este punto. De hecho, las seis funciones trigonométricas para cualquier ángulo ahora\(\theta\) están definidas por las seis ecuaciones enumeradas anteriormente.
Los siguientes ejemplos te ayudarán a confirmar que cuando\(\theta\) es un ángulo agudo, estas nuevas definiciones te dan los mismos resultados que las definiciones originales.
Problema: Dibuje un\(45^{\circ}\) ángulo en posición estándar junto con un círculo unitario. Confirme que las\(y\) coordenadas\(x\) - y -del punto de intersección del lado terminal y el círculo son iguales a\(\cos 45^{\circ}\) y\(\sin 45^{\circ}\).
Contestar
Comienza con el\(90^{\circ}\) triángulo\(45^{\circ}\)\(45^{\circ}\) - -. Después dibuja el\(45^{\circ}\) ángulo en posición estándar.
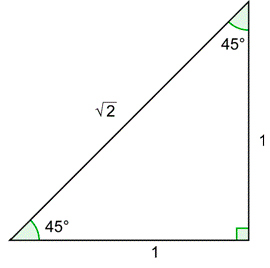
Este triángulo circular unitario es similar al\(90^{\circ}\) triángulo\(45^{\circ}\)\(45^{\circ}\) - -. Cada longitud de lado se puede obtener dividiendo las longitudes del\(90^{\circ}\) triángulo\(45^{\circ}\)\(45^{\circ}\) - por\(\sqrt{2}\). Entonces, cada pata en el triángulo del círculo unitario es:\(\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)
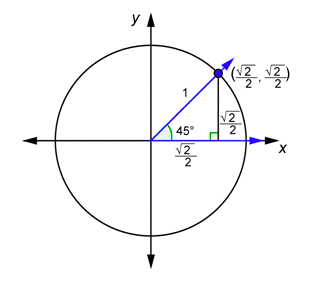
Mira las\(y\) coordenadas\(x\) - y -del punto en el círculo unitario, luego usa el triángulo para encontrar\(\cos 45^{\circ}\) y\(\sin 45^{\circ}\).
\ (\ begin {array} {l}
\ text {De las coordenadas en el}\\
\ text {círculo unitario:} x=\ frac {\ sqrt {2}} {2}
\ end {array}\)
\ (\ begin {array} {l}
\ text {Del triángulo:}\\
\ cos 45^ {\ circ} =\ frac {\ text {adyacente}} {\ text {hipotenusa}} =\ frac {1} {\ sqrt {2}} =\ frac {\ sqrt {2}} {2}} {2}
\ end {array}\)
\ (\ begin {array} {l}
\ text {De las coordenadas en el}\\
\ text {círculo unitario:} y=\ frac {\ sqrt {2}} {2}
\ end {array}\)
\ (\ begin {array} {l}
\ text {Del triángulo:}\\
\ sin 45^ {\ circ} =\ frac {\ text {opuesto}} {\ text {hipotenusa}} =\ frac {1} {\ sqrt {2}} =\ frac {\ sqrt {2}} {2}} {2}
\ end {array}\)
La\(x\) coordenada -es igual a\(\cos 45^{\circ}\), y la\(y\) coordenada -es igual a\(\sin 45^{\circ}\).
\(\text { Yes, } x=\cos 45^{\circ} \text { and } y=\sin 45^{\circ} \text { . }\)
En los siguientes dos ejemplos, las etiquetas angulares de\(37^{\circ}\) y\(53^{\circ}\) son en realidad aproximaciones muy cercanas. La idea principal de los ejemplos (que aquellas fracciones que involucran\(x\) y\(y\) son iguales a las diversas funciones trigonométricas) sigue siendo cierta.
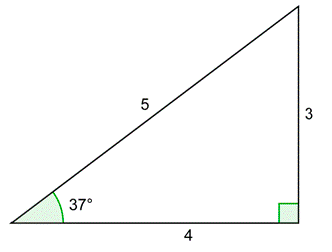
Problema: Dibuje un\(37^{\circ}\) ángulo en posición estándar junto con un círculo unitario. Usa el triángulo de abajo para encontrar las\(y\) coordenadas\(x\) - y -del punto de intersección del lado terminal y el círculo. Cómputos\(\frac{y}{x}\) y\(\frac{x}{y}\). Confirmar que son iguales a\(\tan 37^{\circ}\) y\(\cot 37^{\circ}\).
Contestar
Dibuja el\(37^{\circ}\) ángulo en posición estándar. El triángulo circular unitario es similar al triángulo rectángulo 3 - 4 - 5. Debido a que esta hipotenusa equivale a la hipotenusa original dividida por 5, puedes encontrar las longitudes de las piernas dividiendo las longitudes originales de las piernas por 5.
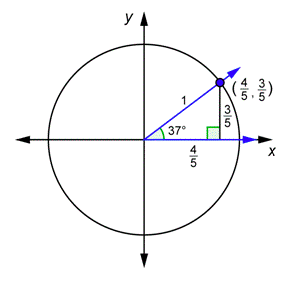
Encuentra las\(y\) coordenadas\(x\) - y -.
\(x=\frac{4}{5}, y=\frac{3}{5}\)
Compute las proporciones. Compara los resultados con lo que obtendrías\(\tan 37^{\circ}\) y\(\cot 37^{\circ}\) usando el triángulo original. ¡Ellos son lo mismo!
\ (\ begin {array} {l}
\ frac {y} {x} =\ frac {\ frac {3} {5}} {\ frac {4} {5}} =\ frac {3} {5}\ cdot\ frac {5} {4} =\ frac {3} {4}\
\ tan 37^ {\ circ} =\ frac {texto {opuesto}} {\ texto {adyacente}} =\ frac {3} {4}\
\ frac {x} {y} =\ frac {\ frac {4} {5}} {\ frac {3} {5}} =\ frac {4} {5}\ cdot\ frac {5} {3} =\ frac {4} {3} }\\
\ cuna 37^ {\ circ} =\ frac {\ texto {adyacente}} {\ texto {opuesto}} =\ frac {4} {3}
\ end {array}\)
\(\text { So yes, } \frac{y}{x}=\tan 37^{\circ} \text { and } \frac{x}{y}=\cot 37^{\circ}\)
Problema: Dibuje un\(53^{\circ}\) ángulo en posición estándar junto con un círculo unitario. Usa el triángulo de abajo para encontrar las\(y\) coordenadas\(x\) - y -del punto de intersección del lado terminal y el círculo. Cómputos\(\frac{1}{x}\) y\(\frac{1}{y}\). Confirmar que son iguales a\(\sec 53^{\circ}\) y\(\csc 53^{\circ}\).
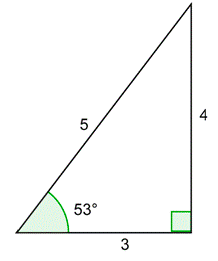
Contestar
Dibuja el\(53^{\circ}\) ángulo en posición estándar. El triángulo circular unitario es similar al triángulo rectángulo 3 - 4 - 5. Debido a que esta hipotenusa equivale a la hipotenusa original dividida por 5, puedes encontrar las longitudes de las piernas dividiendo las longitudes originales de las piernas por 5.
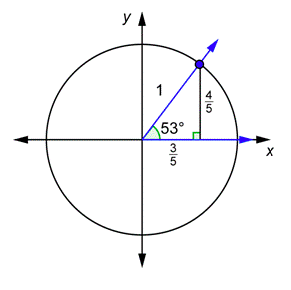
Encuentra las\(y\) coordenadas\(x\) - y -.
\(x=\frac{3}{5}, y=\frac{4}{5}\)
Compute las proporciones. Compara los resultados con lo que obtendrías\(\sec 53^{\circ}\) y\(\csc 53^{\circ}\) usando el triángulo original. ¡Ellos son lo mismo!
\(\text { Yes, } \frac{1}{x}=\sec 53^{\circ} \text { and } \frac{1}{y}=\csc 53^{\circ}\)
Las tres primeras de nuestras nuevas definiciones nos llevan a una identidad más importante:
\(\sin \theta=y, \cos \theta=x, \tan \theta=\frac{y}{x}\)
Podemos reemplazar\(y\) por\(\sin \theta\) y\(x\) por dentro\(\cos \theta\)\(\tan \theta = \frac{y}{x}\) para obtener la identidad de trigonometría\(\tan \theta = \frac{\sin \theta}{\cos \theta}\).
\(\tan \theta=\frac{y}{x}=\frac{\sin \theta}{\cos \theta}\)
Dado que la cotangente es el recíproco de la tangente, esto le da otra identidad trigonométrica.
\(\tan \theta=\frac{\sin \theta}{\cos \theta} \text { and } \cot \theta=\frac{\cos \theta}{\sin \theta}\)
Recuerde, una identidad es verdadera para cada valor posible de la variable. Entonces, no importa qué ángulo estés usando, los valores de tangente y cotangente están dados por estos cocientes.
Si bien algunos libros de texto dan definiciones generales ligeramente diferentes de las funciones trigonométricas, lo importante que hay que saber es que terminan dándote los mismos valores que las definiciones ya dadas a ti.
Por ejemplo, comience con un círculo de radio\(r\) (en lugar del radio 1) y un ángulo\(\theta\) en posición estándar. El lado terminal cruzará el círculo en algún momento\((x,y)\). Ese punto podría estar en cualquier cuadrante, pero mostramos uno en el primer cuadrante.
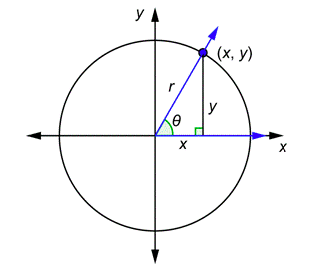
Ahora escribe las definiciones originales y luego vuelve a escribirlas usando las variables\(x\),\(y\), y\(r\).
\ (\ begin {array} {lr}
\ sin\ theta=\ frac {\ text {opuesto}} {\ texto {hipotenusa}} =\ frac {y} {r} &\ csc\ theta=\ frac {\ text {hipotenusa}} {\ text {opuesto}} =\ frac {r} {y}\\
\ cos\ theta=\ frac {\ texto {adyacente}} {\ texto {hipotenusa}} =\ frac {x} {r} &\ seg\ theta=\ frac {\ text { hipotenusa}} {\ texto {adyacente}} =\ frac {r} {x}\
\\ tan\ theta=\ frac {\ texto {opuesto}} {\ texto {adyacente}} =\ frac {y} {x} &\ cuna\ theta=\ frac {\ texto {adyacente}} {\ texto {opuesto}} =\ frac {x} {y} final
\ {matriz}\)
Estas seis fracciones se utilizan como definiciones generales de las funciones trigonométricas para cualquier ángulo\(\theta\), en cualquier cuadrante.
Problema: Calcular\(\frac{y}{x}\) usando el diagrama de abajo. Confirmar que esto es lo mismo que el valor de\(\tan 30^{\circ}\).
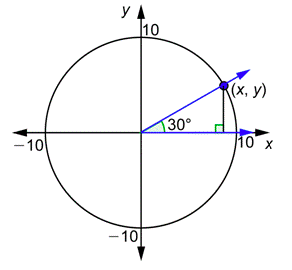
Contestar
El diagrama anterior contiene un\(90^{\circ}\) triángulo\(30^{\circ}\)\(60^{\circ}\) - -.
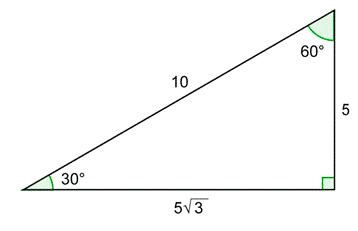
La hipotenusa es igual al radio, por lo que es de 10. El lado opuesto\(30^{\circ}\) es la mitad de 10, o 5. El lado adyacente es\(\sqrt{3}\) veces el lado opuesto, o\(5\sqrt{3}\).
Los lados del triángulo te dan los valores de\(x\) y\(y\) en el primer diagrama.
\ (\ begin {array} {c}
y=5\\
x=5\ sqrt {3}
\ end {array}\)
Sustituir estos en la definición.
\(\tan \theta=\frac{y}{x}=\frac{5}{5 \sqrt{3}}=\frac{5}{5 \sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{5 \sqrt{3}}{5 \cdot 3}=\frac{\sqrt{3}}{3}\)
Aquí está nuestro estándar\(30^{\circ}\) -\(60^{\circ}\) -\(90^{\circ}\) triángulo.
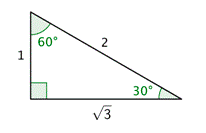
Calcular\(\tan 30^{\circ}\) usando la definición del triángulo rectángulo.
\ tan 30^ {\ circ} =\ frac {\ texto {opuesto}} {\ texto {adyacente}} =\ frac {1} {\ sqrt {3}} =\ frac {1} {\ sqrt {3}}\ cdot\ frac {\ sqrt {3}} {\ sqrt {3}} =\ frac {\ sqrt {3}}
\(\text { So yes, } \frac{y}{x}=\frac{\sqrt{3}}{3}=\tan 30^{\circ}\)
Uso de las Definiciones Generales de las Funciones Trigonométricas
Se le han dado definiciones nuevas o “generales” de las seis funciones trigonométricas y han visto que, cuando computas estas funciones usando ángulos agudos, el resultado es el mismo que el resultado que obtendrías al usar las definiciones originales. Ahora aprenderás a aplicar estas definiciones a ángulos que no son agudos y a ángulos negativos.
Dado cualquier ángulo\(\theta\), dibuje en posición estándar junto con un círculo unitario. El lado terminal cruzará el círculo en algún punto (\(x,y\)), como se muestra a continuación.
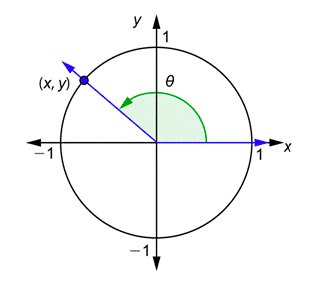
Aquí nuevamente están las definiciones generales de las seis funciones trigonométricas utilizando un círculo unitario.
| \(\sin \theta = y\) | \(\csc \theta = \frac{1}{y}\) |
| \(\cos \theta = x\) | \(\sec \theta = \frac{1}{x}\) |
| \(\tan \theta = \frac{y}{x}\) | \(\cot \theta = \frac{x}{y}\) |
Ahora usemos estas definiciones con los ángulos\(30^{\circ}\),\(150^{\circ}\),\(210^{\circ}\), y\(330^{\circ}\). Ya lo has hecho por\(30^{\circ}\). Aquí está ese dibujo:
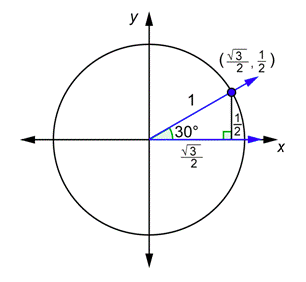
Los ángulos\(150^{\circ}\),\(210^{\circ}\), y\(330^{\circ}\) tienen algo en común. Cada uno de ellos tiene un ángulo de referencia de\(30^{\circ}\), como se puede ver en los dibujos a continuación. Debido a esto, es fácil encontrar las coordenadas de los puntos donde los lados terminales se cruzan con el círculo unitario usando el dibujo anterior.
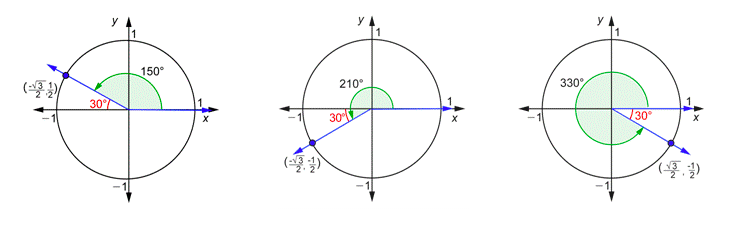
- Para el ángulo\(150^{\circ}\), este punto de intersección es la imagen especular de\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\) sobre el\(y\) eje, por lo que las coordenadas para\(150^{\circ}\) son\(\left(\frac{-\sqrt{3}}{2}, \frac{1}{2}\right)\).
- Para el ángulo\(210^{\circ}\), este punto es la imagen especular de\(\left(\frac{-\sqrt{3}}{2}, \frac{1}{2}\right)\) sobre el\(x\) eje, por lo que las coordenadas para\(210^{\circ}\) son\(\left(\frac{-\sqrt{3}}{2}, -\frac{1}{2}\right)\).
- Para el ángulo\(330^{\circ}\), este punto es la imagen especular de\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\) sobre el\(x\) eje, por lo que las coordenadas para\(330^{\circ}\) son\(\left(\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)\).
Ahora puede encontrar los valores de las seis funciones trigonométricas para\(150^{\circ}\),\(210^{\circ}\), y\(330^{\circ}\). Escojamos algunas funciones trigonométricas y evaluémoslas usando estos ángulos. Por ejemplo, usando el diagrama más a la izquierda anterior y la definición de coseno:
\ (\ begin {alineado}
\ cos\ theta &=x\\
\ cos 150^ {\ circ} &=\ frac {-\ sqrt {3}} {2}
\ end {alineado}\)
Usando el diagrama central y la definición de cotangente:
\ (\ begin {array} {c}
\ cuna\ theta=\ frac {x} {y}\
\ cuna 210^ {\ circ} =\ frac {\ frac {-\ sqrt {3}} {2}} {-\ frac {1} {2}} =\ frac {-\ sqrt {3}} {2}\ cdot\ frac {2}} {-1} =\ frac {-\ sqrt {3}} {-1} =\ sqrt {3}
\ end {array}\)
Usando el diagrama más a la derecha y la definición de cosecante:
\ (\ begin {array} {c}
\ csc\ theta=\ frac {1} {y}\
\ csc 330^ {\ circ} =\ frac {1} {-\ frac {1} {2}} =-2
\ end {array}\)
Si tomas el dibujo de arriba con el\(30^{\circ}\) ángulo en posición estándar, y giras el triángulo para que la pata más corta quede sobre el\(x\) eje, obtienes un dibujo de un\(60^{\circ}\) ángulo en posición estándar, como se ve a continuación.
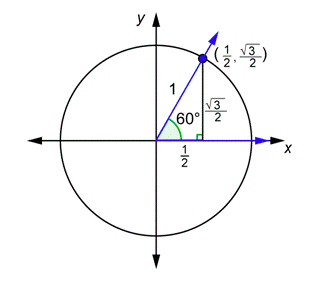
Puede utilizar la información de este diagrama para encontrar los valores de las seis funciones trigonométricas para cualquier ángulo que tenga un ángulo de referencia de\(60^{\circ}\).
Problema: Determinar\(\cos (300^{\circ})\) y\(\sec (300^{\circ})\).
Contestar
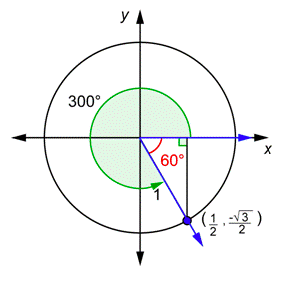
Dibuja\(300^{\circ}\) en posición estándar y encuentra el ángulo de referencia. Encuentra la\(x\) coordenada -del punto (\(x,y\)) donde el lado de la terminal intersecta el círculo unitario. Porque\(\cos 60^{\circ}=\frac{1}{2}\), ya sabemos\(x = \frac{1}{2}\).
Usa la definición de coseno. Sustituya el valor de la\(x\) coordenada -que encontraste arriba.
\ (\ begin {array} {c}
\ cos\ theta=x\
\ cos 300^ {\ circ} =\ frac {1} {2}
\ end {array}\)
Usa la definición de secante. Sustituya el valor de la\(x\) coordenada -que encontraste arriba. Tenga en cuenta que, al igual que con los ángulos agudos, la secante y el coseno son recíprocos.
\ (\ begin {array} {c}
\ seg\ theta=\ frac {1} {x}\\
\ seg 300^ {\ circ} =\ frac {1} {\ frac {1} {2}} =2
\ end {array}\)
\(\cos 300^{\circ}=\frac{1}{2}, \sec 300^{\circ}=2\)
El procedimiento es el mismo aunque el ángulo sea negativo. Recuerda que un ángulo negativo es simplemente aquel cuya dirección es en sentido horario.
Problema: Encontrar los valores de\(\sin (-120^{\circ})\) y\(\csc (-120^{\circ})\).
Contestar
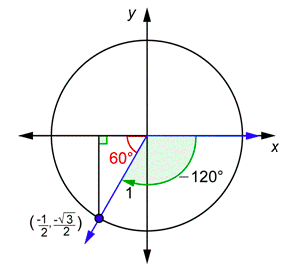
Dibuja\(-120^{\circ}\) en posición estándar y encuentra el ángulo de referencia. Encuentra la\(y\) coordenada -del punto (\(x,y\)) donde el lado de la terminal intersecta el círculo unitario.
Porque\(\sin 60^{\circ}=\frac{\sqrt{3}}{2}\) y estamos en el tercer cuadrante, lo sabemos\(y=-\frac{\sqrt{3}}{2}\).
Usa la definición de seno. Sustituya el valor de la\(y\) coordenada -que encontraste arriba.
\ (\ begin {array} {c}
\ sin\ theta=y\\
\ sin\ izquierda (-120^ {\ circ}\ derecha) =-\ frac {\ sqrt {3}} {2}
\ end {array}\)
Utilizar la definición de cosecante. Sustituya el valor de la\(y\) coordenada -que encontraste arriba. Racionalizar el denominador. Obsérvese que, al igual que con los ángulos agudos, el cosecante y el seno son recíprocos.
\ (\ begin {alineado}
\ csc\ theta &=\ frac {1} {y}\\ csc
\ izquierda (-120^ {\ circ}\ derecha) =\ frac {1} {\ frac {-\ sqrt {3}} {2}} &=-\ frac {2} {\ sqrt {3}}\ cdot\ frac {\ sqrt {3}}\ cdot\ frac {\ sqrt {\ sqrt {3} {3}} {\ sqrt {3}} =-\ frac {2\ sqrt {3}} {3}
\ final {alineado}\)
\(\sin \left(-120^{\circ}\right)=-\frac{\sqrt{3}}{2}, \csc \left(-120^{\circ}\right)=-\frac{2 \sqrt{3}}{3}\)
Observe los resultados de los dos últimos ejemplos y observe lo siguiente:
En cada caso, el valor de la función trigonométrica fue el mismo que el valor de esa función para el ángulo de referencia (\(60^{\circ}\)), o el negativo del valor de esa función para el ángulo de referencia. ¿Por qué sucedió esto? Los cálculos para\(60^{\circ}\) se realizaron usando el punto\(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\). Los cálculos para\(300^{\circ}\) y\(-120^{\circ}\) se realizaron usando los puntos\(\left(\frac{1}{2}, -\frac{\sqrt{3}}{2}\right)\) y\(\left(-\frac{1}{2}, -\frac{\sqrt{3}}{2}\right)\). Las\(x\) coordenadas -tienen el mismo valor absoluto. Las\(y\) coordenadas -también tienen el mismo valor absoluto. Cuando sustituyas en las expresiones\(x, \frac{1}{x}, y,\) y\(\frac{1}{y}\), el resultado será el mismo, o tendrá un signo negativo.
Obtendrás un resultado similar con otros ángulos. Por lo que el procedimiento para encontrar el valor de una función trigonométrica simplifica a lo siguiente:
- Determinar el ángulo de referencia.
- Calcular el valor de la función trigonométrica del ángulo de referencia.
- Determinar si el valor de la función es positivo o negativo.
Probemos este procedimiento en el siguiente ejemplo.
Problema:\(\tan (-45^{\circ})\) Cómputo y\(\cot (-45^{\circ})\).
Contestar
Dibuja el ángulo en posición estándar. El ángulo de referencia es\(45^{\circ}\).
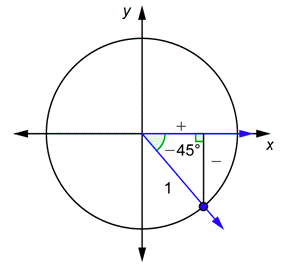
Usa el\(90^{\circ}\) triángulo\(45^{\circ}\)\(45^{\circ}\) - -. El valor de\(\tan 45^{\circ}\) es 1.
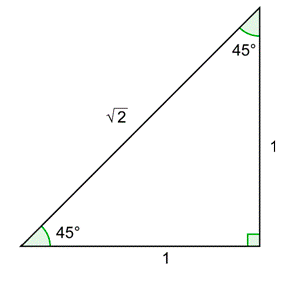
En el primer diagrama, ponemos un signo + para indicar que\(x\) es positivo, y un signo - para indicar que\(y\) es negativo. Use esto para determinar el signo de\(\tan (-45^{\circ})\).
\(\tan \left(-45^{\circ}\right)=\frac{y}{x}=\frac{(-)}{(+)}=(-)\)
Dado que el resultado fue negativo, el valor de\(\tan (-45^{\circ})\) es negativo.
\(\tan \left(-45^{\circ}\right)=-\tan 45^{\circ}=-1\)
Se puede pasar por un procedimiento similar con cotangente o utilizar el hecho de que es el recíproco de tangente.
\(\cot \left(-45^{\circ}\right)=\frac{1}{\tan \left(-45^{\circ}\right)}=\frac{1}{-1}=-1\)
\ (\ begin {array} {l}
\ tan\ left (-45^ {\ circ}\ derecha) =-1\\
\ cot\ izquierda (-45^ {\ circ}\ derecha) =-1
\ end {array}\)
Los ángulos cuyas medidas son múltiples\(90^{\circ}\) tienen lados terminales en los ejes. Esto puede resultar confuso, porque el lado terminal no está en un cuadrante, sino más bien en una frontera entre cuadrantes. Entonces veamos estos ángulos por separado. El siguiente dibujo muestra los puntos de intersección de los lados terminales de\(0^{\circ}\),\(90^{\circ}\),\(180^{\circ}\), y\(270^{\circ}\) con el círculo unitario.
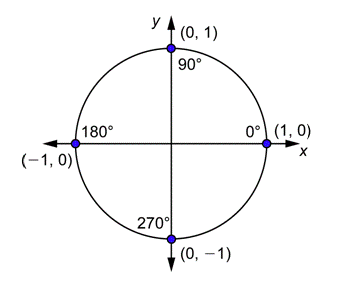
Puede utilizar este dibujo y las definiciones para encontrar las funciones trigonométricas para (0^ {\ circ}\),\(90^{\circ}\),\(180^{\circ}\), y\(270^{\circ}\). Por ejemplo:
\ (\ begin {array} {c}
\ sin\ theta=y\\
\ sin 0^ {\ circ} =0\\
\ sin 90^ {\ circ} =1\\
\ sin 180^ {\ circ} =0\\
\ sin 270^ {\ circ} =-1
\ end {array}\)
Para las seis funciones, se sustituyen los valores de\(x\) y\(y\) como lo hizo antes. No obstante, ¿qué pasa si intentas calcular\(\tan 90^{\circ}\) usando la definición\(\tan \theta=\frac{y}{x}\)?
\ (\ begin {array} {c}
\ tan\ theta=\ frac {y} {x}\\
\ tan 90^ {\ circ} =? \ frac {1} {0}
\ end {array}\)
No se puede dividir por 0, entonces\(\tan 90^{\circ}\) es simplemente indefinido. De igual manera,\(\csc 180^{\circ}\) es indefinido, porque si intentas aplicar la definición, terminarás dividiendo por 0. Lo mismo ocurre cada vez que una de las definiciones lleva a la división por 0: la función trigonométrica no está definida para ese ángulo.
¿Cuáles son los valores de\(\cos 90^{\circ}\) y\(\cot 180^{\circ}\)?
- \(\cos 90^{\circ}=0 \text { and } \cot 180^{\circ}=0\)
- \(\cos 90^{\circ}=0 \text { and } \cot 180^{\circ}=\text { undefined }\)
- \(\cos 90^{\circ}=1 \text { and } \cot 180^{\circ}=0\)
- \(\cos 90^{\circ}=1 \text { and } \cot 180^{\circ}=\text { undefined }\)
- Contestar
-
- \(\cos 90^{\circ}=0 \text { and } \cot 180^{\circ}=0\). Incorrecto. El valor para coseno es correcto. Sin embargo, al evaluar la cotangente, es posible que haya cambiado las\(y\) coordenadas\(x\) - y -. La respuesta correcta es B.
- \(\cos 90^{\circ}=0 \text { and } \cot 180^{\circ}=\text { undefined }\). Correcto. Desde\(\cos \theta = x\) y\(90^{\circ}\) corresponde al punto (0,1),\(\cos 90 = 0\). Ahora\(\cot \theta=\frac{x}{y}\) y\(180^{\circ}\) corresponde al punto (-1,0). Si intentaras aplicar la definición estarías dividiendo por 0, porque\(y = 0\). Esto quiere decir que no\(\cot 180^{\circ}\) está definido.
- \(\cos 90^{\circ}=1 \text { and } \cot 180^{\circ}=0\). Incorrecto. Al evaluar ambas funciones, es posible que haya cambiado las\(y\) coordenadas\(x\) - y -. La respuesta correcta es B.
- \(\cos 90^{\circ}=1 \text { and } \cot 180^{\circ}=\text { undefined }\). Incorrecto. El valor de cotangente es correcto. Sin embargo, al evaluar el coseno, es posible que haya cambiado las\(y\) coordenadas\(x\) - y -. La respuesta correcta es B.
Puede utilizar los siguientes gráficos para ayudarle a recordar los valores de las funciones trigonométricas para los ángulos de referencia\(0^{\circ}\)\(30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\), y\(90^{\circ}\) para seno y coseno. Una vez que se tienen estos, se puede obtener el valor de tangente de la identidad\(\tan \theta=\frac{\sin \theta}{\cos \theta}\), y los valores de las otras tres funciones trigonométricas utilizando reciprocales.
Haz una tabla de la siguiente manera:
| \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | |
| seno | |||||
| coseno |
Como paso inicial, ponga los números 0, 1, 2, 3 y 4 en la fila “seno” y 4, 3, 2, 1 y 0 en la fila “coseno”. Haz esto a lápiz. ¡Vas a reemplazar estos números!
| \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | |
| seno | 0 | 1 | 2 | 3 | 4 |
| coseno | 4 | 3 | 2 | 1 | 0 |
Ahora reemplace los números del 0 al 4 tomando sus raíces cuadradas y dividiendo por 2. Las filas ahora contienen los valores correctos, pero no simplificados, para seno y coseno.
| \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | |
| seno | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) |
| coseno | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) |
Se puede simplificar\(\sqrt{0}\) a 0,\(\sqrt{1}\) a 1 y\(\sqrt{4}\) a 2, y luego dividir por 2. Esto te dará la tabla final con los valores correctos de seno y coseno en estos ángulos.
| \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | |
| seno | 0 | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | 1 |
| coseno | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | 0 |
Determinación del Signo de las Funciones Trigonométricas
Primero aprendiste las definiciones de las funciones trigonométricas de un ángulo agudo. Después aprendiste las definiciones generales de estas funciones, que pueden ser utilizadas para cualquier ángulo, y el método para aplicarlas. Finalmente, aprendiste un procedimiento más sencillo para encontrar los valores de las funciones trigonométricas:
- Determinar el ángulo de referencia.
- Calcular el valor de la función trigonométrica del ángulo de referencia.
- Determinar si el valor de la función es positivo o negativo.
Ahora aprenderás una manera fácil de recordar dónde son positivas las funciones trigonométricas y dónde son negativas.
La función sinusoidal: ya que\(\sin \theta = y\), seno es positivo cuando\(y > 0\). Esto ocurre en los Cuadrantes I y II.
La función coseno: ya que\(\cos \theta = x\), coseno es positivo cuando\(x > 0\). Esto ocurre en los Cuadrantes I y IV.
La función tangente: ya que\(\tan \theta=\frac{y}{x}\), tangente es positiva cuando\(x\) y ambas\(y\) son positivas o ambas negativas. Esto ocurre en los Cuadrantes I y III.
Podemos resumir esta información por cuadrante:
Cuadrante I: seno, coseno y tangente son positivos.
Cuadrante II: el seno es positivo (coseno y tangente son negativos).
Cuadrante III: la tangente es positiva (seno y coseno son negativos).
Cuadrante IV: el coseno es positivo (el seno y la tangente son negativos).
Deje que A represente todos (tres funciones, seno, coseno y tangente), S significa seno, T significa tangente y C significa coseno. Ahora puedes usar estas letras simples para recordar en qué cuadrante seno, coseno y tangente son positivos. El paso final es reemplazar cada letra por una palabra para darte una frase que sea fácil de recordar: “A ll S tudents T ake C alculus”. Yendo en sentido antihorario, coloca estas palabras en los cuatro cuadrantes.
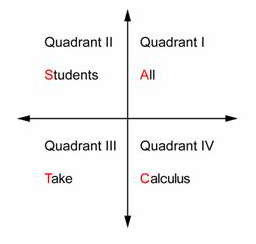
Ahora si miras en el Cuadrante II, por ejemplo, ves la palabra S tudentes. La S te dice que el s ine es positivo (mientras que el coseno y la tangente son negativos).
Problema: ¿Qué señales son\(\tan 200^{\circ}\) y\(\cos 200^{\circ}\)?
Contestar
Ya que\(200^{\circ} = 180^{\circ} + 20^{\circ}\), está en el Cuadrante III.
La palabra “Tomar” representa el hecho de que la tangente es positiva, así\(\tan 200^{\circ}\) es positiva.
El seno y el coseno son negativos en el Cuadrante III, por lo que\(\cos 200^{\circ}\) es negativo.
\ (\ begin {array} {l}
\ tan 200^ {\ circ}\ text {es positivo y}\\
\ cos 200^ {\ circ}\ text {es negativo.}
\ end {array}\)
Problema: ¿En qué cuadrante debe estar un ángulo si su seno es positivo y su tangente es negativa?
Contestar
Las palabras “Todos” y “Estudiantes” nos dicen que el seno es positivo en los Cuadrantes I y II.
La tangente es positiva en el Cuadrante I, pero negativa en el Cuadrante II.
Cuadrante II
Este dispositivo se aplica a las funciones seno, coseno y tangente. Las otras tres funciones trigonométricas son recíprocas de estas tres. Recordemos el hecho básico de que el recíproco de un número positivo es positivo, y el recíproco de un número negativo es negativo. Esto implica que seno y cosecante tienen el mismo signo, coseno y secante tienen el mismo signo, y tangente y cotangente tienen el mismo signo. Entonces, si quieres conocer el signo de cosecante, secante o cotangente, encuentra el signo de seno, coseno, o tangente, respectivamente.
¿Qué señales son\(\cos (-25^{\circ})\) y\(\sec (-25^{\circ})\)?
- Ambos son positivos.
- Ambos son negativos.
- \(\cos (-25^{\circ})\)> 0 y\(\sec (-25^{\circ})\) < 0
- \(\cos (-25^{\circ})\)< 0 y\(\sec (-25^{\circ})\) > 0
- Contestar
-
- Ambos son positivos. Correcto. \(-25^{\circ}\)El ángulo está en el Cuadrante IV. La palabra “Cálculo” te dice que el coseno es positivo. Dado que la secante es el recíproco del coseno, también es positiva.
- Ambos son negativos. Incorrecto. Quizás pensaste que debido a que el ángulo es negativo, los valores de estas funciones serían negativos. Los valores dependen del cuadrante en el que se encuentra el ángulo. Ángulo\(-25^{\circ}\) se encuentra en el Cuadrante IV. La respuesta correcta es A.
- \(\cos (-25^{\circ})\)> 0 y\(\sec (-25^{\circ})\) < 0. Incorrecto. El signo del coseno es correcto. Quizás pensaste que cuando tomas un recíproco, el signo cambia, pero el signo no cambia. Por lo tanto, secante y coseno tienen el mismo signo. La respuesta correcta es A.
- \(\cos (-25^{\circ})\)< 0 y\(\sec (-25^{\circ})\) > 0. Incorrecto. El signo de secante es correcto. Quizás pensaste que debido a que el ángulo es negativo, el valor del coseno sería negativo. Los valores dependen del cuadrante en el que se encuentra el ángulo. Ángulo\(-25^{\circ}\) se encuentra en el Cuadrante IV. La respuesta correcta es A.
Resumen
Las funciones trigonométricas se definieron originalmente para ángulos agudos. Existen definiciones generales de estas funciones, las cuales se aplican a ángulos de cualquier tamaño, incluidos los ángulos negativos. Los valores de las funciones trigonométricas se calculan encontrando el ángulo de referencia, determinando el valor de la función trigonométrica del ángulo de referencia, y luego determinando si el valor de la función es positivo o negativo. Una manera útil de recordar este último paso es “A ll S tudents T ake C alculus”.