19.2.1: Medida de Grado y Radianes
- Page ID
- 111220
- Entender la medida de radián.
- Convertir de grado a medida de radianes.
- Convertir de radián a medida de grado.
Introducción
Sabes que puede haber diferentes unidades de medida para medir lo mismo. Por ejemplo, la longitud se puede medir en pies y metros y la temperatura se puede medir en grados Celsius y grados Fahrenheit. A menudo utilizamos fórmulas para convertir entre diferentes unidades de medida.
También hay dos formas de medir ángulos. Ya sabes medirlos en grados. Ahora aprenderás a medirlos en radianes y a convertir entre estas dos mediciones. Si bien la medida de grado se usa en actividades cotidianas como la construcción de edificios y la topografía de terrenos, la medida de radianes se usa para muchos cálculos, como la velocidad y la distancia recorrida por los satélites sobre la superficie de la Tierra, ¡incluida la Estación Espacial Internacional! Es importante poder medir ángulos tanto en radianes como en grados y poder convertir entre los dos sistemas.
Medida de radián
Para que podamos definir radianes, es necesario introducir el concepto de ángulo central. Un ángulo central es un ángulo cuyo vértice está en el centro de un círculo. En el círculo de abajo, el centro es punto\(O\), la longitud del radio es\(r\), y\(\angle AOB\) es un ángulo central.
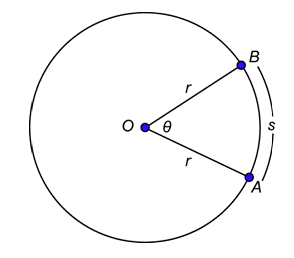
Observe que\(\angle AOB\) corta o determina un arco\(\stackrel{\large \frown}{AB}\) que tiene longitud\(s\). La medida radianes de un ángulo central, a menudo denotada por la letra griega theta (\(\theta\)), se define como la relación entre la longitud del arco y la longitud del radio. Entonces la medida radianes de\(\angle AOB\) viene dada por:
\(\theta=\frac{\text { arc length }}{\text { radius length }}=\frac{s}{r}\)
La longitud del arco\(s\), y el radio\(r\),, deben estar en las mismas unidades.
Problema: ¿Cuál es la medida radianes del ángulo central\(AOB\)?
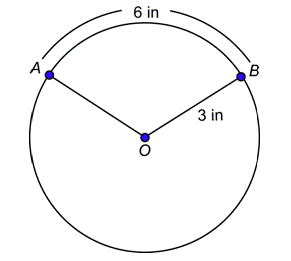
Contestar
En este círculo,\(r = 3\) pulgadas. El arco determinado por\(\angle AOB\) tiene\(s = 6\) pulgadas de longitud. Sustitúyalos en la fórmula.
\(\theta=\frac{s}{r}=\frac{6 \text { inches }}{3 \text { inches }}=2\)
La medida del ángulo central\(AOB\) es de 2 radianes.
Problema: Encuentra la medida del ángulo central\(AOB\) en radianes.
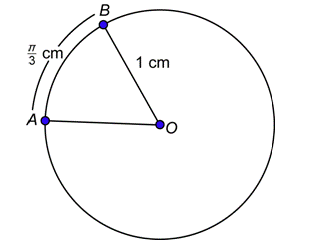
Contestar
En este círculo,\(r = 1\) cm. El arco determinado por\(\angle AOB\) tiene longitud\(s = \frac{\pi}{3}\) cm. Sustitúyalos en la fórmula.
\(\theta=\frac{s}{r}=\frac{\frac{\pi}{3} \mathrm{~cm}}{1 \mathrm{~cm}}=\frac{\pi}{3}\)
La medida del ángulo central\(AOB\) es\(\frac{\pi}{3}\) radianes.
¿Cuál es la conexión entre grados y radianes? Veamos qué pasa cuando el arco es todo el círculo:
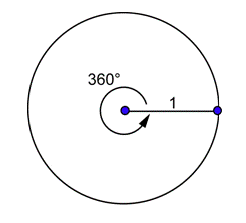
La circunferencia de este círculo viene dada por\(C=2 \pi r=2 \pi \cdot 1=2 \pi\). Esta es la longitud del arco de todo el círculo, o la longitud del arco correspondiente a un ángulo central de\(360^{\circ}\). ¿Cuál es la medida radianes de este ángulo?
\(\theta=\frac{\text { arc length }}{\text { radius length }}=\frac{2 \pi}{1}=2 \pi\)
Un ángulo central de\(360^{\circ}\) tiene una medida radianes de\(2\pi\). Es decir:
\(360^{\circ}=2 \pi \text { radians }\)
Si divide ambos lados por 2, obtendrá:
\(180^{\circ}=\pi \text { radians }\)
Usaremos esto para convertir de grados a radianes y viceversa.
Mientras que los grados siempre se escriben con un símbolo de grado (°), los radianes generalmente se escriben sin ningún símbolo o unidad adjunta. Entonces, por ejemplo,\(\tan 3^{\circ}\) significa la tangente de un ángulo que mide\(3^{\circ}\), mientras que\(\tan 3\) significa la tangente de un ángulo que mide 3 radianes.
Asegúrese de usar las mismas unidades de longitud para la longitud del radio\(r\) y la longitud del arco\(s\). En el primer ejemplo, ambos estaban en pulgadas; en el segundo ejemplo, ambos estaban en centímetros. Cuando divides, esas unidades se cancelan y te quedan con un número sin unidades.
Problema: Encuentra la medida del ángulo central\(AOB\) en radianes.
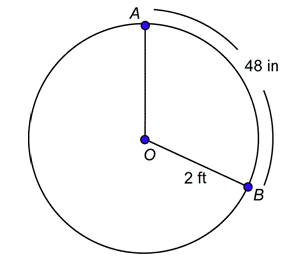
Contestar
Quieres que la longitud del arco y el radio tengan las mismas unidades, pero se te dan en pulgadas y pies. Podrías convertir cualquiera de los dos. El arco determinado por\(\angle AOB\) tiene\(s = 48\) pulgadas de longitud.
\ (\ begin {array} {l}
s =48\ texto {pulgadas}\
\,\,\, =48\ texto {pulgadas}\ cdot\ frac {1\ texto {pie}} {12\ texto {pulgadas}}\\
\,\,\, =4\ texto {pies}
\ end {array}\)
En este círculo,\(r = 2\) pies. Sustituya este y el valor anterior por\(s\) en la fórmula.
\(\theta=\frac{s}{t}=\frac{4 \text { feet }}{2 \text { feet }}=2\)
La medida del ángulo central\(AOB\) es de 2 radianes.
Si toma la definición de medida de radianes\(\theta = \frac{s}{r}\), y multiplica ambos lados por r, obtiene la fórmula para la longitud del arco:
\(s=r \theta\)
Problema: El ángulo central mostrado tiene una medida de\(\frac{1}{2}\) radián. ¿Cuál es la longitud de\(\stackrel {\large \frown}{CD}\)?
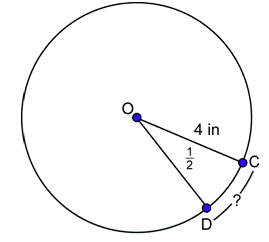
Contestar
En este círculo,\(r = 4\) pulgadas. Eso ya lo sabes\(\theta = \frac{1}{2}\). Sustituya estos números en la fórmula de longitud de arco.
\(s=r \theta=(4 \text { inches }) \cdot \frac{1}{2}=2 \text { inches }\)
La longitud de\(\stackrel {\large \frown}{CD}\) es de 2 pulgadas.
Hemos utilizado\(\theta = \frac{s}{t}\) y\(s = r \theta\) para encontrar la medida radianes del ángulo central así como la longitud del arco. Pero también puedes usar la fórmula de longitud de arco para encontrar la longitud del radio, como se ve en el siguiente ejemplo.
Problema: Si la longitud de\(\stackrel {\large \frown}{EF}\) es de 42 milímetros, y la medida de\(\angle EOF\) es de 3 radianes, ¿cuál es la longitud del radio del círculo?
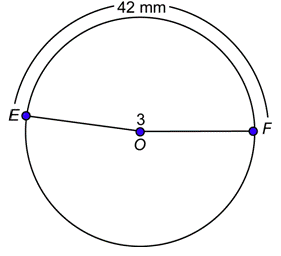
Contestar
Se le da ese\(s = 42\) mm, y\(\theta = 3\). Sustituya estos valores en la fórmula de longitud de arco.
\ (\ begin {array} {c}
s=r\ theta\\
42\ mathrm {~mm} =r\ cdot 3
\ end {array}\)
Resuelve la ecuación para\(r\).
\(\frac{42 \mathrm{~mm}}{3}=r\)
Reescribir como un número mixto.
\(r=14 \mathrm{~mm}\)
El radio del círculo es de 14 milímetros.
Un círculo tiene un radio de 8 pulgadas y el ángulo central\(AOB\) hace un arco\(AB\) de 2 pies de longitud.
¿Cuál es la medida radianes del ángulo\(AOB\)?
- \(\frac{1}{4}\)
- \(\frac{1}{3}\)
- 3
- 4
- Contestar
-
- \(\frac{1}{4}\). Incorrecto. Probablemente dividiste 2 por 8. Necesitas convertir los pies a pulgadas para que tengas las mismas unidades. La respuesta correcta es 3.
- \(\frac{1}{3}\). Incorrecto. Probablemente convertiste correctamente ambas medidas a pulgadas, pero luego dividiste el radio por la longitud del arco. Es necesario dividir la longitud del arco por el radio. La respuesta correcta es 3.
- 3. Correcto. La longitud del arco es de 2 pies o 24 pulgadas. Divide esto por el radio, 8 pulgadas, para obtener 3.
- 4. Incorrecto. Probablemente dividiste 8 por 2. Necesitas convertir los pies a pulgadas para que tengas las mismas unidades. También es necesario dividir la longitud del arco por el radio. La respuesta correcta es 3.
Conversión de Grados a Radianes
Antes vimos eso\(180^{\circ}\) =\(\pi\) radianes. Divide ambos lados de esta ecuación por 180. Obtienes:
\(1^{\circ}=\frac{\pi}{180} \text { radians }\)
Puedes usar esto para convertir la medida de un ángulo de grados a radianes. Por ejemplo, si quisieras convertir\(30^{\circ}\) a radianes, podrías multiplicar ambos lados por 30:
\(30^{\circ}=30 \cdot \frac{\pi}{180} \text { radians }=\frac{30 \pi}{180} \text { radians }=\frac{\pi}{6} \text { radians }\)
Para decirlo de otra manera, se multiplica\(30^{\circ}\) por\(\frac{\pi}{180^{\circ}}\) para obtener\(\frac{\pi}{6}\) radianes.
Para convertir\(60^{\circ}\) a radianes, se multiplica\(60^{\circ}\) por\(\frac{\pi}{180^{\circ}}\) para obtener\(\frac{\pi}{3}\) radianes.
De manera similar, multiplique cualquier medida de grado por\(\frac{\pi}{180^{\circ}}\) para convertirla en radianes.
Problema: Convertir\(0^{\circ}\),\(45^{\circ}\),\(90^{\circ}\) a radianes.
Contestar
En cada caso, simplemente multiplique por\(\frac{\pi}{180^{\circ}}\) y simplifique.
\(0^{\circ}=0^{\circ} \cdot \frac{\pi}{180^{\circ}} \text { radians }=0 \text { radians }\)
\ (\ begin {alineado}
45^ {\ circ} &=45^ {\ circ}\ cdot\ frac {\ pi} {180^ {\ circ}}\ text {radianes}\\
&=\ frac {45\ pi} {180}\ text {radianes}\\
&=\ frac {\ pi} {4}\ texto {radianes}
\ end {alineado}\)
\ (\ begin {alineado}
90^ {\ circ} &=90^ {\ circ}\ cdot\ frac {\ pi} {180^ {\ circ}}\ text {radianes}\\
&=\ frac {90\ pi} {180}\ text {radianes}\\
&=\ frac {\ pi} {2}\ texto {radianes}
\ end {alineado}\)
\(0^{\circ}=0 \text { radians, } 45^{\circ}=\frac{\pi}{4} \text { radians, } 90^{\circ}=\frac{\pi}{2} \text { radians }\)
Aquí hay un gráfico con los ángulos que hemos convertido hasta ahora.
| Medida de Grado | Medida de radianes |
| \(0^{\circ}\) | 0 |
| \(30^{\circ}\) | \(\frac{\pi}{6}\) |
| \(45^{\circ}\) | \(\frac{\pi}{4}\) |
| \(60^{\circ}\) | \(\frac{\pi}{3}\) |
| \(90^{\circ}\) | \(\frac{\pi}{2}\) |
| \(180^{\circ}\) | \(\pi\) |
| \(360^{\circ}\) | \(2 \pi\) |
Aquí está la misma información, con algunos ángulos adicionales, en formato de imagen:
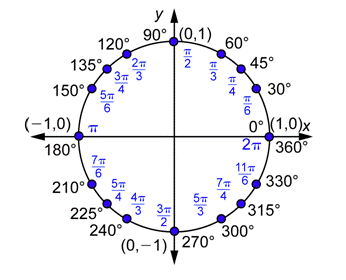
El mismo procedimiento funciona igual de bien para ángulos negativos. Recuerde que un ángulo negativo es solo un ángulo que se orienta en sentido horario cuando se dibuja en posición estándar. Un número negativo de grados se convierte en un número negativo de radianes.
¿En cuántos radianes hay\(-120^{\circ}\)?
- \(\frac{\pi}{60}\)
- \(-\frac{2}{3}\)
- \(-\frac{3 \pi}{2}\)
- \(-\frac{2 \pi}{3}\)
- Contestar
-
- \(\frac{\pi}{60}\). Incorrecto. Es posible que hayas encontrado correctamente\(-\frac{120 \pi}{180}\), pero luego reducido incorrectamente. La respuesta correcta es D.
- \(-\frac{2}{3}\). Incorrecto. Parece que te dividiste por 180. Necesitas multiplicar por\(\frac{\pi}{180^{\circ}}\). La respuesta correcta es D.
- \(-\frac{3 \pi}{2}\). Incorrecto. Es posible que hayas encontrado correctamente\(-\frac{120 \pi}{180}\), pero cometiste un error al reducir. La respuesta correcta es D.
- \(-\frac{2 \pi}{3}\). Correcto. Multiplicar por\(\frac{\pi}{180^{\circ}}\) para obtener\(-\frac{120 \pi}{180}=-\frac{2 \pi}{3}\).
Conversión de Radianes a Grados
Supongamos que tenías ángulos medidos en radianes y querías saber su medida de grado. El procedimiento es similar al que va de grados a radianes.
Otra vez, ya sabes que\(\pi\) radianes\(= 180^{\circ}\). Dividir ambos lados de esta ecuación por\(\pi\). Obtienes:
\(\text { radian }=\frac{180^{\circ}}{\pi}\)
Si quisieras convertir\(\frac{\pi}{6}\) radianes a grados, podrías multiplicar ambos lados de la ecuación anterior por\(\frac{\pi}{6}\):
\(\frac{\pi}{6} \cdot 1 \text { radian }=\frac{\pi}{6} \cdot \frac{180^{\circ}}{\pi}=\frac{180^{\circ}}{6}=30^{\circ}\)
Para afirmar esto de otra manera, nos multiplicamos\(\frac{\pi}{6}\) por\(\frac{180^{\circ}}{\pi}\) para conseguir\(30^{\circ}\). De manera similar, multiplique cualquier medida de radianes por\(\frac{180^{\circ}}{\pi}\) para convertirla a grados.
Problema: Convertir\(\frac{2 \pi}{3}\) y\(\frac{3 \pi}{4}\) a grados.
Contestar
En cada caso, simplemente multiplique por\(\frac{180^{\circ}}{\pi}\) y simplifique.
\ (\ begin {alineado}
\ frac {2\ pi} {3} &=\ frac {2\ pi} {3}\ cdot\ frac {180^ {\ circ}} {\ pi}\\
&=\ frac {360^ {\ circ}} {3}\\
&=120^ {\ circ}
\ end {alineado}\)
\ (\ begin {alineado}
\ frac {3\ pi} {4} &=\ frac {3\ pi} {4}\ cdot\ frac {180^ {\ circ}} {\ pi}\\
&=\ frac {540^ {\ circ}} {4}\\
&=135^ {\ circ}
\ end {alineado}\)
\(\frac{2 \pi}{3}=120^{\circ}, \frac{3 \pi}{4}=135^{\circ}\)
Asegúrate de que tu respuesta tenga un símbolo de grado. Siempre se supone que una medida de ángulo escrita sin un símbolo de grado está en radianes.
Aquí hay un gráfico que muestra medidas equivalentes de radianes y grados para algunos ángulos comunes.
| Medida de radianes | Medida de Grado |
| 0 | \(0^{\circ}\) |
| \ frac {\ pi} {6} | \(30^{\circ}\) |
| \ frac {\ pi} {4} | \(45^{\circ}\) |
| \ frac {\ pi} {3} | \(60^{\circ}\) |
| \ frac {\ pi} {2} | \(90^{\circ}\) |
| \(\pi\) | \(180^{\circ}\) |
| \(2 \pi\) | \(360^{\circ}\) |
Problema: Convierte 1 radián a grados y da tu respuesta al décimo de grado más cercano.
Contestar
En realidad, ya se conoce el valor de 1 radián en grados. No obstante, es necesario utilizar una calculadora para hacer la división y obtener un decimal.
\ (\ begin {alineado}
1\ text {radián} &=\ frac {180^ {\ circ}} {\ pi}\\
&=57.29577951^ {\ circ}\ ldots\\
&= aproximadamente 57.3^ {\ circ}
\ end {alineado}\)
\(1 \text { radian } \approx 57.3^{\circ}\)
Entonces 1 radián es un poco menos de\(60^{\circ}\), o un poco menos de una sexta parte de un círculo.
Se puede utilizar el mismo procedimiento para ángulos negativos.
¿Cuál es la medida de grado equivalente de\(-\frac{5 \pi}{6}\) radianes escrita en términos más simples?
- \(150^{\circ}\)
- \(-150^{\circ}\)
- \(\frac{-900^{\circ}}{6}\)
- \(\frac{-\pi^{2}}{216}\)
- Contestar
-
- \(150^{\circ}\). Incorrecto. Probablemente multiplicaste correctamente por\(\frac{180^{\circ}}{\pi}\), pero dejaste fuera el signo negativo. La respuesta correcta es\(-150^{\circ}\).
- \(-150^{\circ}\). Correcto. \(\frac{180^{\circ}}{\pi}\)Multiplicar por para obtener\(\frac{-900 \pi^{\circ}}{6 \pi}\), y luego simplificar la fracción.
- \(\frac{-900^{\circ}}{6}\). Incorrecto. Probablemente multiplicaste correctamente por\(\frac{180^{\circ}}{\pi}\), pero olvidaste simplificar. La respuesta correcta es\(-150^{\circ}\).
- \(\frac{-\pi^{2}}{216}\). Incorrecto. Te multiplicaste por\(\frac{\pi}{180^{\circ}}\) en lugar de\(\frac{180^{\circ}}{\pi}\). Además, cuando escribes un ángulo en grados, debes usar un símbolo de grado, y esta opción de respuesta no tiene uno. La respuesta correcta es\(-150^{\circ}\).
Resumen
Los ángulos se pueden medir de dos maneras: con grados y radianes. La medida de radianes de un ángulo central se define como la relación entre la longitud del arco y la longitud del radio. Esta definición conduce a la fórmula de longitud del arco:\(s=r \theta\).
Radianes y grados están conectados por la relación\(360^{\circ}=2 \pi \text { radians }\). Si desea convertir de grados a radianes, multiplique la medida de grado por\(\frac{\pi}{180^{\circ}}\). Si desea convertir de radianes a grados, multiplique la medida de radianes por\(\frac{180^{\circ}}{\pi}\).