9.1: Presentación gráfica de datos categóricos
- Page ID
- 112898
Los datos categóricos o cualitativos son piezas de información que nos permiten clasificar los objetos investigados en diversas categorías. Por lo general, comenzamos a trabajar con datos categóricos resumiendo los datos en una tabla de frecuencias.
Una tabla de frecuencias es una tabla con dos columnas. Una columna enumera las categorías, y otra para las frecuencias con las que ocurren los ítems en las categorías (cuántos elementos encajan en cada categoría).
Una compañía de seguros determina las primas de seguro de vehículos en función de factores de riesgo conocidos. Si a una persona se le considera un riesgo mayor, sus primas serán mayores. Un factor potencial es el color de tu auto. La compañía de seguros cree que las personas con algunos autos de color tienen más probabilidades de meterse en accidentes. Para investigar esto, examinan informes policiales para detectar colisiones recientes de pérdida total. Los datos se resumen en la tabla de frecuencias a continuación.
| Color | Frecuencia |
| Azul | 25 |
| Verde | 52 |
| Rojo | 41 |
| Blanco | 36 |
| Negro | 39 |
| Gris | 23 |
A veces necesitamos una forma aún más intuitiva de mostrar datos. Aquí es donde entran los cuadros y gráficos. Hay muchas, muchas formas de mostrar los datos gráficamente, pero nos concentraremos en un tipo de gráfico muy útil llamado gráfico de barras. En esta sección, trabajaremos con gráficos de barras que muestren datos categóricos; la siguiente sección estará dedicada a gráficas que muestren datos cuantitativos.
Un gráfico de barras es un gráfico que muestra una barra para cada categoría con la longitud de cada barra indicando la frecuencia de esa categoría.
Tenga en cuenta que un gráfico de barras solo se usa para mostrar datos categóricos.
Para construir un gráfico de barras, necesitamos dibujar un eje vertical y un eje horizontal. La dirección vertical tendrá una escala y medirá la frecuencia de cada categoría; el eje horizontal no tiene escala en esta instancia, sino sólo los nombres de cada categoría. La construcción de un gráfico de barras se describe más fácilmente mediante el uso de un ejemplo.
Usando los datos de nuestro automóvil desde arriba, tenga en cuenta que la frecuencia más alta es 52, por lo que nuestro eje vertical necesita ir de 0 a 52, pero bien podríamos usar 0 a 55, para que podamos poner una marca hash cada 5 unidades:
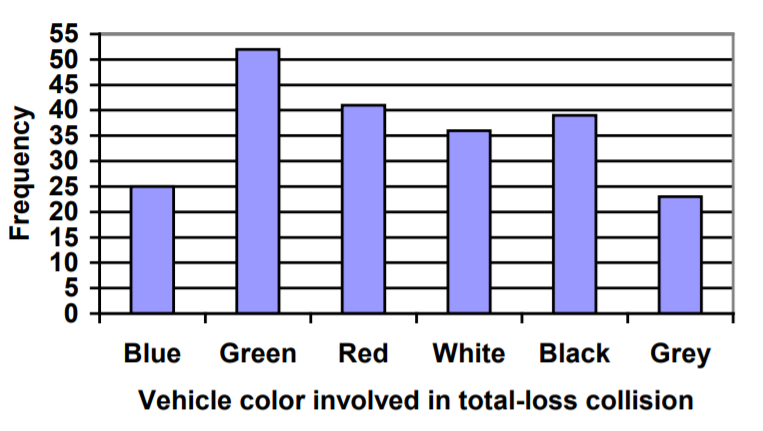
Observe que la altura de cada barra está determinada por la frecuencia del color correspondiente. Las cuadrículas horizontales son un toque agradable, pero no necesario. En la práctica, te resultará útil dibujar gráficos de barras usando papel cuadrilátero, por lo que las líneas de cuadrícula ya estarán en su lugar, o usando tecnología. En lugar de líneas de cuadrícula, también podríamos enumerar las frecuencias en la parte superior de cada barra, así:
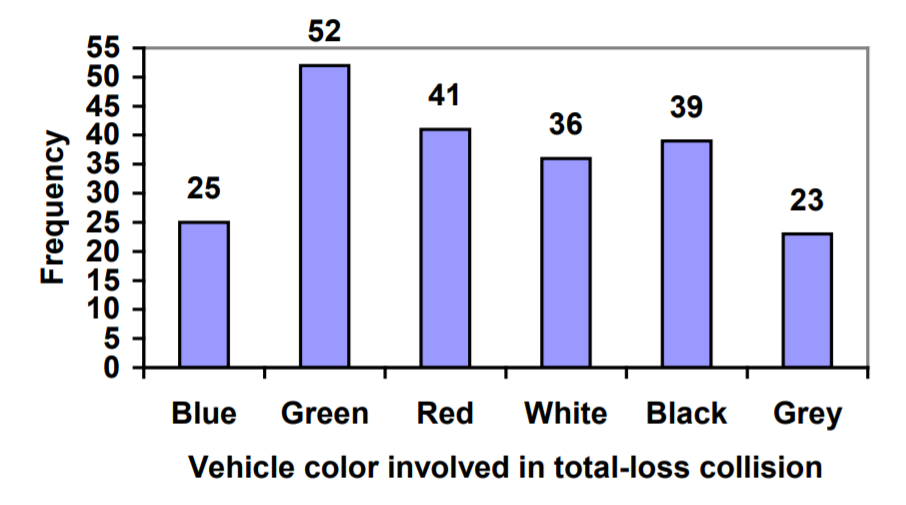
En este caso, nuestro gráfico podría beneficiarse de ser reordenado de los valores de frecuencia más grandes a los más pequeños. Esta disposición puede facilitar la comparación de valores similares en el gráfico, incluso sin líneas de cuadrícula. Cuando organizamos las categorías en orden decreciente de frecuencia así, se llama gráfico de Pareto.
Un gráfico de Pareto es un gráfico de barras ordenado de mayor a menor frecuencia.
Transformando nuestro gráfico de barras de antes en un gráfico de Pareto, obtenemos:
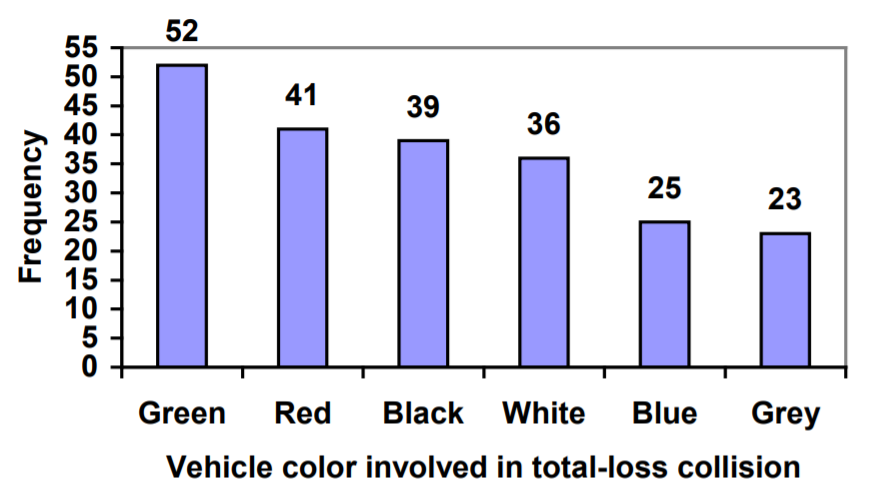
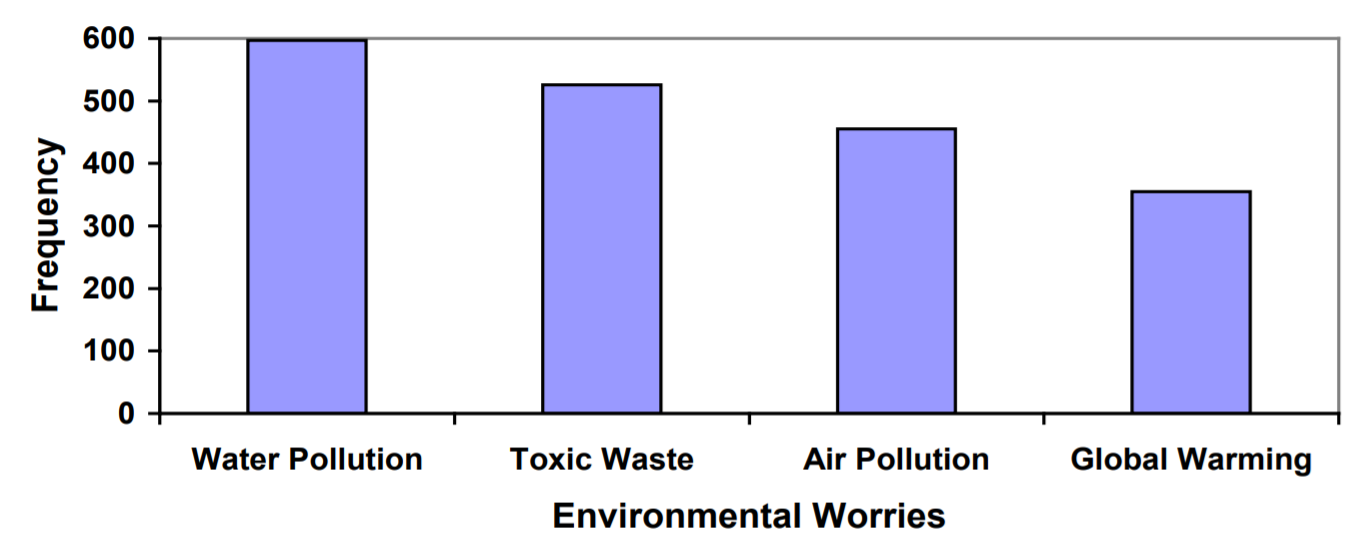
En una encuesta [1], se les preguntó a los adultos si personalmente les preocupaba una variedad de preocupaciones ambientales. A continuación se resumen los números (de 1012 encuestados) que indicaron que les preocupaban “mucho” por algunas inquietudes seleccionadas.
| Emisión Ambiental | Frecuencia |
| Contaminación del agua potable | 597 |
| Contaminación del suelo y del agua por residuos tóxicos | 526 |
| Contaminación del aire | 455 |
| Calentamiento global | 354 |
Estos datos podrían mostrarse gráficamente en un gráfico de barras:
Para mostrar tamaños relativos, es común usar un gráfico circular.
Un gráfico circular es un círculo con cuñas cortadas de diferentes tamaños marcadas como rebanadas de pastel o pizza. Los tamaños relativos de las cuñas corresponden a las frecuencias relativas de las categorías.
Para nuestros datos de color de vehículos, un gráfico circular podría verse así:
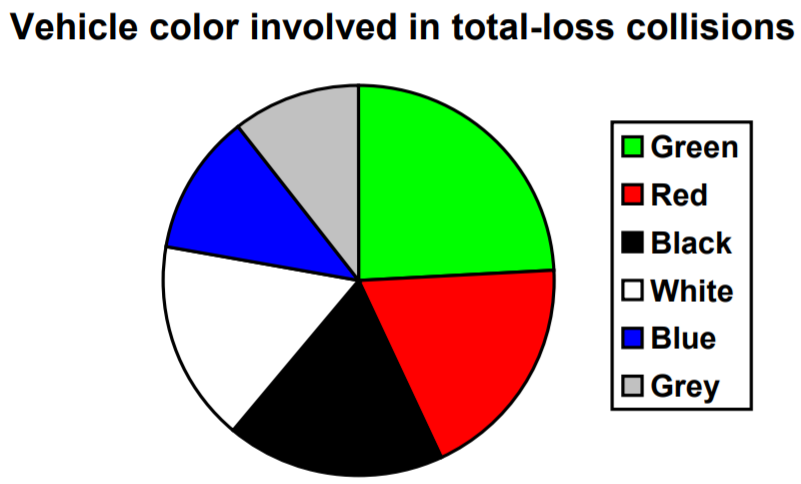
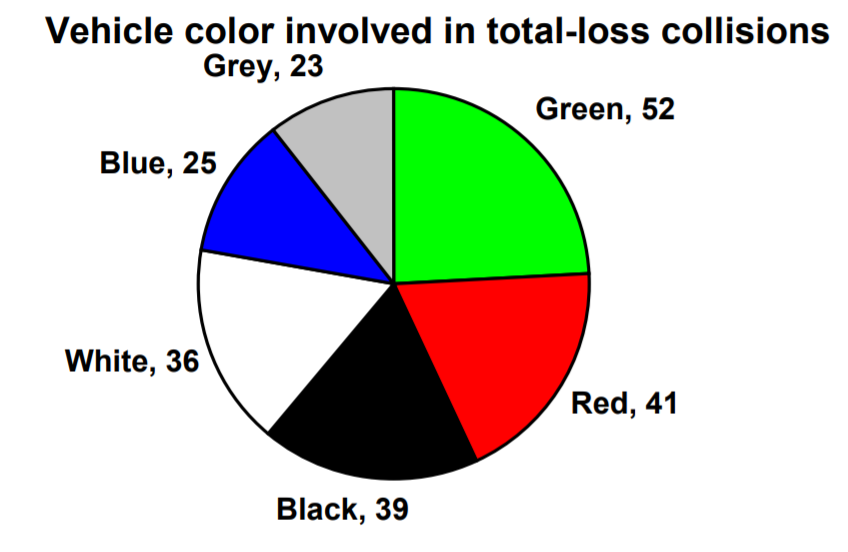
Los gráficos circulares a menudo pueden beneficiarse al incluir frecuencias o frecuencias relativas (porcentajes) en el gráfico junto a los cortes circulares. A menudo, tener los nombres de las categorías junto a los cortes circulares también hace que el gráfico sea más claro.
El gráfico circular de la derecha muestra el porcentaje de votantes que apoyan a cada candidato que se postula para un escaño en el senado local.
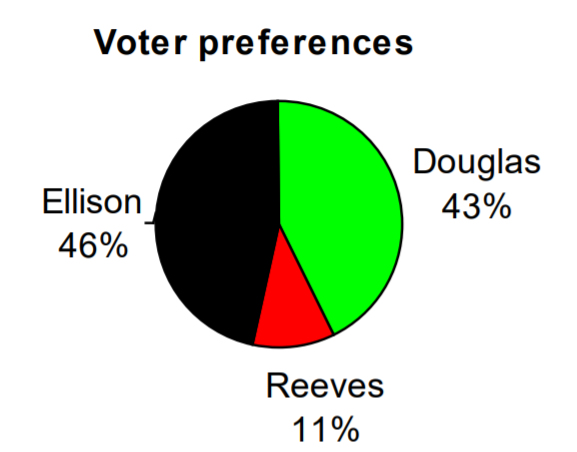
Si hay 20 mil votantes en el distrito, el gráfico circular muestra que alrededor del 11% de esos, alrededor de 2,200 votantes, apoyan a Reeves.
Los gráficos circulares se ven bien pero son más difíciles de dibujar a mano que los gráficos de barras ya que para dibujarlos con precisión necesitaríamos calcular el ángulo que cada cuña corta del círculo, luego medir el ángulo con un prolongador. Las computadoras son mucho más adecuadas para dibujar gráficos circulares. Programas de software comunes como Microsoft Word o Excel, OpenOffice.org Write o Calc, o Google Docs son capaces de crear gráficos de barras, gráficos circulares y otros tipos de gráficos. También existen numerosas herramientas en línea que pueden crear gráficas [2].
Cree un gráfico de barras y un gráfico circular para ilustrar las calificaciones en un examen de historia a continuación.
A: 12 alumnos,
B: 19 alumnos,
C: 14 alumnos,
D: 4 alumnos,
F: 5 alumnos
¡No te pongas elegante con las gráficas! La gente a veces agrega características a los gráficos que no ayudan a transmitir su información. Por ejemplo, los gráficos de barras tridimensionales como el que se muestra a continuación no suelen ser tan efectivos como sus contrapartes bidimensionales.
Aquí hay otra forma en que la imaginería puede llevar a problemas. En lugar de barras lisas, es tentador sustituir imágenes significativas. Este tipo de gráfica se llama pictograma.
Un pictograma es un gráfico estadístico en el que se pretende que el tamaño de la imagen represente las frecuencias o el tamaño de los valores que se están representando.
Un sindicato podría producir la gráfica a la derecha para mostrar la diferencia entre el salario promedio de gerente y el salario promedio del trabajador.

Al mirar la imagen, sería razonable adivinar que los salarios del gerente son 4 veces más grandes que los salarios de los trabajadores — el área de la bolsa se ve aproximadamente 4 veces más grande. No obstante, los salarios de los gerentes son de hecho sólo el doble que los salarios de los trabajadores, lo que se reflejó en la imagen al hacer que la bolsa de gerente sea el doble de alta.
Otra distorsión en los gráficos de barras resulta de establecer la línea base en un valor distinto de cero. La línea base es la parte inferior del eje vertical, representando el menor número de casos que podrían haber ocurrido en una categoría. Normalmente, este número debería ser cero.
Compare las dos gráficas a continuación que muestran el apoyo a los derechos de matrimonio entre personas del mismo sexo de una encuesta realizada en diciembre de 2008 [3]. La diferencia en la escala vertical en la primera gráfica sugiere una historia diferente a las verdaderas diferencias en porcentajes; la segunda gráfica hace que parezca que el doble de personas se oponen a los derechos matrimoniales que lo apoyan.
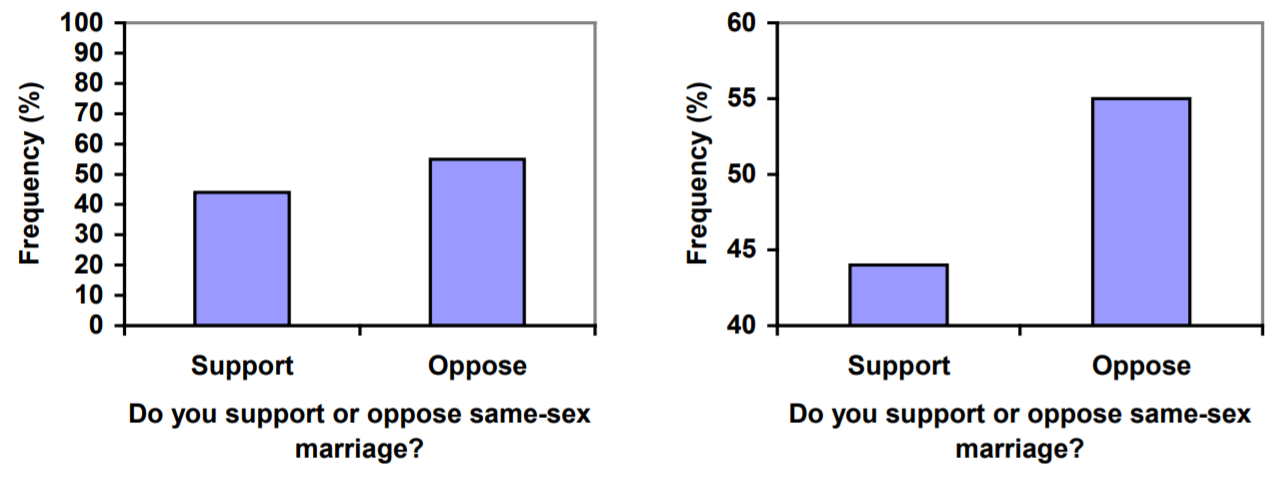
Se realizó una encuesta preguntando a la gente si estaban de acuerdo con las posiciones de los 4 candidatos a una oficina del condado. ¿El gráfico circular presenta una buena representación de estos datos? Explique.