9.2: Presentación gráfica de datos cuantitativos
- Page ID
- 112911
Los datos cuantitativos o numéricos también se pueden resumir en tablas de frecuencias.
Un profesor registra puntuaciones en un cuestionario de 20 puntos para los 30 alumnos de su clase. Los puntajes son
19 20 18 18 17 18 19 17 20 18 20 16 20 15 17 12 18 19 18 19 17 20 18 16 15 18 20 5 0 0
Estas puntuaciones podrían resumirse en una tabla de frecuencias agrupando valores similares:
| Score | Frecuencia |
|---|---|
| 0 | 2 |
| 5 | 1 |
| 12 | 1 |
| 15 | 2 |
| 16 | 2 |
| 17 | 4 |
| 18 | 8 |
| 19 | 4 |
| 20 | 6 |
Usando esta tabla, sería posible crear un gráfico de barras estándar a partir de este resumen, como hicimos para los datos categóricos:
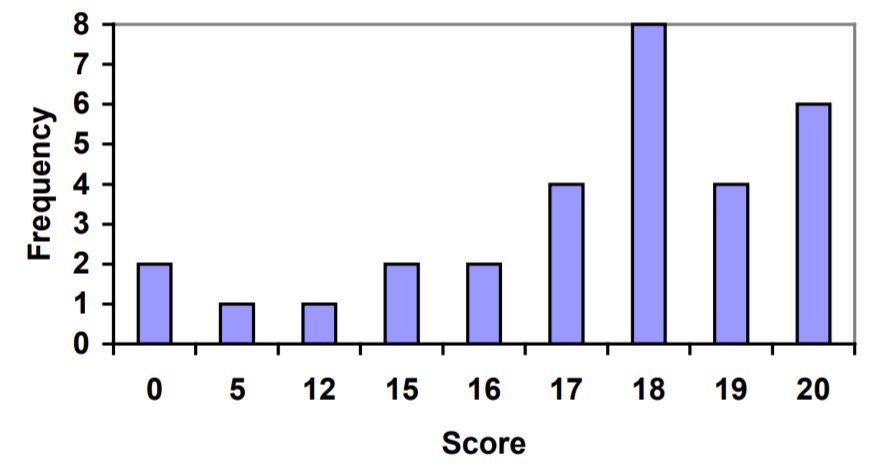
Sin embargo, dado que las puntuaciones son valores numéricos, este gráfico realmente no tiene sentido; las barras primera y segunda están separadas por cinco valores, mientras que las barras posteriores están separadas solo con un valor. Sería más correcto tratar el eje horizontal como una recta numérica. Este tipo de gráfica se denomina histograma.
Un histograma es una representación gráfica de datos cuantitativos. El eje horizontal es una recta numérica.
Para los valores anteriores, un histograma se vería así:
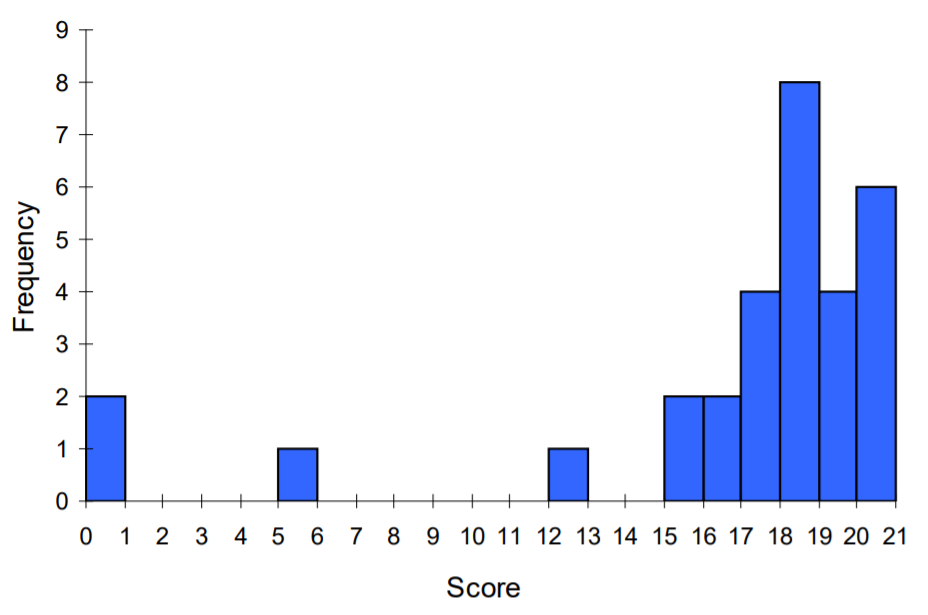
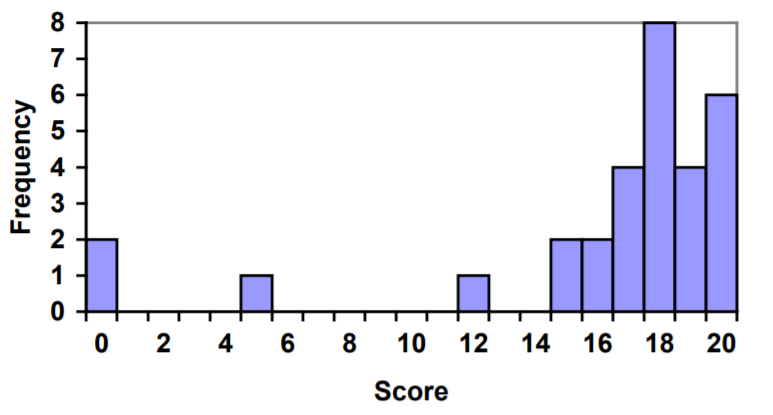Observe que, en el histograma, una barra representa valores en el eje horizontal desde el del lado izquierdo de la barra hasta, pero sin incluir, el valor en el lado derecho de la barra. Algunas personas optan por que las barras comiencen en\(\dfrac{1}{2}\) valores para evitar esta ambigüedad.
Desafortunadamente, no muchos paquetes de software comunes pueden graficar correctamente un histograma. Acerca de lo mejor que puedes hacer en Excel o Word es un gráfico de barras sin hueco entre las barras y espaciado agregado para simular un eje horizontal numérico.
Si tenemos un gran número de valores de datos ampliamente variables, crear una tabla de frecuencias que enumera todos los valores posibles como categoría conduciría a una tabla de frecuencias excepcionalmente larga, y probablemente no revelaría ningún patrón. Por esta razón, es común con los datos cuantitativos agrupar los datos en intervalos de clase.
Los intervalos de clase son agrupaciones de los datos. En general, definimos intervalos de clase para que
- Cada intervalo es igual en tamaño. Por ejemplo, si la primera clase contiene valores de 120-129, la segunda clase debe incluir valores de 130-139.
- Cada intervalo tiene un límite inferior y un límite superior, por ejemplo, para el intervalo 120-129, 120 es el límite inferior y 129 es el límite superior.
- El ancho de clase es la diferencia entre dos límites inferiores consecutivos.
- El ancho de clase es el mismo para cada intervalo en la tabla de frecuencias.
- Tenemos en algún lugar entre 5 y 20 clases, normalmente, dependiendo de la cantidad de datos con los que estamos trabajando.
Supongamos que hemos recolectado pesos de 100 sujetos masculinos como parte de un estudio de nutrición. Para nuestros datos de peso, tenemos valores que van desde un mínimo de 121 libras hasta un máximo de 263 libras, dando un lapso total de\(263-121 = 142\). Podríamos crear 7 intervalos con un ancho de alrededor de 20, 14 intervalos con un ancho de alrededor de 10, o algún punto intermedio. A menudo, tenemos que experimentar con algunas posibilidades para encontrar algo que represente bien los datos. Intentemos usar un ancho de intervalo de 15. Podríamos comenzar en 121, o en 120 ya que es un bonito número redondo.
| Intervalo | Frecuencia |
|---|---|
| 120-134 | 4 |
| 135-149 | 14 |
| 150-164 | 16 |
| 165-189 | 28 |
| 180-194 | 12 |
| 195-209 | 8 |
| 210-224 | 7 |
| 225-239 | 6 |
| 240-254 | 2 |
| 255-269 | 3 |
Observe, el ancho de clase es 15 desde\(150-135 = 15\)\(165-150 = 15\),, y así sucesivamente.
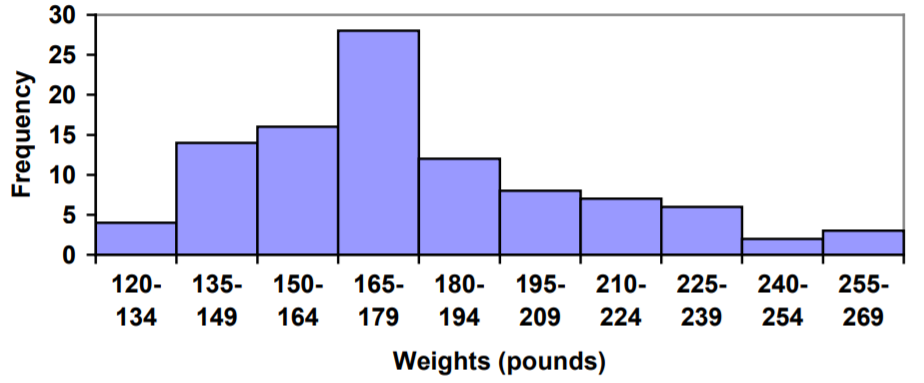
Un histograma de estos datos se vería así:
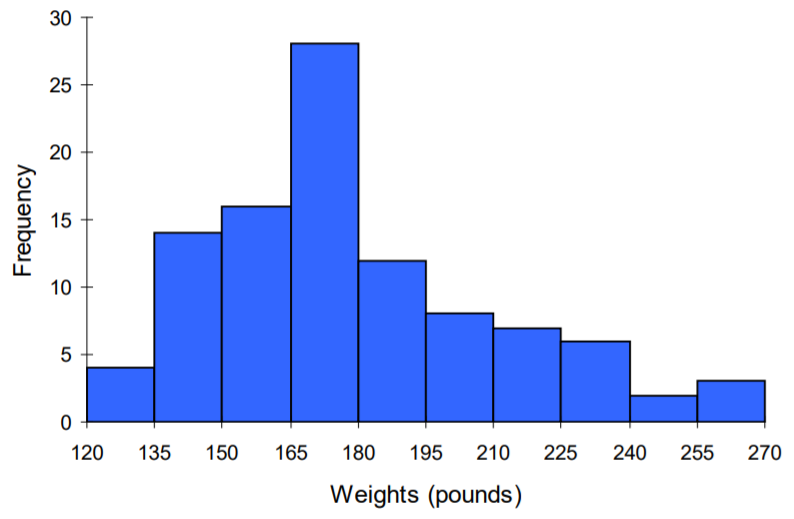
En muchos paquetes de software, puede crear una gráfica similar a un histograma poniendo los intervalos de clase como etiquetas en un gráfico de barras.
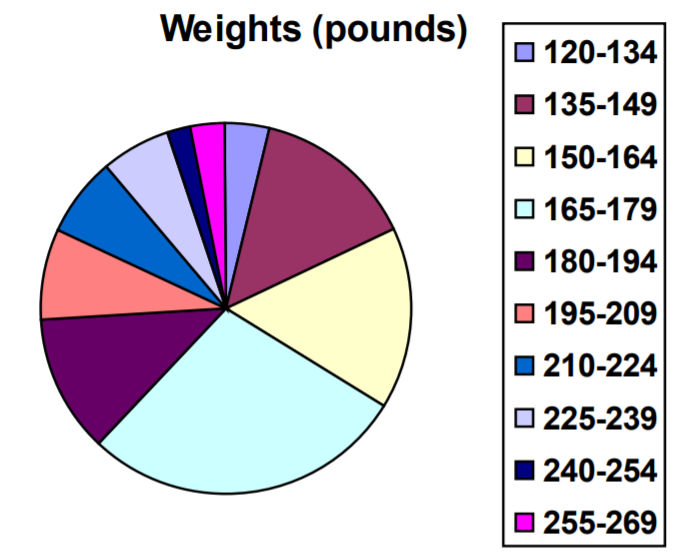
Otros tipos de gráficos, como los gráficos circulares, son posibles para los datos cuantitativos. La utilidad de los diferentes tipos de gráficos variará dependiendo del número de intervalos y del tipo de datos que se representen. Por ejemplo, un gráfico circular de nuestros datos de peso es difícil de leer debido a la cantidad de intervalos que usamos.
El costo total de los libros de texto para el término se recolectó de 36 estudiantes. Crear un histograma para estos datos.
$140 $160 $160 $165 $180 $220 $235 $240 $250 $260 $280 $285
$285 $290 $300 $300 $305 $310 $310 $315 $315 $320 $320
$330 $340 $345 $350 $355 $360 $360 $380 $395 $420 $460 $460
Al recolectar datos para comparar dos grupos, es deseable crear una gráfica que compare cantidades.
Los datos a continuación provinieron de una tarea en la que el objetivo es mover un mouse de computadora a un objetivo en la pantalla lo más rápido posible. En 20 de los ensayos, el objetivo era un rectángulo pequeño; en los otros 20, el objetivo era un rectángulo grande. En cada ensayo se registró el tiempo para alcanzar el objetivo.
| Intervalo (milisegundos) | Objetivo pequeño de frecuencia | Objetivo grande de frecuencia |
|---|---|---|
| 300-399 | 0 | 0 |
| 400-499 | 1 | 5 |
| 500-599 | 3 | 10 |
| 600-699 | 6 | 5 |
| 700-799 | 5 | 0 |
| 800-899 | 4 | 0 |
| 900-999 | 0 | 0 |
| 1000-1099 | 1 | 0 |
| 1100-1199 | 0 | 0 |
Una opción para representar estos datos sería un histograma comparativo o gráfico de barras, en el que las barras para el grupo objetivo pequeño y el grupo objetivo grande se colocan una al lado de la otra.
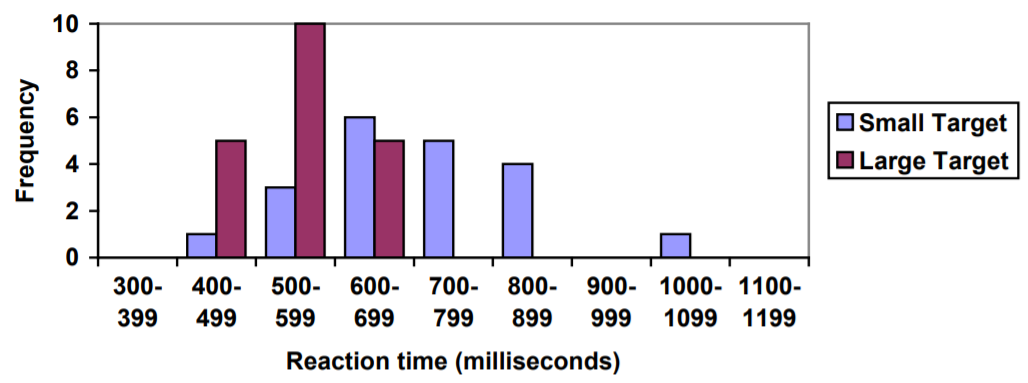
Una representación alternativa es un polígono de frecuencia. Un polígono de frecuencia comienza como un histograma, pero en lugar de dibujar una barra, se coloca un punto en el punto medio de cada intervalo a una altura igual a la frecuencia. El punto medio de un intervalo es
\[\dfrac{\text{lower limit}_2 - \text{lower limit}_1}{2} \nonumber \]
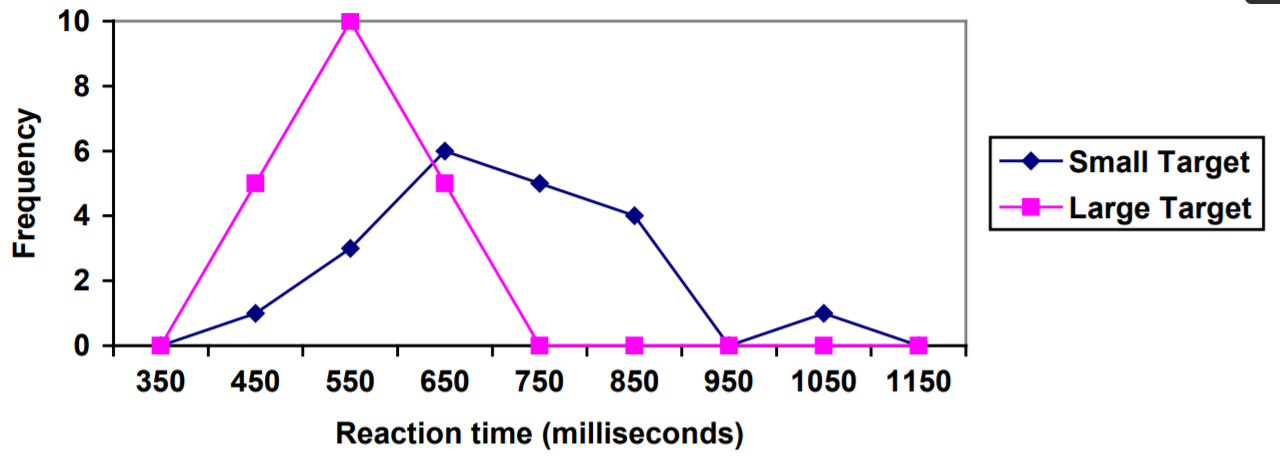
Normalmente, los puntos están conectados con líneas rectas para enfatizar la distribución de los datos.
Esta gráfica hace que sea más fácil ver que los tiempos de reacción fueron generalmente más cortos para el objetivo más grande, y que los tiempos de reacción para el objetivo más pequeño estaban más dispersos.
Resúmenes Numéricos de Datos
A menudo es deseable usar algunos números para resumir una distribución. Un aspecto importante de una distribución es donde se encuentra su centro. Se discuten primero las medidas de tendencia central. Un segundo aspecto de una distribución es lo dispersa que está. En otras palabras, cuánto varían entre sí los datos en la distribución. En la segunda sección se describen las medidas de variabilidad