9.4: Medidas de Variación
- Page ID
- 112906
Considera estos tres conjuntos de puntajes del cuestionario:
Sección A: 5 5 5 5 5 5 5 5 5 5
Sección B: 0 0 0 0 0 10 10 10 10 10
Sección C: 4 4 5 5 5 5 6 6 6
Los tres conjuntos de datos tienen una media de 5 y una mediana de 5, sin embargo, los conjuntos de puntuaciones son claramente bastante diferentes. En la sección A, todos tenían la misma puntuación; en la sección B, la mitad de la clase no obtuvo puntos y la otra mitad obtuvo una puntuación perfecta, asumiendo que se trataba de un cuestionario de 10 puntos. La sección C no fue tan consistente como la sección A, pero no tan variada como la sección B.
Además de la media y mediana, que son medidas del valor “típico” o “medio”, también necesitamos una medida de cuán “extendido” o variado está cada conjunto de datos.
Existen varias formas de medir esta “propagación” de los datos. El primero es el más simple y se llama el rango.
El rango es la diferencia entre el valor máximo y el valor mínimo del conjunto de datos.
Usando las puntuaciones del cuestionario de arriba,
Para la sección A, el rango es\(0\) ya que tanto el máximo como el mínimo son\(5\) y\(5 – 5 = 0\)
Para la sección B, el rango es\(10\) desde\(10 – 0 = 10\)
Para la sección C, el rango es\(2\) desde\(6 – 4 = 2\)
En el último ejemplo, el rango parece estar revelando cuán dispersos están los datos. Sin embargo, supongamos que agregamos una cuarta sección, la Sección D, con puntuaciones
0 5 5 5 5 5 5 5 5 5 10
Esta sección también tiene una media y mediana de 5. El rango es 10, sin embargo, este conjunto de datos es bastante diferente a la Sección B. Para iluminar mejor las diferencias, tendremos que recurrir a medidas de variación más sofisticadas.
La desviación estándar es una medida de variación basada en medir la distancia que cada valor de datos se desvía, o es diferente, de la media. Algunas características importantes:
- La desviación estándar siempre es positiva. La desviación estándar será cero si todos los valores de los datos son iguales, y se hará más grande a medida que los datos se desplieguen.
- La desviación estándar tiene las mismas unidades que los datos originales.
- La desviación estándar, al igual que la media, puede estar muy influenciada por valores atípicos.
Usando los datos de la sección D, podríamos calcular para cada valor de datos la diferencia entre el valor de datos y la media:
| Valor de datos | Desviación: Valor de datos - Media |
| 0 | 0-5 = -5 |
| 5 | 5-5 = 0 |
| 5 | 5-5 = 0 |
| 5 | 5-5 = 0 |
| 5 | 5-5 = 0 |
| 5 | 5-5 = 0 |
| 5 | 5-5 = 0 |
| 5 | 5-5 = 0 |
| 5 | 5-5 = 0 |
| 10 | 10-5 = 0 |
Nos gustaría tener una idea de la desviación “promedio” de la media, pero si encontramos el promedio de los valores en la segunda columna los valores negativos y positivos se cancelan entre sí (esto siempre sucederá), así que para evitar esto cuadramos cada valor en la segunda columna:
| Valor de datos | Desviación: Valor de datos - Media | (Desviación) 2 |
| 0 | 0-5 = -5 | (-5) 2 = 25 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 5 | 5-5 = 0 | 0 2 = 0 |
| 10 | 10-5 = 5 | (5) 2 = 25 |
Luego agregamos las desviaciones cuadradas hasta obtener\(25 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 25 = 50\). Ordinariamente, entonces dividiríamos por el número de puntajes\(n\),, (en este caso, 10) para encontrar la media de las desviaciones. Pero solo hacemos esto si el conjunto de datos representa una población; si el conjunto de datos representa una muestra (como casi siempre lo hace), en cambio dividimos por\(n - 1\) (en este caso,\(10 - 1 = 9\)) [4].
Entonces, en nuestro ejemplo, tendríamos\(\dfrac{50}{10} = 5\) si la sección D representa una población y\(\dfrac{50}{9} =\) aproximadamente\(5.56\) si la sección D representa una muestra. Estos valores (\(5\)y\(5.56\)) se denominan, respectivamente, la varianza poblacional y la varianza muestral para la sección D.
La varianza puede ser un concepto estadístico útil, pero tenga en cuenta que las unidades de varianza en esta instancia serían puntos al cuadrado ya que cuadramos todas las desviaciones. ¿Qué son los puntos-cuadrados? Buena pregunta. Preferiríamos tratar con las unidades con las que empezamos (puntos en este caso), así que para volver a convertir tomamos la raíz cuadrada y obtenemos:
\(\text{Population Standard Deviation } = \sqrt{\dfrac{50}{10}} = \sqrt{5} ≈ 2.2\)
\(\text{Sample Standard Deviation } = \sqrt{\dfrac{50}{9}} ≈ 2.4\)
¿Qué dice esto de la sección D? Podemos decir que el puntaje promedio fue de 5 dar o tomar 2.4. La parte de “dar o tomar” es el prefijo para la desviación estándar. En el último capítulo, discutimos más sobre la relación entre el promedio y la desviación estándar. Por ahora, podemos interpretar los resultados como “el promedio es ________ dar o tomar [desviación estándar]”.
Si no estamos seguros de si el conjunto de datos es una muestra o una población, generalmente asumiremos que es una muestra, y redondearemos las respuestas a un decimal más que los datos originales, como hemos hecho anteriormente.
- Encuentra la desviación de cada dato de la media. En otras palabras, restar la media del valor de los datos.
- Cuadrando cada desviación.
- Añadir las desviaciones al cuadrado.
- Dividir por\(n\), el número de valores de datos, si los datos representan una población completa; dividir por\(n – 1\) si los datos son de una muestra. (Este resultado es la varianza de la muestra.)
- Calcular la raíz cuadrada del resultado. (Este resultado es la desviación estándar.)
Calculando la desviación estándar para la Sección B anterior, primero calculamos que la media es 5. El uso de una tabla puede ayudar a realizar un seguimiento de sus cálculos para la desviación estándar:
| Valor de datos | Desviación: Valor de datos - Media | (Desviación) 2 |
| 0 | 0-5 = -5 | (-5) 2 = 25 |
| 0 | 0-5 = -5 | (-5) 2 = 25 |
| 0 | 0-5 = -5 | (-5) 2 = 25 |
| 0 | 0-5 = -5 | (-5) 2 = 25 |
| 0 | 0-5 = -5 | (-5) 2 = 25 |
| 10 | 10-5 = 5 | (5) 2 = 25 |
| 10 | 10-5 = 5 | (5) 2 = 25 |
| 10 | 10-5 = 5 | (5) 2 = 25 |
| 10 | 10-5 = 5 | (5) 2 = 25 |
| 10 | 10-5 = 5 | (5) 2 = 25 |
Suponiendo que estos datos representan una población, agregaremos las desviaciones cuadradas, dividiremos por 10, el número de valores de datos y calcularemos la raíz cuadrada:
\(\sqrt{\dfrac{25 + 25 + 25 + 25 + 25 + 25 + 25 + 25 + 25 + 25}{10}} = \sqrt{\dfrac{250}{10}} = 5\)
Observe que la desviación estándar de este conjunto de datos es mucho mayor que la de la sección D ya que los datos de este conjunto están más dispersos. Así, el puntaje promedio fue de 5 dar o tomar 5.
A modo de comparación, las desviaciones estándar de las cuatro secciones son
| Sección A: 5 5 5 5 5 5 5 5 5 5 | Desviación estándar: 0 |
| Sección B: 0 0 0 0 0 10 10 10 10 10 | Desviación estándar: 5 |
| Sección C: 4 4 5 5 5 5 6 6 6 | Desviación estándar: 0.8 |
| Sección D: 0 5 5 5 5 5 5 5 5 5 10 | Desviación estándar: 2.2 |
El precio de un frasco de mantequilla de maní en 5 tiendas fue: $3.29, $3.59, $3.79, $3.75, y $3.99. Encuentra la desviación estándar de los precios.
Cuando la desviación estándar es una medida de variación basada en la media, los cuartiles se basan en la mediana.
Los cuartiles son valores que dividen los datos en trimestres.
El primer cuartil (Q 1) es el valor de manera que 25% de los valores de datos están por debajo de él; el tercer cuartil (Q 3) es el valor de manera que 75% de los valores de datos están por debajo de él. Es posible que hayas adivinado que el segundo cuartil es lo mismo que la mediana, ya que la mediana es el valor por lo que el 50% de los valores de los datos están por debajo de él.
Esto divide los datos en trimestres; el 25% de los datos se encuentra entre el mínimo y Q 1, el 25% está entre Q 1 y la mediana, el 25% está entre la mediana y Q 3, y el 25% está entre Q 3 y el valor máximo
Si bien los cuartiles no son un resumen de variación de 1 número como la desviación estándar, los cuartiles se utilizan con los valores de mediana, mínimo y máximo para formar un resumen de 5 números de los datos.
El resumen de cinco números toma esta forma
Mínimo, Q 1, Mediana, Q 3, Máximo
Para encontrar el primer cuartil, necesitamos encontrar el valor de los datos para que el 25% de los datos estén por debajo de él. Si\(n\) es el número de valores de datos, calculamos un localizador encontrando 25% de\(n\). Si este localizador es un valor decimal, redondeamos y encontramos el valor de los datos en esa posición. Si el localizador es un número entero, encontramos la media del valor de datos en esa posición y el siguiente valor de datos. Esto es idéntico al proceso que usamos para encontrar la mediana, excepto que usamos 25% de los valores de datos en lugar de la mitad de los valores de datos como localizador.
- Comience ordenando los datos de menor a mayor.
- Calcular el localizador:\(L = 0.25n\).
- Si\(L\) es un valor decimal:
- Redondear hasta\(L+\)
- Utilice el valor de los datos en la\(L+^{\text{th}}\) posición.
Si\(L\) es un número entero:
- Encuentra la media de los valores de datos en las\(L+1^{\text{th}}\) posiciones\(L^{\text{th}}\) y.
Utilice el mismo procedimiento que para Q 1, pero con localizador:\(L = 0.75n\)
Veamos algunos ejemplos. También podemos calcular el resumen de 5 números en calculadoras, o algún software científico como Excel, Minitab, o R. Sin embargo, en este curso, solo nos mojamos los pies con las estadísticas, por lo que podemos calcular estos valores rápidamente a mano.
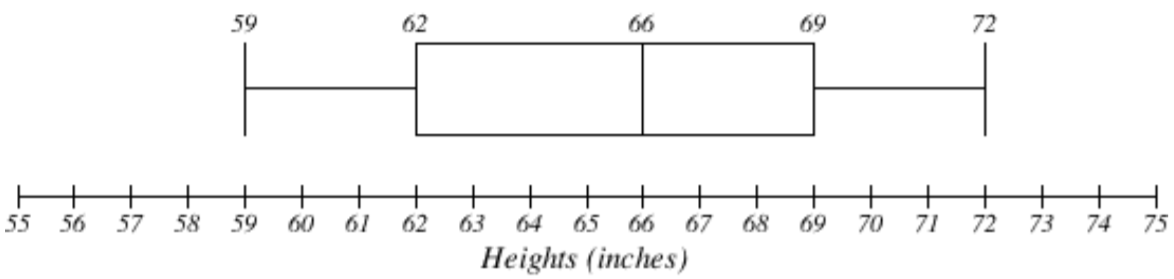
Supongamos que hemos medido 9 hembras y sus alturas (en pulgadas), ordenadas de menor a mayor son:
59 60 62 64 66 67 69 70 72
Para encontrar el primer cuartil primero calculamos el localizador: 25% de 9 es\(L = 0.25(9) = 2.25\). Dado que este valor no es un número entero, redondeamos hasta 3. El primer cuartil será el tercer valor de datos: 62 pulgadas. Podemos decir que el 25% de las hembras son menores de 62 pulgadas y el otro 75% es más alto que 62 pulgadas.
Para encontrar el tercer cuartil, nuevamente calculamos el localizador: 75% de 9 es\(0.75(9) = 6.75\). Dado que este valor no es un número entero, redondeamos hasta 7. El tercer cuartil será el séptimo valor de datos: 69 pulgadas. Podemos decir que 75% de las hembras son más cortas que 69 pulgadas y el otro 25% es más alto que 69 pulgadas.
Supongamos que habíamos medido 8 hembras y sus alturas (en pulgadas), ordenadas de menor a mayor son:
59 60 62 64 66 67 69 70
Para encontrar el primer cuartil primero calculamos el localizador: 25% de 8 es\(L = 0.25(8) = 2\). Dado que este valor es un número entero, encontraremos la media de los valores de datos 2 y 3 rd:\(\dfrac{(60+62)}{2} = 61\), por lo que el primer cuartil es de 61 pulgadas. Podemos decir que el 25% de las hembras son menores de 61 pulgadas y el otro 75% es más alto que 61 pulgadas.
El tercer cuartil se calcula de manera similar, utilizando 75% en lugar de 25%. \(L = 0.75(8) = 6\). Se trata de un número entero, por lo que encontraremos la media de los valores de los datos 6º y 7º:\(\dfrac{(67+69)}{2} = 68\), así que Q 3 es de 68 pulgadas. Podemos decir que el 75% de las hembras son menores de 68 pulgadas y el otro 25% es más alto que 68 pulgadas.
Tenga en cuenta que la mediana podría calcularse de la misma manera, usando el 50% o un localizador de\(L = 0.5n\)
El resumen de 5 números combina el primer y tercer cuartil con los valores mínimo, mediano y máximo.
En el ejemplo con una muestra de 9 hembras, la mediana es 66, la mínima es 59, y la máxima es 72. Por lo tanto, el resumen de 5 números es:
59, 62, 66, 69, 72.
En el ejemplo con una muestra de 8 hembras, la mediana es 65, la mínima es 59, y la máxima es 70, por lo que el resumen de 5 números es:
59, 61, 65, 68, 70.
Volviendo a nuestros datos de puntuación del cuestionario. En cada caso, el primer localizador de cuartil es 0.25 (10) = 2.5, por lo que el primer cuartil será el 3er valor de datos, y el tercer cuartil será el octavo valor de datos. Creando los resúmenes de cinco números:
| Sección y Datos | Resumen de 5 números |
| Sección A: 5 5 5 5 5 5 5 5 5 5 | Desviación estándar: 0 |
| Sección B: 0 0 0 0 0 10 10 10 10 10 | Desviación estándar: 5 |
| Sección C: 4 4 5 5 5 5 6 6 6 | Desviación estándar: 0.8 |
| Sección D: 0 5 5 5 5 5 5 5 5 5 10 | Desviación estándar: 2.2 |
Por supuesto, con un conjunto de datos relativamente pequeño, encontrar un resumen de cinco números es un poco tonto, ya que el resumen contiene casi tantos valores como los datos originales.
El costo total de los libros de texto para el término se recolectó de 36 estudiantes. Encuentra el resumen de 5 números de estos datos.
$140 $160 $160 $165 $180 $220 $235 $240 $250 $260 $280 $285
$285 $290 $300 $300 $305 $310 $310 $315 $315 $320 $320
$330 $340 $345 $350 $355 $360 $360 $380 $395 $420 $460 $460
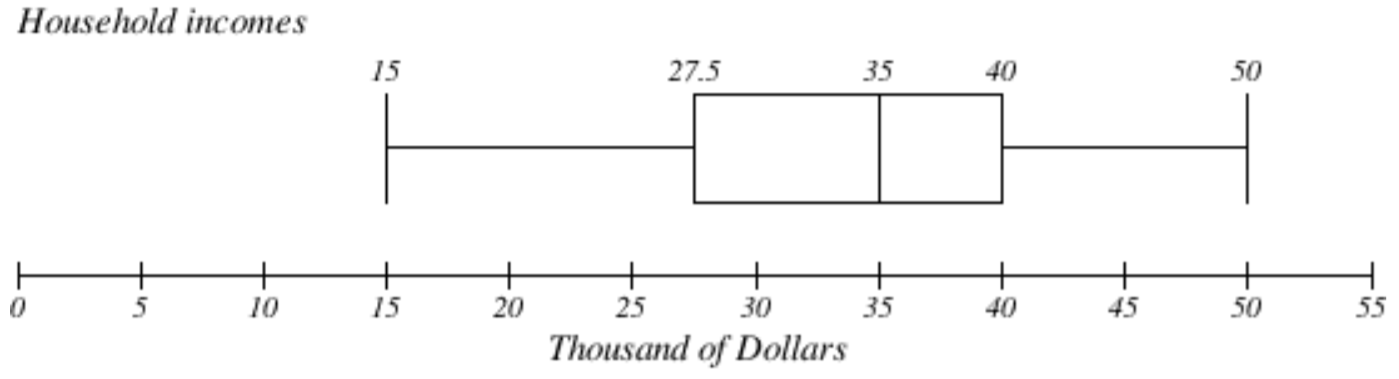
Volviendo a los datos de ingresos de los hogares de antes, crear el resumen de cinco números.
| Ingresos (miles de dólares) | Frecuencia |
| $15 | 6 |
| $20 | 8 |
| $25 | 11 |
| $30 | 17 |
| $35 | 19 |
| $40 | 20 |
| $45 | 12 |
| $50 | 7 |
Al sumar las frecuencias, podemos ver que hay 100 valores de datos representados en la tabla. En el Ejemplo 9.3.7, encontramos que la mediana fue de $35 mil. Podemos ver en la tabla que el ingreso mínimo es de $15 mil, y el máximo es de $50 mil.
Para encontrar Q 1, calculamos el localizador:\(L = 0.25(100) = 25\). Este es un número entero, por lo que Q 1 será la media de los valores de datos 25 º y 26 º.
Contando en los datos como lo hacíamos antes,
Hay 6 valores de datos de $15, por lo que los Valores 1 a 6 son $15 mil
Los siguientes 8 valores de datos son $20, por lo que los Valores 7 a\((6+8)=14\) son $20 mil
Los siguientes 11 valores de datos son $25, por lo que los Valores 15 a\((14+11)=25\) son $25 mil
Los siguientes 17 valores de datos son $30, por lo que los Valores 26 a\((25+17)=42\) son $30 mil
El 25 º valor de datos es de 25 mil dólares, y el 26 º valor de datos es de $30 mil, por lo que Q 1 será la media de estos:\(\dfrac{(25 + 30)}{2} = $27.5\) mil.
Para encontrar Q 3, calculamos el localizador:\(L = 0.75(100) = 75\). Este es un número entero, por lo que Q 3 será la media de los valores de datos 75 º y 76 º. Continuando nuestro conteo desde antes,
Los siguientes 19 valores de datos son $35, por lo que los Valores 43 a\((42+19)=61\) son $35 mil
Los siguientes 20 valores de datos son $40, por lo que los Valores 61 a\((61+20)=81\) son $40 mil
Tanto los valores de los datos 75 y 76 º se encuentran en este grupo, por lo que Q 3 será de $40 mil.
Al juntar estos valores en un resumen de cinco números, obtenemos: 15, 27.5, 35, 40, 50.
Tenga en cuenta que el resumen de 5 números divide los datos en cuatro intervalos, cada uno de los cuales contendrá alrededor del 25% de los datos. En el ejemplo anterior, alrededor del 25% de los hogares tienen ingresos entre $40 mil y $50 mil. Para visualizar datos, hay una representación gráfica de un resumen de 5 números llamado diagrama de caja, o gráfico de caja y bigotes.
Para visualizar datos, hay una representación gráfica de un resumen de 5 números llamado diagrama de caja, o gráfico de caja y bigotes.
Un diagrama de caja es una representación gráfica de un resumen de cinco números.
Para crear una gráfica de caja, primero se dibuja una recta numérica con marcas de selección equidistantes. Se dibuja una caja desde el primer cuartil hasta el tercer cuartil, y se dibuja una línea a través de la caja en la mediana. Los “bigotes” se extienden a los valores mínimo y máximo.
La gráfica de cuadro a continuación se basa en el resumen de 5 números de la muestra de 9 alturas femeninas:
59, 62, 66, 69, 72
El diagrama de caja a continuación se basa en el resumen de 5 números de la muestra de los ingresos de los hogares:
15, 27.5, 35, 40, 50
Crea una gráfica de caja basada en los datos de precios del libro de texto del último Pruébalo ahora.
Las parcelas de caja son particularmente útiles para comparar datos de dos poblaciones o muestras. De hecho, cuando tenemos dos muestras para comparar, siempre se prefiere usar parcelas de caja.
A continuación se muestra la trama de caja de tiempos de servicio para dos restaurantes de comida rápida.
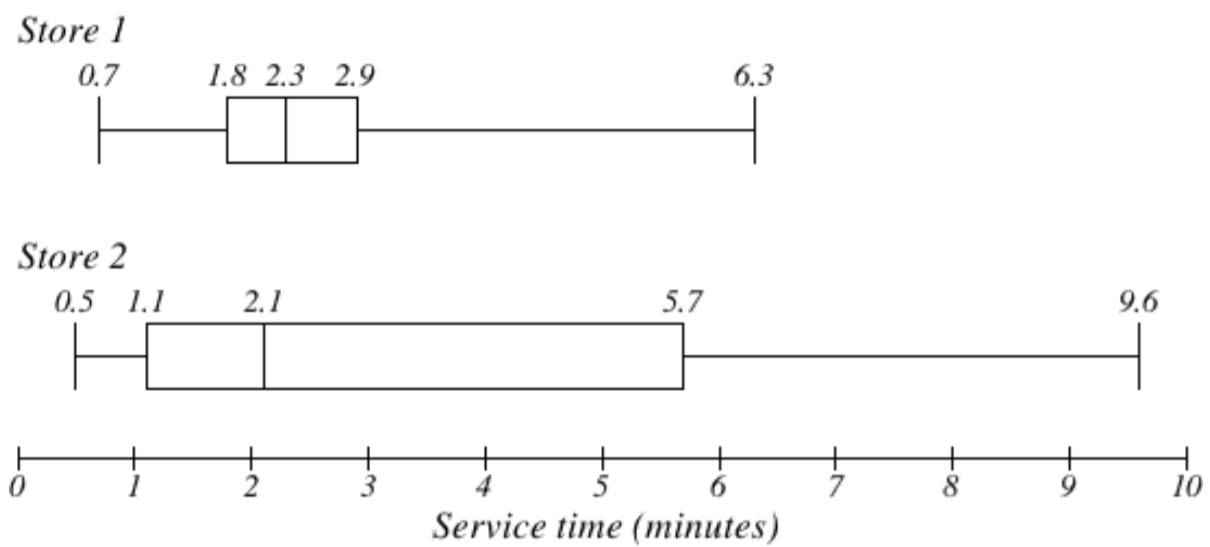
Mientras que la tienda 2 tuvo una mediana de tiempo de servicio ligeramente más corta (2.1 minutos vs. 2.3 minutos), la tienda 2 es menos consistente, con una distribución más amplia de los datos.
En la tienda 1, 75% de los clientes fueron atendidos dentro de 2.9 minutos, mientras que en la tienda 2, 75% de los clientes fueron atendidos dentro de 5.7 minutos.
¿A qué tienda deberías ir a toda prisa? Eso depende de tus opiniones sobre la suerte — 25% de los clientes de la tienda 2 tuvieron que esperar entre 5.7 y 9.6 minutos.
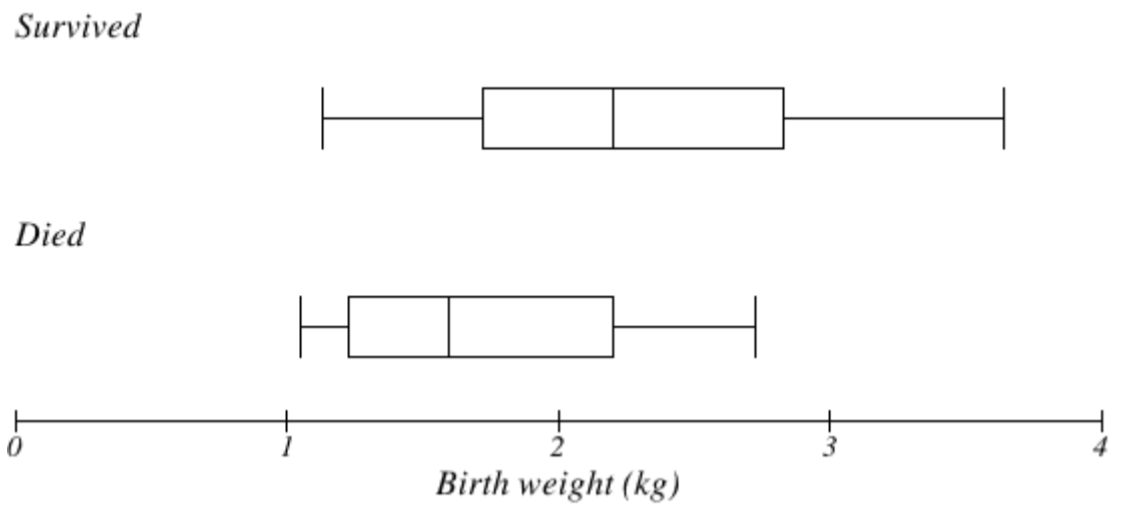
La gráfica de caja a continuación se basa en el peso al nacer de los recién nacidos con síndrome de dificultad respiratoria idiopática grave (SIRDS) [5]. La parcela de caja se separa para mostrar los pesos al nacer de los recién nacidos que sobrevivieron y los que no.
Al comparar los dos grupos, la gráfica de caja revela que los pesos al nacer de los recién nacidos que murieron parecen ser, en general, menores que los pesos de los recién nacidos que sobrevivieron. De hecho, podemos ver que la mediana de peso al nacer de los infantes que sobrevivieron es el mismo que el tercer cuartil de los infantes que murieron.
De igual manera, podemos ver que el primer cuartil de los sobrevivientes es mayor que la mediana del peso de los que murieron, lo que significa que más del 75% de los sobrevivientes tuvieron un peso al nacer mayor que el peso medio al nacer de los que murieron.
Al observar el valor máximo para los que murieron y el tercer cuartil de los sobrevivientes, podemos ver que más del 25% de los sobrevivientes tuvieron pesos al nacer más altos que el infante más pesado que murió.
La trama de caja nos da una manera rápida, aunque informal, de determinar que el peso al nacer está muy probablemente vinculado a la supervivencia de los infantes con SIRDS.
1.
2. Si bien el gráfico circular representa con precisión el tamaño relativo de las personas que están de acuerdo con cada candidato, el gráfico es confuso, ya que generalmente los porcentajes en un gráfico circular representan el porcentaje del pastel que representa la porción.
3. Usando intervalos de clase de tamaño 55, podemos agrupar nuestros datos en seis intervalos:
| Intervalo de costo | Frecuencia |
| 140-194 | 5 |
| $195-249 | 3 |
| $250-304 | 9 |
| $305-359 | 12 |
| $360-414 | 4 |
| $415-469 | 3 |
Podemos usar la distribución de frecuencias para generar el histograma.
4. Sumando los precios y dividiendo por 5 obtenemos el precio medio: $3.682
5. Primero ponemos los datos en orden: $3.29, $3.59, $3.75, $3.79, $3.99. Dado que hay un número impar de datos, la mediana será el valor medio, $3.75.
6. Hay 23 valoraciones.
a. La media es\(\dfrac{(1 \cdot 4) + (2 \cdot 8) + (3 \cdot 7) + (4 \cdot 3) + (5 \cdot 1)}{23} ≈ 2.5\)
b. Hay 23 valores de datos, por lo que la mediana será el 12 º valor de datos. Las calificaciones de 1 son los primeros 4 valores, mientras que una calificación de 2 son los siguientes 8 valores, por lo que el 12 º valor será una calificación de 2. La mediana es 2.
c. El modo es la calificación más frecuente. La clasificación de modo es 2.
7. Anteriormente encontramos que la media de los datos fue de $3.682.
| Valor de datos | Desviación: Valor de datos - Media | Desviación Cuadrada |
| 3.29 | 3.29 — 3.682 = -0.391 | 0.153664 |
| 3.59 | 3.59 — 3.682 = -0.092 | 0.008464 |
| 3.79 | 3.79 — 3.682 = 0.108 | 0.011664 |
| 3.75 | 3.75 — 3.682 = 0.068 | 0.004624 |
| 3.99 | 3.99 — 3.682 = 0.308 | 0.094864 |
Estos datos son de una muestra, por lo que agregaremos las desviaciones cuadradas, dividiremos por 4, el número de valores de datos menos 1, y calcularemos la raíz cuadrada:
\(\sqrt{\dfrac{0.153664 + 0.008464 + 0.011664 + 0.004624 + 0.094864}{4}} ≈ $0.261\)
Así, el precio promedio de la mantequilla de maní es de $3.68 dar o tomar $0.26.
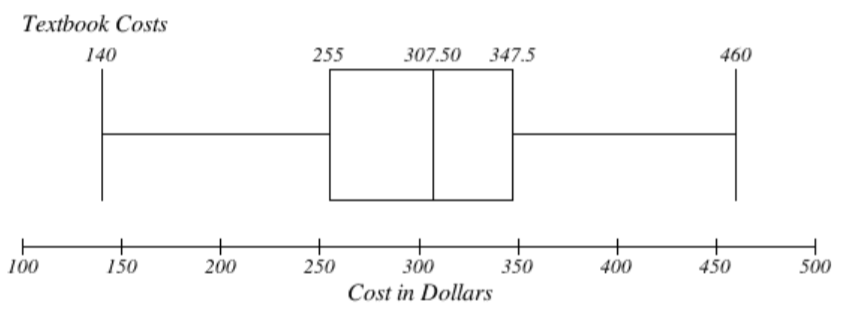
8. Los datos ya están en orden, así que no necesitamos ordenarlos primero. El valor mínimo es de $140 y el máximo es de $460.
Hay 36 valores de datos así\(n = 36\). \(\dfrac{n}{2} = 18\), que es un número entero, por lo que la mediana es la media de los valores de datos 18 y 19 º, 305 y 310 dólares. La mediana es de 307.50 dólares.
Para encontrar el primer cuartil, calculamos el localizador,\(L = 0.25(36) = 9\). Dado que se trata de un número entero, sabemos que Q 1 es la media de los valores de datos 9º y 10º, $250 y $260. Q 1 = 255$.
Para encontrar el tercer cuartil, calculamos el localizador,\(L = 0.75(36) = 27\). Dado que se trata de un número entero, sabemos que Q 3 es la media de los valores de los datos 27 y 28, 345 y 350 dólares. Q 3 = 347.50$.
El resumen número 5 de estos datos es: $140, $255, $307.50, $347.50, $460
9. Costos de boxplot de libros de texto:
