1.4: ¡Cuidado con los Patrones!
- Page ID
- 112774
La estrategia “Look for Patterns” puede ser particularmente atractiva, ¡pero hay que tener cuidado! No olvides la parte “y Explica” de la estrategia. No todos los patrones son obvios, y no todos continuarán.
Comienza con un círculo.

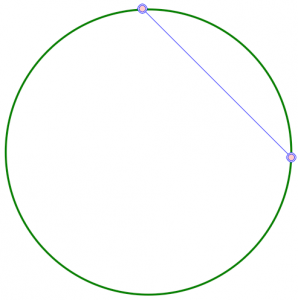
Si pongo dos puntos en el círculo y los conecto, la línea divide el círculo en dos piezas.
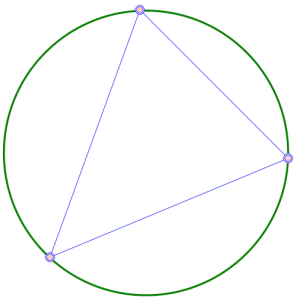
Si pongo tres puntos en el círculo y conecto cada par de puntos, las líneas divide el círculo en cuatro piezas.
Supongamos que pones cien puntos en un círculo y conectas cada par de puntos, es decir, cada punto está conectado a otros 99 puntos. ¿Cuántas piezas conseguirás? Las líneas pueden cruzarse entre sí, pero supongamos que los puntos se eligen para que tres o más líneas nunca se encuentren en un solo punto.
Después de haber trabajado en el problema por su cuenta por un tiempo, hable a través de sus ideas con un compañero (aunque no lo haya resuelto). ¿Qué estrategias probaste? ¿Qué averiguaste? ¿Qué preguntas aún tienes?
La forma natural de trabajar en este problema es usar números más pequeños de puntos y buscar un patrón, ¿verdad? Si aún no lo has hecho, pruébalo. ¿Cuántas piezas cuando tienes cuatro puntos? ¿Cinco puntos? ¿Cómo describirías el patrón?
Ahora prueba con seis puntos. Querrás dibujar un círculo grande y espaciar los seis puntos para que tu conteo sea más fácil. Después, cuente cuidadosamente cuántas piezas obtiene. Probablemente sea una buena idea trabajar con un compañero para que puedan verificar el trabajo del otro. Asegúrate de contar cada pieza una vez y no contar ninguna pieza dos veces. ¿Cómo puedes estar seguro de que haces eso?
¿Te sorprendió? Para los primeros varios pasos, parece ser el caso de que cuando agregas un punto dupliques el número de piezas. Pero eso significaría que para seis puntos, deberías obtener 32 piezas, y solo obtienes 30 o 31, dependiendo de cómo estén dispuestos los puntos. No importa lo que hagas, no puedes conseguir 32 piezas. El patrón simplemente no se sostiene.
A los matemáticos les encanta buscar patrones y encontrarlos. Nos emocionamos con los patrones. ¡Pero también somos muy escépticos de los patrones! Si no podemos explicar por qué ocurriría un patrón, entonces no estamos dispuestos a simplemente creerlo.
Por ejemplo, si mi patrón numérico empieza: 2, 4, 8,... Puedo encontrar muchas maneras de continuar con el patrón, cada una de las cuales tiene sentido en algunos contextos. Aquí hay algunas posibilidades:
- 2, 4, 8, 2, 4, 8, 2, 4, 8, 2, 4, 8,...
Este es un patrón repetitivo, recorriendo los números 2, 4, 8 y luego comenzando de nuevo con 2.
- 2, 4, 8, 32, 256, 8192,...
Para obtener el siguiente número, multiplique los dos números anteriores juntos.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,...
- 2, 4, 8, 14, 22, 32, 44, 58, 74...
- Para los dos últimos patrones anteriores, describa en palabras cómo se está creando la secuencia numérica.
- Encuentra al menos otras dos formas de continuar la secuencia 2, 4, 8,.. que se ve diferente a todas las que has visto hasta ahora. Escribe tu regla en palabras, y escribe los siguientes cinco términos de la secuencia numérica.
Entonces, ¿cómo puedes estar seguro de que tu patrón se ajusta al problema? ¡Tienes que atarlos juntos! ¿Recuerdas el problema de “Cuadrados en un tablero de ajedrez”? Es posible que hayas notado un patrón como este:
Si el tablero de ajedrez tiene 5 cuadrados en un lado, entonces hay
- 5 × 5 = 25 cuadrados de tamaño 1 × 1.
- 4 × 4 = 16 cuadrados de tamaño 2 × 2.
- 3 × 3 = 9 cuadrados de lado 3 × 3.
- 2 × 2 = 4 cuadrados de tamaño 4 × 4.
- 1 × 1 = 1 cuadrados de tamaño 5 × 5.
Así que hay un total de
\[1^{2} + 2^{2} + 3^{2} + 4^{2} + 5^{2} = 55 \nonumber \]
cuadrados en un tablero de ajedrez de 5 × 5. Probablemente puedas adivinar cómo continuar el patrón a cualquier tabla de tamaño, pero ¿cómo puedes estar absolutamente seguro de que el patrón continúa de esta manera? ¿Y si esto es como “Puntos en un Círculo”, y el patrón obvio se descompone después de unos pasos? Hay que atar el patrón al problema, para que quede claro por qué el patrón debe continuar de esa manera.
El primer paso para explicar un patrón es escribirlo claramente. Esto nos lleva a otra estrategia de resolución de problemas.
Estrategia de Resolución de Problemas 11 (¡Usa una Variable!).
Una de las herramientas más poderosas que tenemos es el uso de una variable. Si te encuentras haciendo cálculos en cosas como “el número de cuadrados” o “el número de puntos”, ¡dale un nombre a esas cantidades! Se vuelve mucho más fácil trabajar con ellos.
Por ahora, solo trabaja en describir el patrón con variables.
- Quédate con un tablero de ajedrez de 5 × 5 por ahora, y considera un pequeño cuadrado de tamaño k × k. Describe el patrón: ¿Cuántos cuadrados de tamaño k × k caben en un tablero de ajedrez de tamaño 5 × 5?
- ¿Y si el tablero de ajedrez es más grande? Con base en el patrón anterior, ¿cuántos cuadrados de tamaño k × k deben caber en un tablero de ajedrez de tamaño 10 × 10?
- ¿Y si no sabes qué tan grande es el tablero de ajedrez? Con base en el patrón anterior, ¿cuántos cuadrados de tamaño k × k deben caber en un tablero de ajedrez de tamaño n × n?
Ahora viene la parte dura: explicar el patrón. Centrémonos en una placa de 8 × 8. Ya que mide 8 cuadrados en cada lado, podemos ver que obtenemos 8× 8 = 64 cuadrados de tamaño 1× 1. Y como solo hay una sola tabla, obtenemos solo un cuadrado de tamaño 8 × 8. Pero, ¿qué pasa con todos los tamaños intermedios?
Utilizando como modelo el video Tablero de Ajedrez del capítulo anterior, trabaja con un compañero para explicar cuidadosamente por qué el número de 3 × 3 cuadrados será de 6 · 6 = 36, y por qué el número de 4 × 4 cuadrados será de 5 · 5 = 25.
Hay muchas explicaciones distintas a las que se encuentran en el video. Intenta encontrar tu propia explicación.
Así es como podría ser una justificación final (vea el video del Tablero de Ajedrez como ejemplo concreto de esta solución):
- Solución (Patrón de Tablero de Ajedrez).
-
Deja n ser el lado del tablero de ajedrez y deja que k sea el lado de la plaza. Si el cuadrado va a encajar en el tablero de ajedrez en absoluto, debe ser cierto que k ≤ n. De lo contrario, la plaza es demasiado grande.
Si pongo el cuadrado k × k en la esquina superior izquierda del tablero de ajedrez, ocupa k espacios cruzados y hay (n — k) espacios a la derecha del mismo. Así puedo deslizar el cuadrado k × k hacia la derecha (n — k) veces, hasta que llegue a la esquina superior derecha del tablero de ajedrez. El cuadrado se encuentra en (n — k + 1) diferentes posiciones, contando la posición inicial.
Si muevo el cuadrado k × k de nuevo a la esquina superior izquierda, puedo desplazarlo una fila hacia abajo y repetir todo el proceso nuevamente. Como hay (n — k) filas debajo del cuadrado, puedo desplazarlo hacia abajo (n — k) veces hasta que llegue a la fila inferior. Esto hace (n — k + 1) filas totales por las que se mueve el cuadrado, contando la fila superior.
Entonces, hay (n — k + 1) filas con (n — k + 1) cuadrados en cada fila. Eso hace (n — k + 1) 2 cuadrados totales.
Así, la solución es la suma de (n — k + 1) 2 para todos k ≤ n. En símbolos:
\[\text{number of squares on an n} \times \text{n board} = \sum_{k = 1}^{n} (n - k + 1)^{2} \ldotp \nonumber \]
Una vez que estemos seguros de que el patrón continúa, podemos usarlo para resolver el problema. ¡Así que adelante!
- ¿Cuántas casillas hay en un tablero de ajedrez de 10 × 10?
- ¿Qué cálculo harías para resolver ese problema para un tablero de ajedrez de 100 × 100?
Hay un patrón numérico que describe la cantidad de piezas que obtienes del problema “Puntos en un círculo”. Si quieres resolver el problema, ¡ve a por ello! Piensa en todas tus estrategias de resolución de problemas. Pero asegúrate de que cuando encuentres un patrón, puedas explicar por qué es el patrón adecuado para este problema, y no solo otro patrón que parece funcionar pero que podría no continuar.

