1.3: Estrategias de resolución de problemas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Piensa en el primer problema de este capítulo, el Problema ABC. ¿Qué hiciste para resolverlo? Incluso si no lo entendiste completamente por ti mismo, probablemente trabajaste hacia una solución y descubriste algunas cosas que no funcionaron.
A diferencia de los ejercicios, nunca hay una receta sencilla para resolver un problema. Puedes mejorar y mejorar en la resolución de problemas, tanto construyendo tus conocimientos previos como simplemente practicando. A medida que resuelves más problemas (y aprendes cómo los resolvieron otras personas), aprendes estrategias y técnicas que pueden ser útiles. Pero ninguna estrategia funciona cada vez.
George Pólya fue un gran campeón en el campo de la enseñanza de habilidades efectivas de resolución de problemas. Nació en Hungría en 1887, recibió su doctorado en la Universidad de Budapest, y fue profesor en la Universidad de Stanford (entre otras universidades). Escribió muchos trabajos matemáticos junto con tres libros, el más famoso, “Cómo resolverlo”. Pólya murió a los 98 años en 1985. [1]

George Pólya, alrededor de 1973
- Imagen de Pólya de Thane Plambeck de Palo Alto, California (Flickr) [CC BY 2.0 (http://creativecommons.org/licenses/by/2.0)], vía Wikimedia Commons
En 1945, Pólya publicó el libro corto Cómo resolverlo, que daba un método de cuatro pasos para resolver problemas matemáticos:
- Primero, hay que entender el problema.
- Después de entender, luego hacer un plan.
- Llevar a cabo el plan.
- Mira hacia atrás en tu trabajo. ¿Cómo podría ser mejor?
Todo esto está bien, pero ¿cómo haces realmente estos pasos?!?! ¡Los pasos 1. y 2. son particularmente misteriosos! ¿Cómo se “hace un plan”? Ahí es donde necesitas algunas herramientas en tu caja de herramientas, y algo de experiencia para aprovechar.
Mucho se ha escrito desde 1945 para explicar estos pasos con más detalle, pero lo cierto es que son más arte que ciencia. Aquí es donde las matemáticas se convierten en un esfuerzo creativo (y donde se vuelve tan divertido). Articularemos algunas estrategias útiles para la resolución de problemas, pero ninguna lista de este tipo estará completa. Esto es realmente solo un comienzo para ayudarte en tu camino. La mejor manera de convertirse en un experto solucionador de problemas es aprender bien el material de fondo, ¡y luego resolver muchos problemas!
Ya hemos visto una estrategia de resolución de problemas, a la que llamamos “Wishful Thinking”. ¡No tengas miedo de cambiar el problema! Hágase preguntas de “qué pasaría si”:
- ¿Y si la imagen fuera diferente?
- ¿Y si los números fueran más simples?
- ¿Y si solo inventé algunos números?
Debes estar seguro de volver al problema original al final, pero las ideas de ilusión pueden ser una estrategia poderosa para comenzar.
Esto nos lleva a la estrategia de resolución de problemas más importante de todas:
Estrategia de Resolución de Problemas 2 (¡Prueba Algo!).
Si realmente estás tratando de resolver un problema, el punto es que no sabes qué hacer justo al salir de la puerta de salida. ¡Solo necesitas probar algo! Pon lápiz en papel (¡o lápiz a pantalla o tiza a tablero o lo que sea!) y probar algo. Esto suele ser un paso importante para entender el problema; simplemente jugar un poco con él para entender la situación y averiguar qué está pasando.
E igualmente importante: Si lo que probaste primero no funciona, ¡prueba otra cosa! Juega con el problema hasta que tengas una idea de lo que está pasando.
La semana pasada, Alex pidió prestado dinero a varios de sus amigos. Finalmente le pagaron en el trabajo, por lo que llevó efectivo a la escuela para pagar sus deudas. Primero vio a Brianna, y le dio 1/4 del dinero que había traído a la escuela. Entonces Alex vio a Chris y le dio 1/3 de lo que le quedaba después de pagarle a Brianna. Por último, Alex vio a David y le dio 1/2 de lo que le quedaba. ¿Quién obtuvo más dinero de Alex?
Después de haber trabajado en el problema por su cuenta por un tiempo, hable a través de sus ideas con un compañero (aunque no lo haya resuelto). ¿Qué probaste? ¿Qué averiguaste sobre el problema? Este problema se presta a dos estrategias particulares. ¿Probaste alguno de estos mientras trabajabas en el problema? Si no, lee sobre la estrategia y luego pruébala antes de ver la solución.
Estrategia de Resolución de Problemas 3 (Dibuja una Imagen).
Algunos problemas son obviamente sobre una situación geométrica, y está claro que quieres dibujar un cuadro y marcar toda la información dada antes de intentar resolverla. Pero incluso para un problema que no es geométrico, como este, ¡pensar visualmente puede ayudar! ¿Se puede representar algo en la situación por una imagen?
Dibuja un cuadrado para representar todo el dinero de Alex. Entonces sombra 1/4 de la plaza —eso es lo que regaló a Brianna. ¿Cómo puede la imagen ayudarte a terminar el problema?
Después de haber trabajado tú mismo en el problema usando esta estrategia (o si estás completamente atascado), puedes ver la solución de otra persona.
Estrategia de Resolución de Problemas 4 (Make Up Numbers).
Parte de lo que dificulta este problema es que se trata de dinero, pero no hay números dados. Eso significa que los números no deben ser importantes. ¡Así que solo hazlos!
Puedes trabajar hacia adelante: Supongamos que Alex tenía alguna cantidad específica de dinero cuando se presentó en la escuela, digamos 100 dólares. Entonces averigua cuánto le da a cada persona. O puedes trabajar al revés: supongamos que le queda alguna cantidad específica al final, como $10. Desde que le dio a Chris la mitad de lo que le quedaba, eso significa que tenía 20 dólares antes de encontrarse con Chris. Ahora, trabaja hacia atrás y averigua cuánto obtuvo cada persona.
Mira la solución solo después de probar esta estrategia por ti mismo.
Si utilizas la estrategia de “Make Up Numbers”, ¡es muy importante recordar cuál era el problema original que te preguntaba! No quieres responder algo como “Todos obtuvieron $10”. Eso no es cierto en el problema original; ese es un artefacto de los números que inventaste. Entonces, después de que resuelvas todo, ¡asegúrate de volver a leer el problema y responder lo que se te pidió!
¿Cuántas casillas, de cualquier tamaño posible, hay en un tablero de ajedrez de 8 × 8? (La respuesta no es 64... ¡Es mucho más grande!)
Recuerda que el primer paso de Pólya es entender el problema. Si no estás seguro de lo que se te pide, o por qué la respuesta no es solo 64, ¡asegúrate de preguntarle a alguien!
Después de haber trabajado en el problema por su cuenta por un tiempo, hable a través de sus ideas con un compañero (aunque no lo haya resuelto). ¿Qué probaste? ¿Qué averiguaste del problema, aunque no lo hayas resuelto por completo?
Está claro que quieres dibujar un cuadro para este problema, pero incluso con el cuadro puede ser difícil saber si has encontrado la respuesta correcta. Los números se hacen grandes, y puede ser difícil hacer un seguimiento de su trabajo. Tu objetivo al final es ser absolutamente positivo de que encontraste la respuesta correcta. Nunca se le debe preguntar al maestro: “¿Es esto correcto?” En cambio, debes declarar: “¡Aquí está mi respuesta, y aquí está la razón por la que sé que es correcta!”
Estrategia de Resolución de Problemas 5 (Prueba un Problema Más Simple).
Pólya sugirió esta estrategia: “Si no puedes resolver un problema, entonces hay un problema más fácil que puedes resolver: encuéntralo”. También dijo: “Si no se puede resolver el problema propuesto, trate de resolver primero algún problema relacionado. ¿Te imaginas un problema relacionado más accesible?” En este caso, un tablero de ajedrez de 8 × 8 es bastante grande. ¿Se puede resolver el problema para tableros más pequeños? Como 1 × 1? 2 × 2? 3 × 3?
Por supuesto que el objetivo final es resolver el problema original. Pero trabajar con tableros más pequeños podría darte una idea y ayudarte a diseñar tu plan (ese es el paso de Pólya (2)).
Estrategia de Resolución de Problemas 6 (Trabajar sistemáticamente).
Si estás trabajando en problemas más simples, es útil hacer un seguimiento de lo que has descubierto y qué cambia a medida que el problema se complica más.
Por ejemplo, en este problema podrías hacer un seguimiento de cuántos cuadrados de 1 × 1 hay en cada tabla, cuántos cuadrados de 2 × 2 hay en cada tablero, cuántos cuadrados de 3 × 3 hay en cada tablero, y así sucesivamente. Podría realizar un seguimiento de la información en una tabla:
| tamaño del tablero | # de 1 × 1 cuadrados | # de 2 × 2 cuadrados | # de 3 × 3 cuadrados | # de 4 × 4 cuadrados | ... |
| 1 por 1 | 1 | 0 | 0 | 0 | |
| 2 por 2 | 4 | 1 | 0 | 0 | |
| 3 por 3 | 9 | 4 | 1 | 0 | |
| ... |
Estrategia de Resolución de Problemas 7 (Usa Manipulantes para Ayudarte a Investigar).
A veces incluso dibujar una imagen puede no ser suficiente para ayudarte a investigar un problema. ¡Tener materiales reales por los que te mueves a veces puede ayudar mucho!
Por ejemplo, en este problema puede ser difícil hacer un seguimiento de qué cuadrados ya has contado. Es posible que desee cortar 1 × 1 cuadrados, 2 × 2 cuadrados, 3 × 3 cuadrados, y así sucesivamente. De hecho, puedes mover los cuadrados más pequeños a través del tablero de ajedrez de manera sistemática, asegurándote de contar todo una vez y no contar nada dos veces.
Estrategia de Resolución de Problemas 8 (Buscar y Explicar Patrones).
A veces los números en un problema son tan grandes, de ninguna manera vas a contar todo a mano. Por ejemplo, si el problema en esta sección fuera alrededor de un tablero de ajedrez de 100 × 100, ¡no querrías pasar por contar todas las casillas a mano! Sería mucho más atractivo encontrar un patrón en las tablas más pequeñas y luego extender ese patrón para resolver el problema para un tablero de ajedrez de 100 × 100 solo con un cálculo.
Si aún no lo has hecho, extiende la mesa por encima de todo el camino a un tablero de ajedrez de 8 × 8, rellenando todas las filas y columnas. Usa tu mesa para encontrar el número total de cuadrados en un tablero de ajedrez de 8 × 8. Entonces:
- Describe todos los patrones que ves en la tabla.
- ¿Puedes explicar y justificar alguno de los patrones que ves? ¿Cómo puedes estar seguro de que continuarán?
- ¿Qué cálculo harías para encontrar el número total de cuadrados en un tablero de ajedrez de 100 × 100?
(Pronto volveremos a esta pregunta. Entonces, si en este momento no estás seguro de cómo explicar y justificar los patrones que encontraste, eso está bien).
Este reloj se ha roto en tres piezas. Si agrega los números en cada pieza, las sumas son números consecutivos. (Los números consecutivos son números enteros que aparecen uno tras otro, como 1, 2, 3, 4 o 13, 14, 15.)
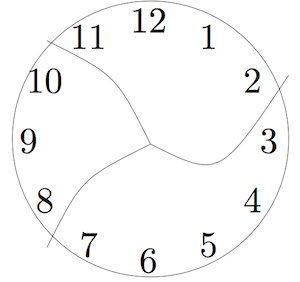
¿Se puede romper otro reloj en un número diferente de piezas para que las sumas sean números consecutivos? Supongamos que cada pieza tiene al menos dos números y que ningún número está dañado (por ejemplo, 12 no se divide en dos dígitos 1 y 2).
Recuerda que tu primer paso es entender el problema. Averiguar lo que está pasando aquí. ¿Cuáles son las sumas de los números en cada pieza? ¿Son consecutivos?
Después de haber trabajado en el problema por su cuenta por un tiempo, hable a través de sus ideas con un compañero (aunque no lo haya resuelto). ¿Qué probaste? ¿Qué avances has logrado?
Estrategia de resolución de problemas 9 (Encuentra las matemáticas, elimina el contexto).
A veces el problema tiene muchos detalles en él que no son importantes, o al menos poco importantes para comenzar. El objetivo es encontrar el problema matemático subyacente, luego volver a la pregunta original y ver si puedes resolverlo usando las matemáticas.
En este caso, preocuparse por el reloj y exactamente cómo se rompen las piezas es menos importante que preocuparse por encontrar números consecutivos que sumen al total correcto. Pregúntate a ti mismo:
- ¿Cuál es la suma de todos los números en la cara del reloj?
- ¿Puedo encontrar dos números consecutivos que den la suma correcta? ¿O cuatro números consecutivos? ¿O alguna otra cantidad?
- ¿Cómo sé cuándo terminé? ¿Cuándo debo dejar de buscar?
Por supuesto, resolver la pregunta sobre números consecutivos no es lo mismo que resolver el problema original. Tienes que volver atrás y ver si el reloj realmente puede romperse para que cada pieza te dé uno de esos números consecutivos. Tal vez puedas resolver el problema matemático, pero no se traduce en resolver el problema del reloj.
Estrategia de Resolución de Problemas 10 (Verifique sus Supuestos).
Al resolver problemas, es fácil limitar tu pensamiento agregando suposiciones adicionales que no están en el problema. Asegúrate de preguntarte: ¿Estoy limitando demasiado mi pensamiento?
En el problema del reloj, debido a que la primera solución tiene el reloj roto radialmente (las tres piezas se encuentran en el centro, por lo que parece rebanar un pastel), mucha gente asume que así es como debe romperse el reloj. Pero el problema no requiere que el reloj se rompa radialmente. Podría romperse en pedazos como este:
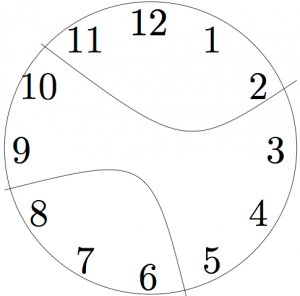
¿Asumiendo que el reloj se rompería de una manera específica? Intenta resolver el problema ahora, si aún no lo has hecho.




