1.5: Banco de problemas

Última actualización
Guardar como PDF

Page ID: 112790

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Tienes varias estrategias de resolución de problemas con las que trabajar. Aquí están los que hemos descrito hasta ahora (y probablemente se te ocurrieron aún más estrategias propias mientras trabajabas en problemas).

Pensamiento de deseos.
¡Prueba algo!
Dibuja un Cuadro.
Números de maquillaje.
Prueba un problema más simple.
Trabajar de manera sistemática.
Usa Manipulantes para Ayudarte a Investigar.
Busque y explique patrones.
Encuentra las matemáticas, elimina el contexto.
Verifique sus suposiciones.
Utilice una Variable.

Pruebe algunos de estos problemas, teniendo en cuenta estas estrategias. Si estás atascado en un problema, vuelve a esta lista y pregúntate cuál de las estrategias podría ayudarte a progresar.

Problema 6

Tienes ocho monedas y una balanza. Las monedas se parecen, pero una de ellas es una falsificación. La moneda falsificada es más ligera que las demás. Solo puedes usar la balanza dos veces. ¿Cómo puedes encontrar la moneda falsificada?

$index-19_1-300x275.png$

Problema 7

Tienes cinco monedas, no hay dos de las cuales pesan igual. En siete pesajes en una balanza, ¿puedes poner las monedas en orden de las más ligeras a las más pesadas? Es decir, ¿se puede determinar qué moneda es la más ligera, la siguiente más liviana,., la más pesada.

Problema 8

Tienes diez bolsas de monedas. Nueve de las bolsas contienen buenas monedas que pesan una onza cada una. Una bolsa contiene monedas falsificadas que pesan 1.1 onzas cada una. Tienes una báscula regular (digital), no una balanza. La escala es correcta a una décima de onza. En un pesaje, ¿se puede determinar qué bolsa contiene las monedas malas?

Problema 9

Supongamos que tiene una balanza. Tienes tres pesos diferentes, y puedes pesar cada número entero de 1 gramo a 13 gramos usando solo esos tres pesos. ¿Cuáles son los tres pesos?

Problema 10

Hay un montón de monedas en una mesa frente a ti. Tu amigo te dice cuántas de las monedas son heads-up. Tienes los ojos vendados y no puedes ver nada, pero puedes mover las monedas alrededor, y puedes voltearlas. Sin embargo, no se puede decir con solo sentirlas si las monedas están mostrando la cabeza o la cola. Tu trabajo: separar las monedas en dos pilas para que se muestre el mismo número de cabezas en cada pila.

Problema 11

La raíz digital de un número es el número obtenido sumando repetidamente los dígitos del número. Si la respuesta no es un número de un dígito, agregue esos dígitos. Continuar hasta que se alcance una suma de un dígito. Este dígito es la raíz digital del número.

Por ejemplo, la raíz digital de 98 es 8, ya que 9 + 8 = 17 y 1 + 7 = 8.

Registra las raíces digitales de los primeros 30 enteros y encuentra tantos patrones como puedas. ¿Puedes explicar alguno de los patrones?

Problema 12

Si se continuara esta celosía, ¿qué número estaría directamente a la derecha del 98? ¿Cómo puedes estar seguro de que tienes razón?

	3		6		9		12		...
1	2	4	5	7	8	10	11	13	...

Problema 13

Organice los dígitos del 0 al 9 para que el primer dígito sea divisible por 1, los dos primeros dígitos sean divisibles por 2, los tres primeros dígitos sean divisibles por 3, y continuando hasta que tenga los primeros 9 dígitos divisibles por 9 y el número entero de 10 dígitos divisible por 10.

Problema 14

Hay 25 alumnos y un maestro en clase. Después de un examen, todos chocan los cinco a todos los demás para celebrar lo bien que les fue. ¿Cuántos choca- cinco había?

Problema 15

Al limpiar tu viejo escritorio, encuentras un montón de sellos de 3¢ y 7¢. ¿Se puede hacer exactamente 11¢ de franqueo? ¿Se puede hacer exactamente 19¢ de franqueo? ¿Cuál es la mayor cantidad de franqueo que no puedes hacer?

Problema 16

Encuentra el número de ocho dígitos más grande compuesto por los dígitos 1, 1, 2, 2, 3, 3, 4 y 4 de tal manera que los 1 están separados por un dígito, los 2 están separados por dos dígitos, los 3 por tres dígitos, y los 4 por cuatro dígitos.

Problema 17

Kami tiene diez bolsillos y billetes de 44 dólares. Ella quiere tener una cantidad diferente de dinero en cada bolsillo. ¿Ella lo puede hacer?

Problema 18

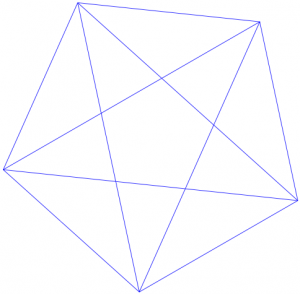
¿Cuántos triángulos de todos los tamaños y formas posibles hay en esta imagen?

$index-21_1-300x294.png$

Problema 19

Organice los dígitos 1—6 en un “triángulo de diferencia” donde cada número en la fila de abajo es la diferencia de los dos números por encima de él.

Ejemplo: A continuación se muestra un triángulo de diferencia, pero no funciona porque usa 1 dos veces y no tiene un 6:

4		5		3
	1		2
		1

Problema 20

Ciertas tuberías se venden en longitudes de 6 pulgadas, 8 pulgadas y 10 pulgadas. ¿Cuántas longitudes diferentes se pueden formar uniendo tres secciones de tubería?

Problema 21

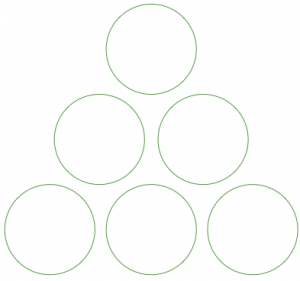
Coloca los dígitos 1, 2, 3, 4, 5, 6 en los círculos para que la suma de cada lado del triángulo sea 12. Cada círculo obtiene un dígito, y cada dígito se usa exactamente una vez.

$index-21_2-300x281.png$

Problema 22

Encuentra una manera de cortar una pizza circular en 11 trozos usando solo cuatro cortes rectos