5.7: Banco de problemas

Última actualización
Guardar como PDF

Page ID: 112633

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los problemas 34-36 te piden resolver problemas sobre un extraño veterinario que creó tres máquinas desmitificadoras.

Máquina Cat: Coloca un gato en el contenedor de entrada de esta máquina, presiona el botón y salta dos perros y un ratón.

Máquina para perros: Esta máquina convierte a un perro en un gato y un ratón.

Máquina de Ratón: Esta máquina puede convertir un ratón en un gato y tres perros.

Cada máquina también puede operar en reversa. Por ejemplo, si tienes dos perros y un ratón, puedes usar la primera máquina para convertirlos en un gato.

Problema 34

El veterinario te entrega dos gatos, y te pide que los conviertas en exactamente tres perros (sin perros extra y ningún otro animal). ¿Puedes hacerlo? En caso afirmativo, di qué proceso usarías. Si no, di por qué no.

Problema 35

El veterinario te entrega un perro. Dice que solo quiere gatos, pero no le importa cuántos. ¿Lo puedes ayudar? ¿Cómo?

Problema 36

El veterinario te entrega un gato. Dice que solo quiere perros, pero no le importa cuántos. ¿Lo puedes ayudar? ¿Cómo?

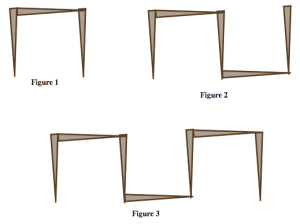
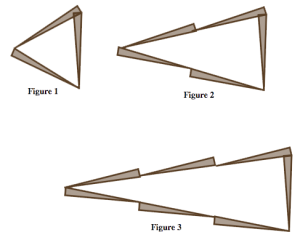
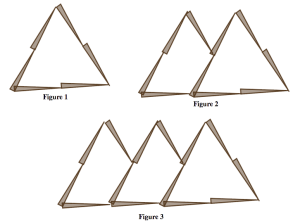
Los problemas 37-40 presentan varios patrones de crecimiento realizados con palillos de dientes. Para cada problema en el que trabajes, haz lo siguiente:

Describe en palabras e imágenes cómo ves crecer el patrón.
Calcula el número de palillos que necesitarías para construir la décima figura en el patrón. Justifica tu respuesta en base a cómo crece el patrón.
Calcula el número de palillos que necesitarías para construir la cifra número 100 en el patrón.
Describe cómo puedes averiguar el número de palillos de dientes en cualquier figura del patrón. Asegúrate de justificar tu respuesta en función de cómo crece el patrón.
¿Podrías hacer una de las figuras del patrón usando exactamente 25 mondadientes? En caso afirmativo, ¿cuál cifra? Si no, ¿por qué no? Justifica tu respuesta.
¿Podrías hacer una de las figuras del patrón usando exactamente 100 palillos de dientes? En caso afirmativo, ¿cuál cifra? Si no, ¿por qué no? Justifica tu respuesta.

Problema 37

$toothpicks1-300x224.png$

Problema 38

$toothpicks2-300x240.png$

Problema 39

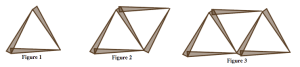
$toothpicks3-300x67.png$

Problema 40

$toothpicks4-300x223.png$

En un móvil, los brazos deben estar perfectamente equilibrados para que cuelgue correctamente. El artista Alexander Calder fue famoso por sus móviles artísticos.Aquí puedes ver algunos de sus increíbles trabajos. Haga clic en “Explorar obras”.

Los problemas 41-42 te presentan acertijos móviles. En estos acertijos:

Los objetos que tienen la misma forma tienen el mismo peso. (Entonces todos los círculos pesan igual, todos los cuadrados pesan lo mismo, etc.)
Supongamos que las cuerdas y varillas que sujetan los objetos juntos no tienen en cuenta el peso total.
Cada brazo del móvil debe tener exactamente el mismo peso.

Problema 41

En este rompecabezas:

El peso total es de 36 gramos.
Todas las formas pesan menos de 10 gramos.
Todos los pesos son números enteros.
Un círculo pesa más de un cuadrado.

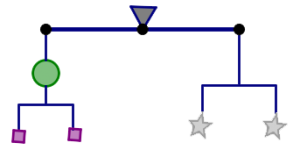
$mobile1-1-300x157.png$

Encuentra el peso de cada pieza. ¿Hay más de una respuesta? ¿Cómo sabes que tienes razón?

Problema 42

En este rompecabezas, el peso total es de 54 gramos.

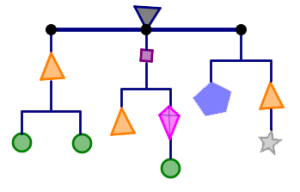
$mobile2-1-300x192.png$

Encuentra el peso de cada pieza. ¿Hay más de una respuesta? ¿Cómo sabes que tienes razón?