5.6: Álgebra estructural y procesal
- Page ID
- 112634
Cuando la mayoría de la gente piensa en álgebra desde la escuela, piensa en “resolver para x”. Se imaginan muchas ecuaciones con distintos niveles de complejidad, pero el objetivo es siempre el mismo: encontrar la cantidad desconocida. Esta es una visión procedimental del álgebra.
Incluso los estudiantes de primaria pueden estar expuestos a ideas en álgebra procesal. Esto sucede cada vez que piensan en cantidades desconocidas y tratan de resolverlas. Por ejemplo, cuando los estudiantes de primer grado aprenden a sumar y restar números “dentro de 10'”, frecuentemente deben abordar problemas como estos:
- \(3 + \_\_\_ = 7 \ldotp\)
- Encuentra varios pares de números que suman 10.
Aunque el álgebra procesal es importante, no es la habilidad más importante, y ciertamente no es toda la historia.
También necesitas fomentar el pensamiento sobre álgebra estructural en tus alumnos: usar símbolos para expresar significado en una situación. Si hay una x en tu página, deberías poder responder, “¿qué significa la x? ¿Qué representa?”
La mayor parte de lo que has hecho hasta ahora en este capítulo es álgebra estructural. Has usado letras y símbolos no para representar una sola cantidad desconocida, sino una cantidad variable. Por ejemplo, en la Sección 4 usaste letras para representar el “número de figura” o el “número de caso” en un patrón creciente. Las letras podían tomar diferentes valores, y las expresiones te daban información: cuántos mosaicos o palillos de dientes o estrellas necesitabas para construir esa figura en particular en ese patrón en particular.
- Considera la expresión\(a + 3\). Dar una situación del mundo real que pudiera ser representada por esta expresión. Comparte tu respuesta con tu pareja. Juntos, ¿se pueden llegar a tener aún más ideas?
- Supongamos que la expresión\(3c + 2\) representa el número de mosaicos utilizados en cualquier etapa de un patrón de crecimiento.
-
- Evaluar la expresión en\(c = 1, 2,\; \text{and}\; 3\). ¿Qué te dicen los valores sobre el patrón?
- ¿Se puede describir con palabras cómo está creciendo el patrón?
- ¿Se puede diseñar un patrón con azulejos que crezca de acuerdo a esta regla?
- ¿Dónde ves el “3” en tu patrón? ¿Dónde ves el “2” '? ¿Dónde ves el “
”?
Krystal estaba mirando este patrón, que puede resultarle familiar desde el Banco de Problemas:
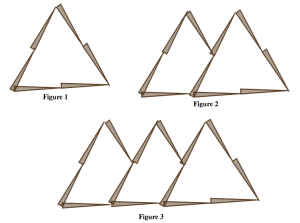
Ella anotó la ecuación
\[y = 4x + 2 \ldotp \nonumber \]
En la ecuación de Krystal, ¿qué
representa? ¿Qué
representa? ¿Cómo lo sabes?
Candice estaba pensando en este problema:
Hoy es el cumpleaños de Jennifer, y tiene el doble de edad que su hermano. ¿Cuándo volverá a tener el doble de edad que él?
Ella anotó la ecuación\(2n = m\). En la ecuación de Candice, ¿qué
representa? ¿Qué
representa? ¿Cómo lo sabes?
Sarah y David recogen monedas viejas. Supongamos que la variable
representa el número de monedas que Sarah tiene en su colección, y
representa el número de monedas que David tiene en su colección. ¿Qué diría cada una de estas ecuaciones sobre sus colecciones de monedas?
\[(a)\; k= \ell + 1 \qquad (b)\; k = \ell \qquad (c)\; 3k = 2 \ell \qquad (d)\; k = \ell - 11 \nonumber \]
Las imágenes de abajo muestran balanzas que contienen bolsas y bloques. Las bolsas están marcadas con un “?” ' porque contienen algún número desconocido de bloques. En cada imagen:
- Cada bolsa contiene el mismo número de bloques.
- La escala es equilibrada.
Para cada imagen, determine cuántos bloques hay en cada bolsa. Justifica tus respuestas.
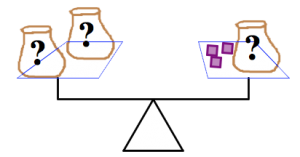
(a)
b)
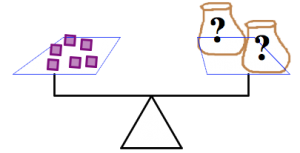
c)
Cuando estaba trabajando en el Problema 24, Kyle anotó estas tres ecuaciones.
(i)\[2m = 6 \ldotp \nonumber \]
ii)\[2x = x + 3 \ldotp \nonumber \]
iii)\[z + 5 = 2z + 3 \ldotp \nonumber \]
Haga coincidir cada ecuación con una imagen y justifique sus elecciones. Entonces resuelve las ecuaciones, y di (en una oración) lo que representa la solución.
Dibuja un rompecabezas de equilibrio que represente la ecuación
\[2h + 3 = h + 8 \ldotp \nonumber \]
Ahora resuelve el rompecabezas de equilibrio. ¿Dónde está el “
” en tu rompecabezas? ¿Qué representa?
Dibuja un rompecabezas de equilibrio que represente la ecuación
\[3b + 7 = 3b + 2 \ldotp \nonumber \]
Ahora resuelve la ecuación. Explique lo que sucede.
¿Cuál ecuación a continuación se parece más a la del Problema 27 anterior? Justifica tu elección.
- $$5+3=8\ ldotp$$
- $$\ frac {2} {3} +\ frac {1} {2} =\ frac {3} {5}\ ldotp$$
- $$5+3 = y\ ldotp$$
- $$\ frac {a} {5} =\ frac {5} {a}\ ldotp$$
- $$n + 3 = m\ ldotp$$
- $$3x = 2x+ x\ ldotp$$
- $$5k = 5k + 1\ ldotp$$
Dibuja un rompecabezas de equilibrio que represente la ecuación
\[4 \ell + 7 = 4 \ell + 7 \ldotp \nonumber \]
Ahora resuelve la ecuación. Explique lo que sucede.
¿Cuál ecuación a continuación se parece más a la del Problema 29 anterior? Justifica tu elección.
- $$5+3 = 8\ ldotp$$
- $$\ frac {2} {3} +\ frac {1} {2} =\ frac {3} {5}\ ldotp$$
- $$5+3 = y\ ldotp$$
- $$\ frac {a} {5} =\ frac {5} {a}\ ldotp$$
- $$n + 3 = m\ ldotp$$
- $$3x = 2x + x\ ldotp$$
- $$5k = 5k + 1\ ldotp$$
Crea un rompecabezas de equilibrio donde la solución no sea un número entero de bloques. ¿Puedes resolverlo? Explica tu respuesta.
Hay tres montones de rocas: la pila A, la pila B y la pila C. La pila B tiene dos rocas más que la pila A. La pila C tiene cuatro veces más rocas que la pila A. El número total de rocas en las tres pilas es 14.
- Usa x para representar el número de rocas en la pila A y escribe ecuaciones que describan las reglas anteriores. Después encuentra el número de rocas en cada pila.
- Usa x para representar el número de rocas en el pilote B y escribe ecuaciones que describan las reglas anteriores. Después encuentra el número de rocas en cada pila.
- Usa x para representar el número de rocas en el pilote C y escribe ecuaciones que describan las reglas anteriores. Después encuentra el número de rocas en cada pila.
Mira hacia atrás en Problemas 21—32. ¿Cuál de ellos se sintió como pensamiento algebraico estructural? ¿Cuál se sintió como el pensamiento algebraico procesal? ¿Alguno de los problemas se sintió como si involucrara ambos tipos de pensamiento?
Variables y Ecuaciones
Has visto que en álgebra, las letras y los símbolos pueden tener diferentes significados dependiendo del contexto.
- Un símbolo podría representar alguna cantidad desconocida.
- Un símbolo podría representar alguna cantidad que varía. (De ahí el término “variable” para describir estos símbolos.)
De la misma manera, las ecuaciones pueden representar cosas diferentes.
- Pueden representar un problema a resolver. Este es el tipo de cuestión de álgebra procesal tradicional.
- Pueden representar una relación entre dos o más cantidades. Por ejemplo,\(A = s^{2}\) representa la relación entre el área de un cuadrado y su longitud lateral.
- Pueden representar identidades: verdades matemáticas. Por ejemplo, $$x^ {2} - 1 = (x + 1) (x - 1) $$$siempre es cierto, por cada valor de. No hay nada que resolver, y ninguna relación entre cantidades variables. (Si intentas “resolver por”, obtendrás la ecuación\(0 = 0\), al igual que viste en el Problema 29. ¡No muy satisfactorio!)
Dar un ejemplo de cada tipo de ecuación. Asegúrese de decir lo que representan los símbolos en las ecuaciones.
Responde las siguientes preguntas sobre la ecuación
\[x^{2} - 1 = (x + 1)(x - 1) \ldotp \nonumber \]
- Evaluar ambos lados de la ecuación anterior para\(x = 1, 2, 3, 4,\; \text{and}\; 5\). ¿Qué pasa?
- Utilice la propiedad distributiva de multiplicación sobre suma para expandir el lado derecho de la ecuación y simplificarla.
- Usa la ecuación para calcular\(99^{2}\) rápidamente, sin usar una calculadora. Explica cómo lo hiciste.