6.1: Revisión del Modelo de Puntos y Cajas

Última actualización
Guardar como PDF

Page ID: 112798

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comencemos con una revisión rápida del valor positorial, diferentes bases y nuestro modelo “Dots & Boxes” para pensar en estas ideas.

La regla 1aria2

Siempre que hay dos puntos en una sola caja, “explotan”, desaparecen y se convierten en un punto en la caja a la izquierda.

Ejemplo: Nueve puntos 110×2 en el sistema

Comenzamos colocando nueve puntos en el cuadro más a la derecha.

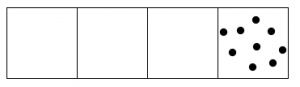
$Explode1a-300x87.png$

Dos puntos en esa caja explotan y se convierten en un punto en la caja a la izquierda.

$Explode1b-300x83.png$

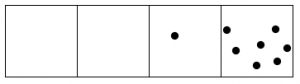
$Explode1c-300x84.png$

Una vez más, dos puntos en esa caja explotan y se convierten en un punto en la caja a la izquierda.

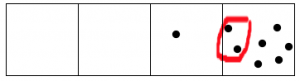
$Explode1d-300x81.png$

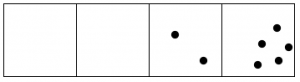
$Explode1e-300x82.png$

¡Lo volvemos a hacer!

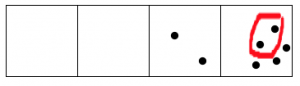
$Explode1f-300x86.png$

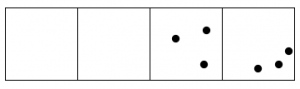
$Explode1g-300x89.png$

Oye, ahora tenemos más de dos puntos en la segunda caja, ¡así que esos pueden explotar y moverse!

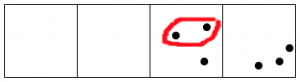
$Explode1h-300x82.png$

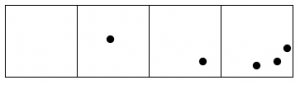
$Explode1i-300x85.png$

Y la caja más a la derecha todavía tiene más de dos puntos.

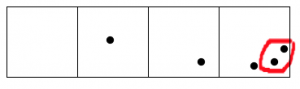
$Explode1j-300x89.png$

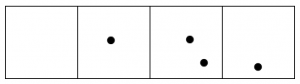
$Explode1k-300x84.png$

Sigue adelante, hasta que ninguna caja tenga dos puntos.

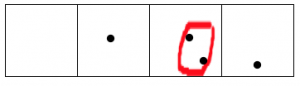
$Explode1l-300x86.png$

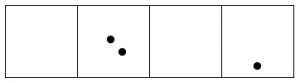
$Explode1m-300x83.png$

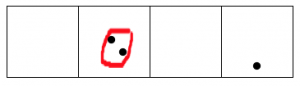
$Explode1n-300x86.png$

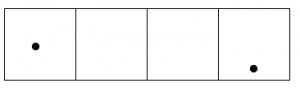
$Explode1o-300x88.png$

Después de todo esto, leyendo de izquierda a derecha nos quedamos con un punto, seguido de cero puntos, cero puntos y un punto final.

Contestar: El código 210×1 para nueve puntos es: 1001.

La regla 1aria.3

Siempre que hay tres puntos en una sola caja, “explotan”, desaparecen y se convierten en un punto en la caja a la izquierda.

Ejemplo: Quince puntos en el sistema 1"3

Esto es lo que sucede con quince puntos:

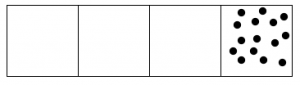
$Explode3a-300x85.png$

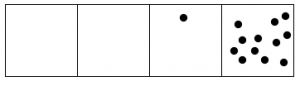
$Explode3b-300x86.png$

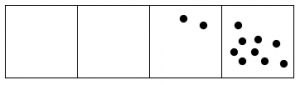
$Explode3c-300x85.png$

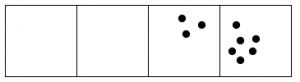
$Explode3d-300x82.png$

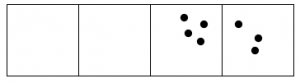
$Explode3e-300x83.png$

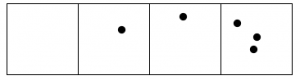
$Explode3f-300x80.png$

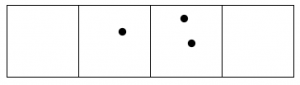
$Explode3g-300x85.png$

Contestar: El código 110×3 para quince puntos es: 120.

Definición

Recordemos que los números escritos en el sistema 1← 2 se denominan números binarios o base dos.

Los números escritos en el sistema 1"3 se denominan números base tres.

Los números escritos en el sistema 1"4 se denominan números base cuatro.

Los números escritos en el sistema 1"10 se denominan números base diez.

En general, los números escritos en el sistema 1← b se denominan números base b.

En un sistema de números base b, cada lugar representa una potencia de b, lo que significa$b^{n}$ para algún número entero n. Recuerde que esto significa b multiplicado por sí mismo n veces:

El lugar más a la derecha es el lugar de las unidades o unas. (¿Por qué es esto un poder de b?)
El segundo lugar es el lugar “b”. (En la base diez, es el lugar de las decenas.)
El tercer lugar es el “$b^{2}$” lugar. (En la base diez, ese es el lugar de los cientos. Tenga en cuenta que$10^{2} = 100$.)
El cuarto lugar es el “$b^{3}$” lugar. (En la base diez, ese es el lugar de miles, ya que$10^{3} = 1000$.)
Y así sucesivamente.

notación

Siempre que estamos tratando con números escritos en diferentes bases, usamos un subíndice para indicar la base para que no pueda haber confusión. Entonces:

$102_{three}$es un número base tres (léelo como “uno-cero-dos base tres”). Este es el código base tres para el número once.
$222_{four}$es un número base cuatro (léelo como “dos-dos-dos base cuatro”). Este es el código base cuatro para el número cuarenta y dos.
$54321_{ten}$es un número base diez. (Está bien decir “cincuenta y cuatro mil trescientos veintiuno”. ¿Por qué?)

Si la base no está escrita, asumimos que es la base diez.

Recuerda: cuando veas el subíndice, estás viendo el código para algún número de puntos.

Pensar/Parejar/Compartir

Trabaje cuidadosamente los dos ejemplos anteriores para asegurarse de recordar y comprender cómo funciona el modelo “Dots & Boxes”. Entonces contesta estas preguntas:

Cuando escribimos 9 en base 2, ¿por qué escribimos$1001_{two}$ en lugar de solo$11_{two}$?

Cuando escribimos 15 en base 3, ¿por qué escribimos$120_{three}$ en lugar de solo$12_{three}$?

¿Cuántos dígitos diferentes necesitas en un sistema base 7? ¿En un sistema base 12? ¿En un sistema base b? ¿Cómo lo sabes?

Por su cuenta

Trabaja en los siguientes ejercicios por tu cuenta o con un compañero.

En la base 4, cuatro puntos en una caja valen un punto en el cuadro un lugar a la izquierda.
1. ¿Cuál es el valor de cada caja?
2. ¿Cómo se escribe$29_{ten}$ en base 4?
3. ¿Cómo se escribe$132_{four}$ en base 10?
En nuestro familiar sistema base diez, diez puntos en una caja valen un punto en la caja un lugar a la izquierda.
1. ¿Cuál es el valor de cada caja?
2. Cuando escribimos el número base diez 7842:
  - ¿Qué cantidad representa el “7”?
  - El “4” es de cuatro grupos de qué valor?
  - El “8” son ocho grupos de qué valor?
  - El “2” son dos grupos de qué valor?
Escribe los siguientes números de puntos en la base dos, la base tres, la base cinco y la base ocho. ¡Dibuja el modelo “Dots & Boxes” si te ayuda a recordar cómo hacer esto! (Nota: todos estos números están escritos en base diez. Cuando no decimos lo contrario, se debe asumir la base diez.) $$ (a)\; 2\ qquad (b)\; 17\ qquad (c)\; 27\ qquad (d)\; 63\ ldotp$$
Convierte estos números a nuestro sistema base diez más familiar. Dibuja puntos y cajas y “desexplota” los puntos si te ayuda a recordar. $$ (a)\; 1101_ {dos}\ qquad (b)\; 102_ {tres}\ qquad (c)\; 24_ {cinco}\ qquad (d)\; 24_ {nueve}\ ldotp$$

Pensar/Parejar/Compartir

Calcula rápidamente cada uno de los siguientes. Escribe tu respuesta en la misma base que el problema.

$131_{ten}$veces diez.

$263207_{eight}$veces ocho.

$563872_{nine}$veces nueve.

Utilice el sistema 1← 10 para explicar por qué multiplicar un número entero en la base diez por diez da como resultado simplemente agregar un cero al extremo derecho del número.

Supongamos que tiene un número entero escrito en base b. ¿Cuál es el efecto de multiplicar ese número por b? Justifica lo que dices.