6: Razonamiento con Datos
- Page ID
- 107778
Este capítulo resume algunos de los conceptos y relaciones clave de las estadísticas de una sola variable que podríamos encontrar útiles para caracterizar las mediciones, particularmente cuando hemos medido una cantidad en varias ocasiones, o hemos medido muchos miembros individuales de una población o colección. Esto no pretende ser una introducción exhaustiva a la estadística, y no sustituye en modo alguno a un curso de estadística adecuado. Sin embargo, señala algunas conexiones que podemos hacer entre la medición y caracterización de datos y la descripción científica de la naturaleza que a veces buscamos.
6.1 Medición y Muestreo
En las ciencias naturales a menudo necesitamos estimar o medir una cantidad o conjunto de cantidades que sea demasiado grande, demasiado numerosas o demasiado complejas para caracterizarlas completamente de una manera eficiente. Podemos caracterizarla aproximadamente con una muestra representativa. Una muestra representativa es un pequeño subconjunto del conjunto que se mide para caracterizar el todo.
Considera un ejemplo. En pequeños arroyos de cabecera, muchos aspectos de la salud biótica están vinculados con el tamaño del sustrato: la arena, guijarros o cantos rodados que componen el lecho del arroyo. Pero no es práctico medir todos los gajillions de partículas dispersas por todo el lecho. En cambio, intentamos obtener una muestra más pequeña pero representativa
del material del lecho. Esto se puede hacer de varias maneras diferentes, pero dos métodos comunes son: 1) tomar uno o más cubos llenos de sedimento del lecho de la corriente y hacer un análisis detallado del tamaño de partícula en un laboratorio; y 2) medir el tamaño de 100 partículas seleccionadas aleatoriamente del lecho. Ambos métodos obtienen una muestra, pero cada uno puede representar el verdadero cauce de una manera diferente. El método del bucket requiere que escojamos sitios de muestreo en el lecho de la corriente. Nuestras opciones podrían estar sesgadas hacia aquellos lugares donde el muestreo podría ser más fácil, el lecho más visible o el agua menos profunda. En este caso, nuestros resultados podrían no ser representativos del arroyo en su conjunto.
Figura 6.1: Adoquines en el lecho del río Cub, Idaho.
El método del “conteo de guijarros”, por otro lado, está destinado a producir una muestra más aleatoria de la. Una persona vadeando en el arroyo pisa diagonalmente por el canal, y en cada paso coloca su índice de la puntera de su bota. Se mide el diámetro de la partícula que su dedo toca primero, y luego repite el proceso, - a través del canal hasta que haya medido 100 (o algún número predeterminado mayor) partículas. En principio, esta muestra aleatoria es más representativa de la, particularmente a medida que aumenta el número de partículas en la muestra. Por supuesto, al aumentar el número de partículas en la muestra se incrementa el tiempo y esfuerzo utilizado, pero con rendimientos decrecientes para mejorar la precisión de la muestra.
\(^{1}\)A este método se le llama a veces el método del “recuento de guijarros de Wolman” para los Rojos Wolman, el científico que primero lo describió y popularizó.
Hablando hipotéticamente, un método alternativo de conteo de guijarros podría ser estirar una cinta métrica a través de la corriente y medir el tamaño de partícula a intervalos regulares, digamos cada medio metro. Podemos llamar a esta estrategia el método del “conteo de puntos”. Esta alternativa es atractiva ya que asegura que las muestras se distribuyan uniformemente a través del canal y que las muestras no se agrupen en el espacio. Sin embargo, es concebible que dicho muestreo sistémico pueda conducir a un sesgo sistemático\(^{2}\).
\(^{2}\)El muestreo sistemático es a veces un enfoque más sencillo y sencillo para el muestreo. Sin embargo, si el entorno dentro del cual se realiza el muestreo pudiera tener alguna estructura sistemática, el muestreo sistemático podría sesgar inadvertidamente la muestra.
Si por ejemplo el tuviera racimos o patrones de partículas en él que tuvieran una longitud de onda de 0.5 m, podría estar muestreando inadvertidamente solo una cierta parte de la parte superior de cada duna, lo que podría sesgar sus resultados hacia tamaños de partículas que se concentran en las crestas de dunas. Por lo tanto, una muestra aleatoria suele ser preferible ya que es menos susceptible a este tipo de sesgo sistemático.
Las cantidades derivadas de una muestra aleatoria no están relacionadas entre sí de la misma manera que el tamaño de un grano medido durante un recuento de guijarros no influye en el tamaño del siguiente. Parte de nuestra secuencia de datos podría verse así:
12, 2, 5, 26, 4, 28, 19, 29, 3, 15, 31, 19, 24, 27, 7, 22, 28, 33, 21, 28, 13, 15, 25, 10, 14, 13, 16, 18, 33, 5
La naturaleza aleatoria de este conjunto de datos nos permite utilizar algunas de las formas familiares de describir nuestros datos, al tiempo que aumenta nuestra confianza de que también estamos caracterizando adecuadamente el sistema más grande que estamos muestreando.
6.1.1 Ejemplo: marca-recaptura
Una preocupación frecuente del ecologista de vida silvestre es la abundancia y salud de una especie particular de interés. Idealmente, podríamos contar y evaluar la salud de cada individuo en una población, pero eso generalmente no es práctico, ¡diablos, nos cuesta contar y evaluar la salud de todos los humanos en un pueblo pequeño! Sin embargo, en lugar de tratar de localizar a cada individuo, podemos hacer un trabajo decente simplemente tomando una muestra aleatoria de la población y realizando el análisis deseado en esa muestra aleatoria. Como hemos visto, si somos lo suficientemente cuidadosos para evitar sesgos en nuestro muestreo, podemos estar razonablemente seguros de que nuestra muestra nos dirá algo útil (y no engañoso) sobre la mayor población de la que proviene la muestra.
Si nuestra preocupación es principalmente con la población de una especie objetivo en un área determinada, podemos usar un método llamado marca-recaptura, o captura-recaptura. La premisa básica es simple: capturamos algún número de individuos en una población a la vez, los pegamos, etiquetamos o marcamos de tal manera que posteriormente puedan ser reconocidos como individuos que fueron capturados previamente, luego los liberamos. Tiempo después, después de que estos individuos se hayan dispersado en la población en su conjunto, capturamos otro conjunto. La proporción de los individuos en la segunda captura que están marcados debería, en teoría, ser la misma que la proporción de toda la población que marcamos para empezar. Si el número de individuos que marcamos la primera vez es N\(_{1}\), el número que capturamos la segunda vez es N\(_{2}\), y el número en el segundo grupo que llevó marcas de la primera captura es M, se puede estimar la población P más simplemente como:
P =\(\frac{N_{1} N_{2}}{M}\) (6.1)
Esto viene de la suposición de que nuestra muestra cada vez es aleatoria, y que los individuos marcados tienen exactamente la misma probabilidad de estar en la segunda captura que en la primera: 1/ P. Por lo tanto, si muestreamos y marcamos una fracción N\(_{1}\)/P la primera vez y la muestra N 2 la segunda vez, entonces debemos esperar que se marque una fracción M/N\(_{2}\) de ellos.
Por supuesto, todo este plan se puede frustrar si no se cumplen algunos supuestos clave. Por ejemplo, necesitamos que la población esté “cerrada” —es decir, los individuos no ingresan y salen de la población de tal manera que nuestra muestra no viene del mismo conjunto de individuos cada vez. También podrían surgir problemas si nuestra muestra “aleatoria” no es aleatoria, si de alguna manera el proceso de marcar a los individuos los perjudica o hace que su probabilidad de re-captura sea más o menos probable, o si el tiempo que les permitimos para volver a mezclarse con su población no era apropiado. En el último punto, se puede imaginar que si recapturamos tortugas 10 minutos después de liberarlas de su primera captura, nuestra segunda muestra no será muy aleatoria. Por otro lado, si recuperamos peces marcados 20 años después de que se marcaron por primera vez, muchos de ellos pueden haber muerto y ser reemplazados por sus crías, y así se viola nuestra asunción de una población “cerrada”. Por lo que en la planificación de un estudio de marca-recaptura, es necesario tomar en cuenta el espacio y las escalas de tiempo.
Vale la pena señalar que el método aquí descrito es sobre la versión más despojada de marca-recaptura. Existen muchas modificaciones en el método y la ecuación utilizada para calcular la población que da cuenta de la inmigración/emigración, múltiples recapturas, algunas posibles re-recapturas, etc. También hay métodos relacionados con el etiquetado y marcado que pueden ser utilizados para explorar la dispersión de individuos, rutas migratorias y mucho más!
6.2 Describir medidas
Las mediciones, o “datos”, pueden informar e influir en gran parte de los objetivos de trabajo de un gerente de refuente, ya que transmiten información sobre los sistemas de interés. A veces los datos hablan por sí mismos: los números brutos son lo suficientemente claros y convincentes como para que no se necesite hacer nada más para que hablen los datos. Más comúnmente, sin embargo, los datos necesitan ser resumidos y caracterizados a través de uno o más procesos de procesamiento de datos y reducción de datos. El procesamiento podría referirse simplemente a un conjunto rutinario de algoritmos aplicados a los datos sin procesar para que satisfagan los objetivos del proyecto o problema. La reducción de datos generalmente resume un gran conjunto de datos con un conjunto más pequeño de estadísticas descriptivas. Para un conjunto de medidas de una cantidad simple, por ejemplo, podríamos desear saber:
Cosas que a menudo queremos saber sobre nuestros datos
1. ¿qué es una observación típica?
2. ¿Qué tan diversos son los datos?
3. ¿Cómo deben caracterizarse estas propiedades de los datos para diferentes tipos de cantidades?
El primer punto sugiere el uso de nuestras medidas de tendencia central: media, mediana y modo. El segundo objetivo se refiere a las medidas de propagación o dispersión en los datos. Por ejemplo, ¿qué tan cerca están la mayoría de los valores en el conjunto de datos de la media?
6.3 Tendencia central
La tendencia central de un conjunto de datos es un valor central característico que puede ser la media, mediana o modo. Cuál de estas medidas de tendencia central caracteriza mejor el conjunto de datos depende de la naturaleza de los datos y de lo que deseamos caracterizar al respecto. La mayoría de nosotros ya estamos familiarizados con el concepto de una media, o valor av- erage de un conjunto de números. Normalmente solo sumamos todos los valores observados y dividimos por el número de valores para obtener la media. En realidad, esta es la media aritmética, y hay muchas formas alter- nativas de computar diferentes tipos de medios que son útiles en circunstancias particulares, pero no nos preocuparemos por estos ahora. Para nuestros propósitos, la media aritmética es la media a la que nos referimos cuando decimos media o promedio. Sería decir lo contrario. Antes de continuar, discutamos brevemente los diferentes tipos de notas que podríamos usar al hablar de datos. Para definir algo como la media con una ecuación, nos gustaría hacer que la definición sea lo más general posible, es decir, aplicable a todos los casos y no a uno solo. Entonces necesitamos una notación que, por ejemplo, no especifique el número de puntos de datos en el conjunto de datos sino que permita que eso varíe. Si queremos encontrar la media (llámala x ï) de un conjunto de 6 puntos de datos (x 1, x 2, y así sucesivamente), una fórmula correcta podría verse así:
\(\bar{x}=\frac{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}}{6}\)(6.2)
y por supuesto esto es correcto. Pero no podemos usar la misma fórmula para un conjunto de datos que tenga 7 u 8 valores, o cualquier otra cosa que no sea 6 valores. Fur- thermore, no es muy conveniente tener que escribir cada término en el numerador si el conjunto de datos es realmente grande. Entonces necesitamos una taquigrafía que sea a la vez breve y no específica de un cierto número de puntos de datos. Un enfoque es escribir:
\(\bar{x}\)=\(\frac{x_{1}+x_{2}+...+x_{n}}{n}\) (6.3)
donde entendemos que n es el número de observaciones en el conjunto de datos. Los puntos suspensivos en el numerador denota todos los valores faltantes entre x\(_{2}\) y x\(_{n}\), el último valor a incluir en el promedio. El uso de este tipo de ecuaciones para definir la media es mucho más general que el primer ejemplo, y es más compacto siempre y cuando haya 4 o más valores a promediar.
Una forma adicional de ver la media definida es usar la llamada “notación sigma”\(^{3}\), donde se ve así:
\(\bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i}\)(6.4)
\(^{3}\)Este símbolo es una práctica taquigrafía para el proceso de agregar un montón de cantidades, pero también sirve para asustar a muchos estudiantes pobres. Una vez que te das cuenta de que es solo una abreviatura para enumerar todos los términos a agregar (x 1 + x 2 +...) y algunas de las reglas para hacerlo, se vuelve un poco menos temible.
donde la gran σ es el símbolo de suma. Si nunca antes te has encontrado con esto, aquí te explicamos cómo interpretarlo: el “summand”, el material después de la σ, debe interpretarse como una lista de valores (en este caso x\(_{i}\)) que necesitan sumarse, e i comienza en 1 y aumenta hasta llegar a n. Se pueden ver las reglas de lo que quiero decir mirando el texto de abajo y por encima de la σ. Abajo donde dice i = 1 eso significa que i comienza con un valor de 1 y aumenta con cada término agregado hasta i = n, que es el último término. Entonces al final, se puede interpretar esto para que tenga un significado idéntico a las expresiones equivalentes anteriores, pero en algunos casos esta notación puede ser más compacta y explícita. También se ve más elegante y más intimidante, por lo que la gente a veces usará esta notación para asustarte, a pesar de que te da el mismo resultado que la segunda ecuación anterior.
6.3.1 Media versus Mediana
Cuadro 6.1: Un día digno de captura en el lago.
Para algunos conjuntos de datos, la media puede ser una forma engañosa de describir la tendencia central. Si tu fileta después de un día de pesca incluye 5 tipos de pez de media libra, un lucioperca de 3/4 libras, 4 uno de 16 libras, sería correcto pero engañoso decir que el tamaño promedio del pez que capturaste era de 2.1 libras. La distribución de pesos incluye un valor atípico distante, el, que distorsiona en gran medida la media, pero todos los demás peces que capturaste pesaban una libra o menos. Podríamos decir en este caso que la media es sensible a los valores atípicos.
La mediana es una medida alternativa de tendencia central que no es sensible a los valores atípicos. Es simplemente el valor para el cual la mitad de las ob- raciones son mayores y la mitad son menores. De su captura de pesca, el lucioperca de 0.75 libras representa el valor medio, ya que 5 peces (los crappies) eran más pequeños y 5 peces (los pequeños y el almizcle) eran más grandes. La mediana también se puede considerar como el valor medio en
una lista ordenada de valores, aunque realmente solo hay un valor medio distinto cuando se tiene un número impar de observaciones. En el caso de que tengas un número par de observaciones, la mediana está a medio camino entre las dos observaciones medias.
6.3.2 Modo
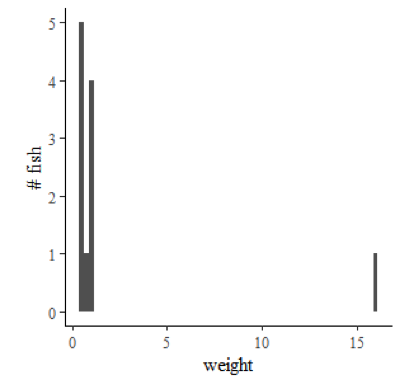
Figura 6.2: Histograma que muestra la frecuencia de observaciones de pesos de peces. La altura de cada barra corresponde al número de peces en cada uno de los contenedores de peso a lo largo del eje horizontal. Los valores son arrugados a los bordes debido a la gran dispersión de datos. En algunos casos, los datos multimodales pueden ser sugerentes de una muestra mixta; es decir, hay más de un solo tipo de cosa o de más de una sola fuente en la muestra.
El modo es el valor o rango de valores que ocurre con mayor frecuencia en un conjunto de datos. Dado que capturó 5 peces de media libra y menos de cualquier otro valor de peso en el conjunto de datos, el modo de esta distribución es de 0.5 libras. Ahora bien, si los pesos que hemos reportado anteriormente son realmente redondeados de pesos medidos verdaderos que difieren ligeramente, esta definición se vuelve menos satisfactoria. Por ejemplo, supongamos que los tipos de pez de media libra pesaban en realidad 0.46, 0.49, 0.5, 0.55 y 0.61 libras. Ninguno de estos tiene en realidad el mismo valor, entonces ¿podemos decir que esto sigue siendo un modo? De hecho podemos si elegimos toor bin estos datos. Podríamos decir que nuestros pesos de pescado caen en contenedores que van de 0.375 a 0.625, 0.625 a 0.875, 0.875 a 1.125, y así sucesivamente. En este caso, dado que todos nuestros tipos de pez caen en el rango de 0.375 a 0.625 (que es de 5 ± 1/8 lbs), este rango de tamaño sigue siendo el modo del conjunto de datos. Esto lo podemos ver visualmente en un histograma, que es solo un gráfico de barras que muestra la frecuencia con la que las mediciones caen dentro de cada bin en un rango (Figura 6.2).
6.4 Spread
Como se mencionó anteriormente, una forma de cuantificar la dispersión de un conjunto de datos es encontrar la diferencia entre cualquier observación dada y el valor esperado o media muestral. Si escribimos esto:
x\(_{i}\) -\(\bar{x}\), (6.5)
podemos llamar a cada una de esas diferencias un residual. A podría usarse para desmarcar la relación entre los puntos de datos individuales y la media de la muestra, pero no caracteriza por sí mismo la dispersión de todo el conjunto de datos. Pero, ¿y si sumamos todos estos residuos y dividimos por el número de puntos de datos? Bueno, esto solo debería darnos cero, ¡según la definición de la media! Pero supongamos en cambio que cuadramos los residuos antes de sumarlos. La fórmula se vería así:
\(\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\)(6.6)
Esta expresión se define como la varianza y se denota extrañamente con σ 2, pero verás por qué en un minuto. Al cuadrar los residuos, la mayoría de ellos fueron más grandes y los negativos fueron positivos. También acentuó aquellos puntos de datos atípicos que estaban más alejados de la media. Ahora bien, si tomamos la raíz cuadrada de la varianza, nos quedamos con un valor positivo finito que muy bien representa cuán lejos suelen estar los datos de la media: la desviación estándar de la muestra, o σ\(^{4}\). La definición formal de desviación estándar se ve así:
\(\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\)(6.7)
El nos da un buen sentido de qué tan lejos de la media se encuentra una medición típica. Ahora podemos caracterizar una muestra como que tiene un valor medio de\(\bar{x}\) y desviación estándar de σ, o diciendo que los valores típicos son\(\bar{x}\) ± σ. Pero en realidad, si calculamos\(\bar{x}\) y σ, los límites establecidos por\(\bar{x}\) − σ y\(\bar{x}\) + σ solo contienen alrededor del 68% de los puntos de datos. Si queremos incluir más de los datos, podríamos usar dos desviaciones estándar por encima y por debajo de la media, en cuyo caso hemos delimitado más del 95% de los datos.
6.5 Error e incertidumbre
Una pieza de información que hasta ahora hemos omitido de nuestra lista de propiedades que definen completamente el valor de una cantidad es la incertidumbre. Esto es particularmente importante cuando estamos cuantificando algo que se ha medido directamente o derivado de mediciones. Así, para definir aún más completamente el valor de una cantidad medida, debemos incluir alguna estimación de la incertidumbre asociada con el número que se le asigna. Esto a menudo se verá así:
x = x\(_{best}\) ± δ x, (6.8)
donde x es lo que estamos tratando de cuantificar, x\(_{best}\) es nuestra mejor suposición de su valor, y δ x es nuestra estimación de la incertidumbre. Aunque dependerá de la cantidad en cuestión, nuestra mejor estimación a menudo será el resultado de una sola medición o, mejor aún, la media de varias mediciones repetidas.
El valor preferido x\(_{best}\) para una cantidad de interés a menudo será la media de mediciones repetidas de esa cantidad.
6.5.1 Incertidumbre en las cantidades medidas
Todas las mediciones están sujetas a cierto grado de incertidumbre, derivada de la resolución limitada del instrumento o escala utilizada para realizar la medición, o de errores aleatorios o sistemáticos resultantes del método o circunstancias de medición. Consideremos un ejemplo:
Supongamos que dos biólogos pesqueros midieron cada uno las longitudes de diez de las truchas de arroyo capturadas durante la travesía de electropesca del Problema 3.7. Ambos utilizaron tablas con escalas idénticas impresas en ellas, graduadas a medio centímetro. Luego planean juntar sus mediciones para obtener un conjunto de datos de 20 peces. Uno de ellos fue entrenado para juntar las aletas de la cola para hacer esta medida, mientras que el otro no lo fue. Además, porque deseaban no
dañar a los peces, hicieron sus mediciones rápidamente, aunque el pez se tambaleara y se movió durante la medición. ¿Cuáles son las posibles fuentes de error y qué tan grandes son relativas entre sí?
Para empezar, implícito en las graduaciones de este tablero es que el usuario no puede leer con confianza nada mejor que medio centímetros fuera de la escala. Él o ella puede, sin embargo, interpolar visualmente entre dos graduaciones adyacentes para mejorar la precisión (ver más abajo). Sin embargo, este paso es inherentemente subjetivo y limita la certeza de la medición. Podríamos llamar a este error instrumental porque su magnitud la establece el instrumento o dispositivo que utiliza para realizar la medición. Una forma de reducir esta fuente de error es usar una escala más graduada.
El error instrumental se fija por la resolución del dispositivo utilizado para realizar una medición, y por lo general solo se puede reducir mediante el uso de un instrumento más preciso.
Una segunda fuente de error surge de las mediciones apresuradas y el hecho de que los peces no fueron necesariamente cooperativos. Quizás la boca a veces no estaba presionada todo el camino contra el alto, o el pez no estaba bien alineado con la escama. Algunas longitudes pueden haber sido demasiado grandes o pequeñas como resultado, produciendo una fuente de error que fue esencialmente aleatoria. En efecto, podemos llamar a este error aleatorio ya que su signo y magnitud no están en gran medida relacionados de una medición a la siguiente. Reducir esta fuente de error en este caso requeriría ya sea un esfuerzo más cuidadoso y deliberado para alinear e inmovilizar al pez, o realizar múltiples mediciones del mismo pez. Ambas soluciones podrían poner en peligro a los peces y, por lo tanto, pueden no ser deseables.
Los errores de medición aleatorios pueden mitigarse repitiendo mediciones.
Una tercera fuente de error se asocia con la diferencia en la forma en que los dos científicos trataron la aleta de cola. Las medidas de longitud hechas con las aletas pellizcadas juntas generalmente serán más largas que las que no las tienen. Si hubieran medido el mismo grupo de diez peces, un conjunto de mediciones habría arrojado longitudes consistentemente más pequeñas que las otras. Este es un error sistemático, y a menudo puede ser problemático y difícil de detectar. Esto resalta la necesidad de una declaración procesal que establezca pautas claras para las mediciones donde puedan surgir tales fuentes de error sistemático.
Los errores sistemáticos dan como resultado datos que se desvían sistemáticamente de los valores verdaderos. Estos errores a menudo pueden ser más difíciles de detectar y corregir, y los esfuerzos de recolección de datos deben hacer grandes esfuerzos para eliminar cualquier fuente de error sistemático.
Cada uno de estos tipos de error puede afectar los resultados de las mediciones, y deben ser cuantificados e incluidos en la descripción de la mejor estimación de la longitud de los peces. Pero los errores pueden afectar la mejor estimación de diferentes maneras. El error instrumental, como se describió anteriormente, puede ser en sí mismo aleatorio o sistemático. La escala impresa en una de las tablas de medición de peces podría estirarse por un factor de 3% en comparación con la otra, resultando en un error sistemático. De igual manera, una tabla podría estar hecha de plástico que es más resbaladizo que el otro y por lo tanto más difícil alinear los peces. Esto podría resultar en un error aleatorio adicional asociado con ese dispositivo. Pero, ¿cuáles son las relaciones entre este tipo de errores y la mejor estimación que estamos buscando?
¿
¿Error o variación? Preguntas para hacerte
1. ¿Cuáles fueron las posibles fuentes de error en sus mediciones? ¿Son aleatorias o sistemáticas?
2. ¿Cómo se puede distinguir entre el error en la medición y la variabilidad natural?
6.5.2 Variabilidad real
No todas las desviaciones de la media son errores. Para cantidades reales en la naturaleza, no hay una buena razón para suponer que, por ejemplo, todas las truchas de arroyo de 0 años serán de la misma longitud. De hecho, esperamos que haya variaciones reales entre peces de una sola cohorte de edad debido a diferencias en genética, patrones de alimentación y otros factores reales. Si estamos midiendo un grupo de peces de edad 0 para entender cómo esos peces varían en tamaño, entonces al menos parte de la variación en nuestros datos refleja la variación real en la longitud de esos peces. ¿Cómo nos burlamos de la variación que se debe a errores de la variación que se debe a la variabilidad real?
A menudo, un buen enfoque es tratar de estimar de forma independiente la magnitud de los errores de medición. Si esos errores de medición son aproximadamente de la misma magnitud que las variaciones (residuales) dentro de los datos, entonces puede que no sea posible identificar la variabilidad real. Sin embargo, en el caso más probable de que nuestras mediciones sean razonablemente ac- curadas y tengan pequeños errores de medición en comparación con su dispersión sobre la media, entonces las variaciones indicadas probablemente reflejen la variabilidad verdadera.
Esta observación nos devuelve a nuestra pregunta anterior: cuando buscamos caracterizar alguna cantidad, ¿cómo debemos identificar nuestra mejor estimación y nuestro grado de incertidumbre en esa estimación? Si queremos caracterizar una sola cantidad y nuestra certeza de que nuestra mejor estimación es cercana o igual al valor verdadero, debemos usar la media de las mediciones repobladas de este valor y el error estándar de esas mediciones. El error estándar se puede estimar fácilmente dividiendo la desviación estándar de las medidas repetidas por el número de mediciones n:
SE =\(\frac{σ}{\sqrt{n}}\) (6.9)
Esto debería ser equivalente a la desviación estándar de una serie de estimaciones de la media x ï, si se tomaron varias muestras de la población completa de mediciones. Al igual que la desviación estándar, podemos estar alrededor de 68% seguros de que el rango x mejor + SE a x mejor − SE incluye el valor verdadero que deseamos caracterizar, pero si usamos 1.96 SE en su lugar, podemos tener 95% de confianza\(^{5}\). Una declaración completa, entonces, de nuestra mejor estimación con 95% de certeza en este contexto es decir:
x = x\(_{best}\) ± 1.96 SE, (6.10)
Si en cambio deseamos una caracterización de un valor y rango típicos para algo que tenga variabilidad real entre individuos en una población, generalmente lo describiremos con la desviación media y estándar.
x = x mejor ± 1.96 σ, (6.11)
\(^{5}\)Tenga en cuenta que actualmente estamos asumiendo que nuestras mediciones están distribuidas noramalmente.
6.6 Distribuciones
El tipo de datos de los que hemos estado hablando hasta ahora es univariado: una sola cantidad con valores variables como el diámetro de una partícula de lecho de arroyo, o la longitud de un pez. Como sabemos, no todas las truchas de arroyo de 0 años son del mismo tamaño. En una captura de primer paso de 50 peces, por ejemplo, debemos esperar alguna variabilidad en la longitud que pueda reflejar la edad, la genética, la estructura social o cualquier otro factor que pueda influir en el desarrollo. La variación puede visualizarse gráficamente de varias maneras. Empezaremos con un histograma.
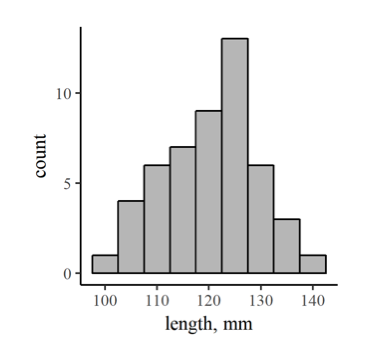
Figura 6.3: Histograma que muestra la distribución de mediciones simuladas (aleatorias) de la longitud de 100 serpientes.
Un histograma muestra la distribución de un conjunto de mediciones discretas —es decir, el rango de valores y el número de puntos de datos que caen en cada uno de un número de bins, que son solo rangos de valores (112.5 a 117.5 es un bin, 117.5 a 122.5 otro.). Esto se puede llamar distribución de frecuencias, y un histograma es una de las mejores formas de visualizar una distribución de frecuencias (Figura 6.3).
Pero, ¿y si tuviéramos datos distribuidos uniformemente? Una distribución uniforme significa que es igualmente probable que encontremos un individuo con una longitud en el extremo inferior (97.5-102.5 mm) del rango como cualquier otro. Eso se vería bastante diferente —no habría joroba en medio del histograma, sino más bien un número similar de medidas de cada longitud posible. La distribución uniforme es grande: de hecho, contamos con uniformidad a veces. Si estás en el casino y rodando los dados, probablemente asumas (a menos que seas deshonesto) que hay una probabilidad igual de que tirarás un 6 ya que hay que tirar un 1 en cualquier dado dado dado. Podemos llamarlo una distribución uniforme de probabilidad para un solo rollo de un dado. Pero ¿y si el juego que estás jugando cuenta la suma de los números en 5 dados? ¿Todavía hay una probabilidad uniforme de obtener algún valor total de 5 a 30?
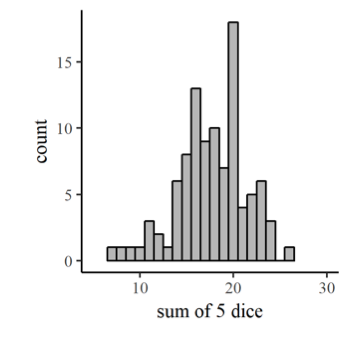
Figura 6.4: Suma de los valores de cinco dados, rodados 100 veces cada uno.
De hecho, podríamos simular eso con bastante facilidad eligiendo al azar (con un programa de computadora como R\(^{6}\) o Excel) cinco enteros entre 1 y 6 y sumarlos juntos. La Figura 6.4 muestra la gráfica que sale. Parece una curva de campana, ¿verdad? Bueno, ¿qué tan probable es que consigas cinco 1's o cinco 6's? No muy, ¿verdad? Tampoco es más probable que obtengas uno de 1,2,3,4 y 5 cada uno, ¿verdad? Sin embargo, hay múltiples formas de obtener un 1,2,3,4 y 5 con diferentes dados que muestran cada uno de los números posibles, mientras que solo hay una forma de obtener los seis y una forma de obtener todos los números. Así que hay mejores posibilidades de que obtengas un surtido aleatorio de números, algunos más altos y otros más bajos, y su suma tenderá hacia un valor central, la media de los valores posibles. Entonces, dado que su colección de rollos de los dados represente una muestra aleatoria de una distribución uniforme, la suma de varios rollos se distribuirá normalmente.
\(^{6}\)R es un software de primera elección para el análisis y modelado de datos de propósito general. Es software libre, funciona en la mayoría de las plataformas informáticas y tiene capacidades casi infinitas debido al repositorio de paquetes aportado por el usuario. Conoce más sobre R en https://cran.r-project.org/
¿Qué tiene que ver con los peces? Si tomamos muestras de trucha de arroyo aleatoriamente de un arroyo y medimos sus longitudes, podríamos esperar que se distribuyan normalmente. Describir tal distribución normal con cantidades como la media y la desviación estándar nos da el poder de comparar diferentes poblaciones, o de decidir si algunos individuos son valores atípicos. Las tuercas y tornillos de esas comparaciones dependen de cómo el tipo de distribución representada por la población. Una distribución normal ideal se define por esta ecuación:
\(f(x)=\frac{1}{\sqrt{2 \pi \sigma}} \exp \left[\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right]\)(6.12)
y su gráfica, en el contexto de nuestra hipotética distribución original de longitudes de peces, se parece a la línea roja de la Figura 6.5. Para comparar las distribuciones continuas y discretas, hemos dividido los recuentos en cada bin por el número total en la muestra (50), para producir una distribución de densidad. La línea azul es solo una interpolación suavizada de los centros superiores de cada barra en la distribución discreta, por lo que generalmente refleja la densidad de datos dentro de cada bin. Como puede ver, la densidad de distribución discreta y las funciones de distribución normal continua son similares, pero hay algunas protuberancias en la distribución discreta que no coinciden del todo con la curva continua. Sin embargo, como puedes imaginar, esa diferencia se volvería menos pronunciada a medida que tu conjunto de datos crezca. Relacionada con esto, entonces, está la idea de que su confianza en la tendencia central y propagación derivada de su conjunto de datos debería mejorar con más datos.
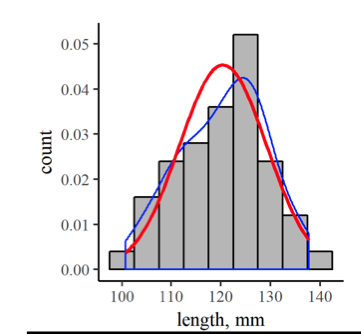
Figura 6.5: Densidad de distribución discreta superpuesta (barras), densidad continua interpolada a partir de la distribución discreta (línea azul) y una función de distribución continua ideal con la misma media y desviación estándar.
1. Descargue los datos del conjunto de datos InchLake2 de Derek Ogle del sitio web de datos FishR. Mediante una hoja de cálculo o un paquete de análisis de datos, aísle el bluegill del conjunto de datos e identifique lo siguiente:
(a) Longitud media de la aleta azul.
b) Desviación estándar de la longitud de la aleta azul.
(c) Peso medio de agalla azul.
d) Desviación estándar del peso de la aleta azul.
La gráfica y tabla de datos a continuación y derecha muestran mediciones de longitudes de trucha de arroyo del paso #1 de la campaña de electropesca descrita en Problema 3.7. Utilice estos recursos para responder a las siguientes preguntas:
(a) A juzgar por el histograma de la Figura 2, ¿el conjunto de datos contiene solo un modo o más de uno? ¿Cuál podría ser la razón de esto?
b) ¿Cuál es la media y la desviación estándar para la porción (presunta) de edad 0 de esta muestra?
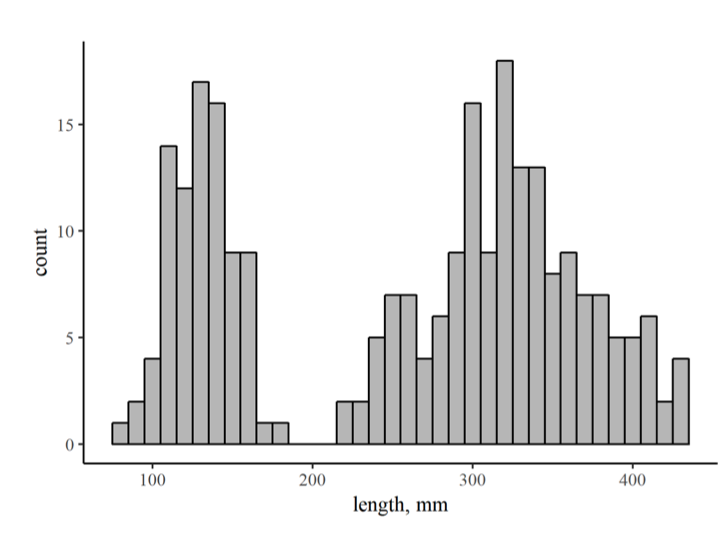
Figura 6.6: Distribución completa de frecuencias de longitudes de trucha de arroyo del paso de electropesca #1 del Problema 3.7.
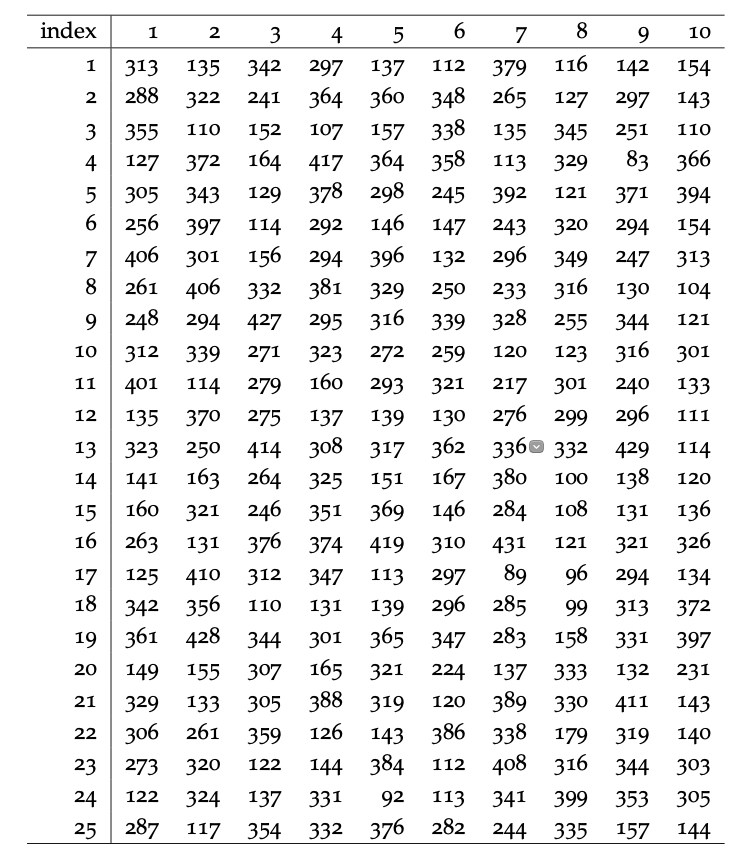
Cuadro 6.2: Datos de longitud de trucha de arroyo del paso de electropesca #1. Todas las longitudes en mm.