1.5: Más que la suma de sus partes
- Page ID
- 112183
Motivamos este primer capítulo al notar que si bien muchas estructuras del mundo real son compositivas, los resultados de observarlas a menudo no lo son. La razón es que la observación es inherentemente “con pérdida”: para extraer información de algo, hay que dejar caer los detalles. Por ejemplo, se almacena un número real redondeándolo con cierta precisión. Pero si los detalles son realmente relevantes en una operación dada del sistema, entonces el resultado observado de esa operación no será el esperado. Esto es claro en el caso del error de redondeo, pero también aparece en dominios no numéricos: observar un sistema complejo rara vez es suficiente para predecir su comportamiento porque la observación es con pérdida.
Un tema central en la teoría de categorías es el estudio de estructuras y mapas que preservan la estructura. Un mapa f: X → Y es una especie de observación del objeto X a través de una relación especificada que tiene con otro objeto, Y. Por ejemplo, pensar en X como el sujeto de un experimento e Y como un medidor conectado a X, lo que nos permite extraer ciertas características de X al observar la reacción de Y.
Preguntar qué aspectos de X uno quiere preservar bajo la observación f se convierte en la pregunta “¿en qué categoría estás trabajando?”. Como ejemplo, hay muchas funciones f de\(\mathbb{R}\) a\(\mathbb{R}\), y podemos pensarlas como observaciones: en lugar de ver x “directamente”, solo observamos f (x). De todas las funciones f:\(\mathbb{R}\) →\(\mathbb{R}\), solo algunas de ellas conservan el orden de los números, solo algunas de ellas conservan la distancia entre los números, solo algunas de ellas conservan la suma de números, etc. Vamos a registrarnos con un ejercicio; se puede encontrar una solución en el Capítulo 1.
Alguna terminología: una función f:\(\mathbb{R}\) →\(\mathbb{R}\) se dice que es
(a) conservación de orden si x ≤ y implica f (x) ≤ f (y), para todos x, y ∈ R; 1
(b) preservación métrica si |x - y| = | f (x) - f (y) |;
c) adicional-conservando si f (x + y) = f (x) + f (y).
Para cada una de las tres propiedades definidas anteriormente llamarlo foo encontrar una f que es foo preservando y un ejemplo de una f que no es foo preservando. ♦
En la teoría de categorías queremos mantener el control sobre qué aspectos de nuestros sistemas se están conservando bajo diversas observaciones. Como dijimos anteriormente, cuanto menos estructura se conserva por nuestra observación de un sistema, más “sorpresas” ocurren cuando observamos sus operaciones. Se podría llamar a estas sorpresas efectos generativos.
Al utilizar la teoría de categorías para explorar los efectos generativos, seguimos las ideas básicas del trabajo de Adam [Ada17]. Él profundiza mucho más en el tema de lo que podemos aquí; ver Sección 1.5. Pero como se mencionó anteriormente, también debemos usar este capítulo para dar un calentamiento teórico de orden para la teoría de categorías completa por venir.
primer vistazo a los efectos generativos
Para explorar la noción de efecto generativo necesitamos una especie de sistema, una especie de observación y una operación a nivel de sistema que no sea preservada por la observación. Empecemos con un ejemplo sencillo.
Un sistema sencillo. Considera tres puntos; los llamaremos •, ◦ y ∗. En este ejemplo, un sistema simplemente será una forma de conectar estos puntos entre sí. Podríamos pensar en nuestros puntos como sitios en una red eléctrica, con un sistema que describe la conexión por líneas eléctricas, o como personas susceptibles a alguna enfermedad, con un sistema que describe interacciones que pueden conducir al contagio. Como ejemplo abstracto de un sistema, existe un sistema donde • y ◦ están conectados, pero ninguno está conectado a ∗. Dibujaremos esto así:
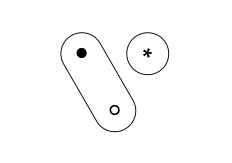
Las conexiones son simétricas, por lo que si a está conectada a b, entonces b está conectada a a. Las conexiones también son transitivas, lo que significa que si a está conectado a b, y b está conectado a c, entonces a está conectado a c; es decir, todos a, b y c están conectados. La amistad no es transitiva el amigo de mi amigo no es necesariamente mi amigo pero la posible comunicación de un concepto o una enfermedad sí lo es.
Aquí representamos dos sistemas más, uno en el que ninguno de los puntos está conectado, y otro en el que están conectados los tres puntos.

Hay cinco sistemas en total, y los representamos justo debajo.
Ahora que hemos definido el tipo de sistema que queremos discutir, supongamos que Alice está observando este sistema. Su observación de interés, que llamamos Φ, extrae una sola característica de un sistema, a saber si el punto • está conectado al punto ∗; esto es lo que quiere saber. Su observación del sistema será una asignación de verdadero o falso; ella asigna verdadero si • está conectado a ∗, y falso en caso contrario. Entonces Φ asigna el valor true a los dos sistemas siguientes:
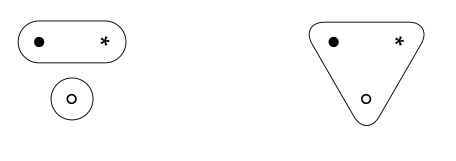
y Φ asigna el valor false a los tres sistemas restantes:

La última pieza de configuración es dar una especie de operación que Alice quiera realizar en los propios sistemas. Es una operación muy común que surgirá muchas veces a lo largo del libro llamado join. Si el lector ha estado siguiendo el arco de la historia, la expectativa aquí es que la observación de conectividad de Alice no sea compositiva con respecto a la operación de unión de sistemas; es decir, habrá efectos generativos. Veamos qué significa esto.
Uniéndose a nuestros sistemas simples. La unión de dos sistemas A y B se realiza simplemente combinando sus conexiones. Es decir, diremos la unión de los sistemas A y B, denotarlo A\(\lor\) B, tiene una conexión entre los puntos x e y si hay algunos puntos z 1,., z n tal que cada uno de los siguientes son ciertos en al menos uno de A o B: x está conectado a z 1, z i está conectado a z i +1, y z n está conectado a y. En un sistema de tres puntos, la definición anterior es exagerada, pero queremos decir algo que funcione para sistemas con cualquier número de elementos. La forma de alto nivel de decirlo es “tomar el cierre transitivo de la unión de las conexiones en A y B”. En nuestro sistema de tres elementos, significa por ejemplo que
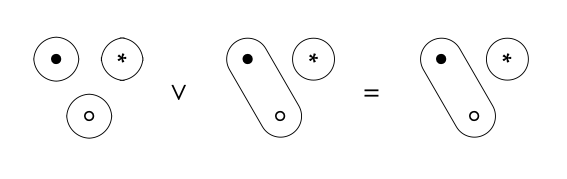
y

¿Cuál es el resultado de unirse a los dos sistemas siguientes?
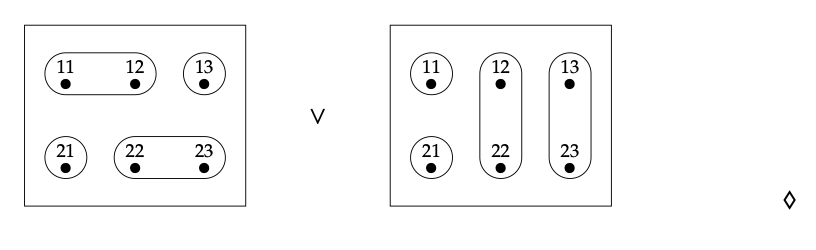
- Ya estamos listos para ver el efecto generativo. No queremos construirlo demasiado este ejemplo se ha hecho lo más simple posible pero veremos que la observación de Alice no logra preservar la operación join. Hemos estado denotando su observación midiendo si • y ∗ están conectados por el símbolo Φ; devuelve un resultado booleano, ya sea verdadero o falso.
Vemos arriba en la Ec. (1.2) que\(\Phi\left(\odot^{\circ}\right)=\Phi\left(^{\circ} \%\right)=\text { false }\): en ambos casos •noestá conectado a ∗. Por otro lado, cuando unimos estos dos sistemas como en la Ec. (1.3), vemos que\(\Phi\left(\Omega^{\circ} \vee^{\circ} \theta\right)=\Phi\left(^{\circ}\right)=\text { true: }\) en el sistema unido, • está conectado a ∗. La pregunta que le interesa a Alice, la de Φ, es inherentemente perdidora con respecto a unirse, y no hay forma de arreglarla sin una observación más detallada, una que incluya no sólo ∗ y • sino también ◦.
Si bien este fue un ejemplo sencillo, cabe señalar que si existe el potencial de tales efectos, es decir, determinar si una observación es conservadora de la operación, puede ser información increíblemente importante para conocer. Por ejemplo, Alice podría ser la encargada de armar las opiniones de dos autoridades locales sobre el posible contagio entre una persona infectada • y una persona vulnerable ∗. Alice ha notado que si extraen información por separado de sus datos brutos y combinan los resultados, da una respuesta diferente a la que combinaran sus datos brutos y extraen información de ellos.
Sistemas de pedidos
La teoría de categorías tiene que ver con la organización y las estructuras de capas. En esta sección explicaremos cómo se puede derivar el funcionamiento de los sistemas de unión a partir de una estructura más básica: el orden. Veremos que si bien la unión no se conserva por la observación de conectividad de Alice Φ, el orden sí.
Para comenzar, observamos que los propios sistemas están ordenados en una jerarquía. Dados los sistemas A y B, decimos que A ≤ B si, siempre que x esté conectado a y en A, entonces x está conectado a y en B. Por ejemplo,
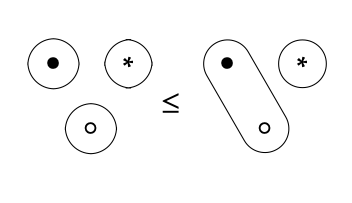
Esta noción de ≤ lleva al siguiente diagrama:
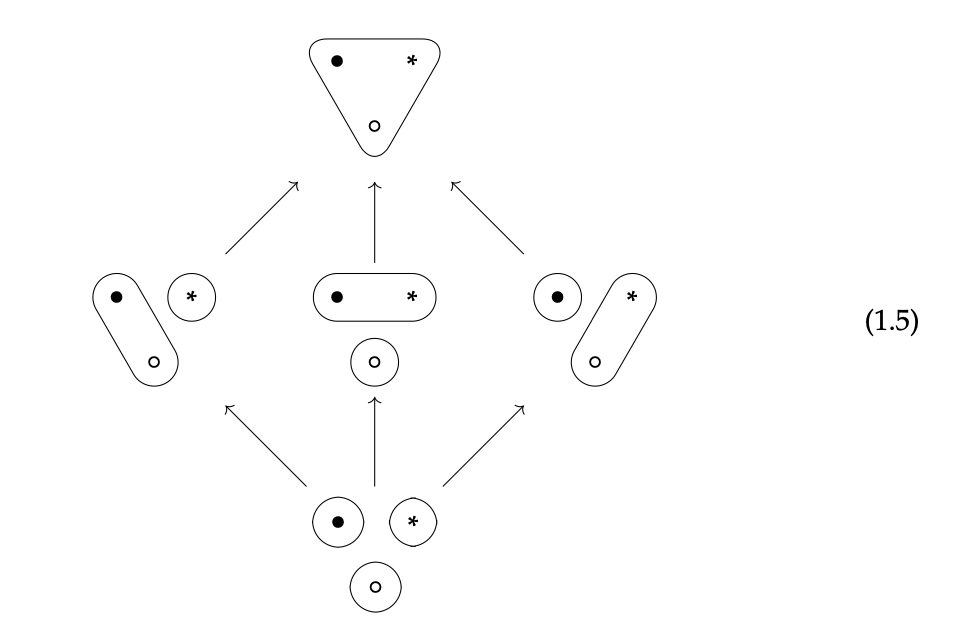
donde una flecha del sistema A al sistema B significa A ≤ B. Tales diagramas se conocen como diagramas de Hasse.
Como decíamos anteriormente, la noción de unión se deriva de este orden. De hecho, para cualquiera de los dos sistemas A y B en el diagrama de Hasse (1.5), el sistema unido A ‖ B es el sistema más pequeño que es más grande que tanto A como B. Es decir, A ≤ (A\(\lor\) B) y B ≤ (A\(\lor\) B), y para cualquier C, si A ≤ C y B ≤ C entonces (A\(\lor\) B) ≤ C. Pasemos por esto con un ejercicio.
- Anota todas las particiones de un conjunto de dos elementos {•, ∗}, ordenarlos como arriba y dibujar el diagrama de Hasse.
- Ahora haz lo mismo para un conjunto de cuatro elementos, digamos {1, 2, 3, 4}. Debe haber 15 particiones.
Elija dos sistemas cualesquiera en su diagrama Hasse de 15 elementos, llámalos A y B.
3. ¿Qué es A, a partir de la definición que se da en el párrafo anterior Ec. (1.3)?
4. ¿Es cierto que A ≤ (A\(\lor\) B) y B ≤ (A\(\lor\) B)?
5. ¿Cuáles son todos los sistemas C para los que tanto A ≤ C como B ≤ C.
6. ¿Es cierto que en cada caso, (A\(\lor\) B) ≤ C? ♦
El conjunto\(\mathbb{B}\) = {true, false} de booleanos también tiene un orden, false ≤ true:

Así false ≤ false, false ≤ true, y true ≤ true, pero true ≠ false. Es decir, A ≤ B si A implica B. \(^{2}\)
Para cualquier A, B en B, podemos volver a escribir A\(\lor\) B para significar el menor elemento que sea mayor que tanto A como B.
Usando el orden false ≤ true on\(\mathbb{B}\) = {true, false}, lo que es:
- verdadero\(\lor\) falso?
- falso\(\lor\) verdad?
- verdad\(\lor\) verdad?
- falso\(\lor\) falso? ♦
Volvamos a nuestros sistemas con •, ◦, y ∗, y la función “•” de Alice está conectada a la función ∗, a la que llamamos Φ. Toma cualquier sistema de este tipo y devuelve ya sea verdadero o falso. Tenga en cuenta que el mapa Φ conserva el orden ≤: si A ≤ B y hay una conexión entre • y∗ en A, entonces también hay tal conexión en B. La posibilidad de un efecto generativo se captura en la desigualdad
\(\Phi(A) \vee \Phi(B) \leq \Phi(A \vee B)\). (1.8)
Vimos en la página 4 que esto puede ser una desigualdad estricta: mostramos dos sistemas A y B con Φ (A) = Φ (B) = falso, entonces Φ (A) ‖ Φ (B) = falso, pero donde Φ (A\(\lor\) B) = verdadero. En este caso, existe un efecto generativo.
Estas ideas capturan las ideas más básicas en la teoría de categorías. Más directamente, hemos visto que el mapa Φ conserva alguna estructura pero no otras: conserva el orden pero no se une. De hecho, hemos visto aquí indicios de nociones más complejas de la teoría de categorías, sin hacerlas explícitas; estas incluyen las nociones de categoría, functor, colimit y adjunction. En este capítulo exploraremos estas ideas en el entorno elemental de conjuntos ordenados.


