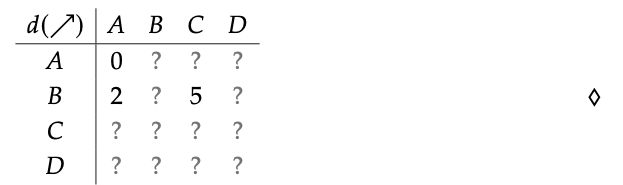2.3: Enriquecimiento

En esta sección presentaremos categorías V, donde V es un preorden monoidal simétrico. Veremos que las categorías de Bool son preordenes, y que las categorías de costos son una buena generalización de la noción de espacio métrico.

V -categorías

Si bien las categorías V pueden definirse incluso cuando V no es simétrica, es decir, solo obedece a las condiciones (a) — (c) de la Definición 2.2, ciertas cosas no funcionan del todo bien. Por ejemplo, veremos más adelante en el Ejercicio 2.75 que la condición de simetría es necesaria para que existan productos de categorías V. En fin, aquí está la definición.

Definición: 2.46.

Sea V = (V, ≤, I,) un preorden monoidal simétrico. A V -categoría X consta de dos componentes, satisfaciendo dos propiedades. Para especificar X,

i) se especifica un conjunto Ob (X), cuyos elementos se denominan objetos;

(ii) por cada dos objetos x, y, se especifica un elemento X (x, y)\(\in\) V, llamado hom-object. \(^{2}\)

Los constituyentes anteriores se requieren para satisfacer dos propiedades:

(a) para cada objeto x\(\in\) Ob (X) tenemos I ≤ X (x, x), y

(b) por cada tres objetos x, y, z\(\in\) Ob (X), tenemos X (x, y) X (y, z) ≤ X (x, z). Llamamos a V la base del enriquecimiento para X o decimos que X se enriquece en V.

Ejemplo 2.47.

Como veremos en la siguiente subsección, a partir de cada preorden podemos construir una categoría Bool, y viceversa. Entonces, para tener una idea de las categorías V, consideremos el preorden generado por el diagrama de Hasse:

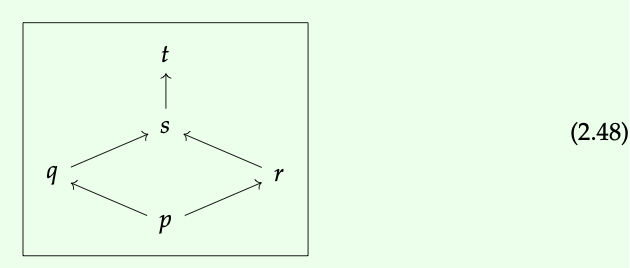
¿Cómo corresponde esto a un Bool -categoría X? Pues bien, los objetos de X son simplemente los elementos del preorden, es decir, Ob (X) = {p, q, r, s, t}. A continuación, para cada par de objetos (x, y) necesitamos un elemento de\(\mathbb{B}\) = {false, true}: simplemente tomar true si x ≤ y, y false si es contrario. Entonces, por ejemplo, ya que s ≤ t y t\(\nleq\) s, tenemos X (s, t) = verdadero y X (t, s) = falso. Recordando del Ejemplo 2.27 que la unidad monoidal I de Bool es cierta, es sencillo comprobar que esto obedece tanto a (a) como a (b), por lo que tenemos una categoría Bool-.

En general, a veces es conveniente representar una categoría V X con una matriz cuadrada. Las filas y columnas de la matriz corresponden a los objetos de X, y la entrada (x, y) th es simplemente el hom-object X (x, y). Entonces, por ejemplo, el preorden anterior en la Ec. (2.48) puede ser representado por la matriz

Prepedidos como Bool -categorías

Nuestro compañero Peter Gates ha llamado a la teoría de categorías “un rezumo primordial”, porque gran parte de ella se puede definir en términos de otras partes de la misma. No hay ningún lugar para llamar con razón el principio, porque ese comienzo puede definirse en términos de otra cosa. Que así sea; esto es parte de la diversión.

Teormo 2.49.

Existe una correspondencia uno a uno entre los pedidos anticipados y las categorías Bool-.

Aquí nos encontramos en el rezumado, porque estamos diciendo que los pedidos anticipados son los mismos que Bool -categorías, mientras que Bool es en sí mismo un preorder. “Entonces, ¿Bool es como... enriquecido en sí mismo?” Sí, cada preorden, incluido Bool, está enriquecido en Bool, como veremos ahora. Prueba de Teorema 2.49. Comprobemos que podemos construir una preorden de cualquier categoría Bool. Dado que\(\mathbb{B}\) = {false, true}, la Definición 2.46 dice que una categoría Bool consta de dos cosas:

(i) un conjunto Ob (X), y

(ii) por cada x, y\(\in\) Ob (X) un elemento X (x, y)\(\in\) B, es decir, ya sea X (x, y) = verdadero o X (x, y) = falso.

Usaremos estas dos cosas para comenzar a formar un preorden cuyos elementos son los objetos de X. Así que llamemos al preorden (X, ≤), y vamos X = Ob (X). Para la relación ≤, declaremos x ≤ y iff X (x, y) = true. Tenemos los componentes de un preorden, pero para que funcione, la relación ≤ debe ser reflexiva y transitiva. Veamos si las obtenemos de las propiedades garantizadas por la Definición 2.46:

(a) para cada elemento x\(\in\) X tenemos true ≤ X (x, x),

(b) por cada tres elementos x, y, z\(\in\) X tenemos X (x, y)\(\wedge\) X (y, z) ≤ X (x, z).
Para b\(\in\) Bool, si true ≤ b entonces b = true, entonces la primera sentencia dice X (x, x) = true, que significa x ≤ x. Para el segundo enunciado, se puede consultar la Ec. (2.28). Dado que false ≤ b para todos b\(\in\) B, la única forma en que la declaración (b) tiene alguna fuerza es si X (x, y) = true y X (y, z) = true, en cuyo caso fuerza X (x, z) = true. Esta condición se traduce exactamente como decir que x ≤ y e y ≤ z implica x ≤ z. Así, hemos obtenido reflexividad y transitividad de los dos axiomas de las categorías Bool.

En el Ejemplo 2.47, construimos una categoría Bool a partir de una preorden. Dejamos al lector generalizar este ejemplo y mostrar que las dos construcciones son inversas; ver Ejercicio 2.50.

Ejemplo 2.50.

1. Comienza con un preorden (P, ≤), y utilízalo para definir una categoría Bool como hicimos en el Ejemplo 2.47. En la prueba del Teorema 2.49 mostramos cómo convertir esa categoría Bool nuevamente en un preorden. Demuestra que al hacerlo, obtienes el preorder con el que empezaste.
2. Del mismo modo, demuestre que si convierte una categoría Bool en una preorden usando la prueba anterior, y luego vuelve a convertir la preorden en una categoría Bool usando su método, obtiene la categoría Bool con la que comenzó. ♦

Ahora discutimos una hermosa aplicación de la noción de categorías enriquecidas: espacios métricos.

Espacios métricos Lawvere

Los espacios métricos ofrecen una manera precisa de describir espacios de puntos, cada par de los cuales está separado por cierta distancia. Aquí está la definición habitual:

Definición: 2.51.

Un espacio métrico (X, d) consta de:

(i) un conjunto X, cuyos elementos se denominan puntos, y

(ii) una función d: X × X →\(\mathbb{R}\)\(_≥0\), donde d (x, y) se llama la distancia entre x e y

Estos componentes deben satisfacer cuatro propiedades:

(a) por cada x\(\in\) X, tenemos d (x, x) = 0,
(b) por cada x, y\(\in\) X, si d (x, y) = 0 entonces x = y,

(c) por cada x, y\(\in\) X, tenemos d (x, y) = d (y, x), y
(d) por cada x, y, z\(\in\) X, tenemos d (x, y) + d (y, z) ≥ d (x, z).

La cuarta propiedad se llama la desigualdad triangular.
Si pedimos en cambio en (ii) una función d: X × X → [0, ∞] =\(\mathbb{R}\)\(_{≥0}\)\(\cup\) {∞}, llamamos a (X, d) un espacio métrico extendido.

La desigualdad triangular dice que al trazar una ruta de x a z, la distancia es siempre como máximo lo que obtienes eligiendo un punto intermedio y e yendo

x → y → z.

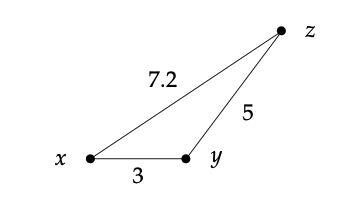
Se puede invocar de tres formas diferentes en la imagen anterior: 3 + 5 ≥ 7.2, pero también 5 + 7.2 ≥ 3 y 3 + 7.2 ≥ 5. Ah sí, y 5 + 3 ≥ 7.2, 7.2 + 5 ≥ 3 y 7.2 + 3 ≥ 5.

La desigualdad triangular captura maravillosamente algo sobre la distancia, al igual que el hecho de que d (x, x) = 0 para cualquier x. No obstante, las otras dos condiciones no son tan generales como nos gustaría. En efecto, hay muchos ejemplos de cosas que “deberían” ser espacios métricos, pero que no satisfacen las condiciones (b) o (c) de la Definición 2.51.

Por ejemplo, qué pasa si tomamos X para ser lugares en tu barrio, pero en vez de medir la distancia, quieres que d (x, y) mida el esfuerzo para llegar de x a y. Entonces si hay alguna colina, el axioma de simetría, d (x, y) =\(^{?}\) d (y, x), falla: es más fácil pasar de x cuesta abajo a y luego ir de y cuesta arriba a x.

Otra forma de encontrar un modelo que rompa el axioma de simetría es imaginar que los elementos de X no son puntos, sino regiones enteras como EEUU, España y Boston. Digamos que la distancia de la región A a la región B se entiende usando la configuración “Te pondré en una parte arbitraria de A y solo tienes que llegar a cualquier parte de B; ¿cuál es la distancia en el peor de los casos?” Entonces d (EU, España) es la distancia desde algún lugar del oeste de EU hasta el extremo occidental de España: solo tienes que meterte en España, pero empiezas en la peor parte posible de EU por hacerlo.

Ejemplo 2.52.

¿Qué distancia es mayor bajo la descripción anterior, d (España, US) o d (US, España)? ♦

Esta noción de distancia, que está fuertemente relacionada con algo llamado distancia de Hausdorff,\(^{3}\) volverá a satisfacer la desigualdad triangular, pero viola la condición de simetría. También viola otra condición, porque d (Boston, EU) = 0. No importa dónde se encuentre en Boston, la distancia al punto más cercano de EU es 0. Por otro lado, d (EU, Boston)\(\neq\) 0.

Por último, se puede imaginar un uso para distancias que no son finitas. En cuanto a mi esfuerzo, la distancia de aquí a Plutón es ∞, y no sería mejor que Plutón siguiera siendo un planeta. De manera similar, en términos de distancia de Hausdorff, discutida anteriormente, la distancia entre dos regiones suele ser infinita, por ejemplo, la distancia entre {r\(\in\)\(\mathbb{R}\) | r < 0} y {0} como subconjuntos de (\(\mathbb{R}\), d) es infinita.

Cuando bajamos las condiciones (b) y (c) y permitimos distancias infinitas, obtenemos la noción relajada de espacio métrico, propuesta por primera vez por Lawvere. Recordemos el preorden monoidal simétrico Costo = ([0, ∞], ≥, 0, +) del Ejemplo 2.37.

Definición: 2.53.

Un espacio métrico Lawvere es una categoría Costo.

Esta es una definición muy compacta, pero tiene un puñetazo. Vamos a averiguar lo que significa,

relacionándolo con la definición habitual de espacio métrico. Por Definición 2.46, a Costo-categoría X consiste en:

(i) un conjunto Ob (X),
(ii) por cada x, y\(\in\) Ob (X) un elemento X (x, y)\(\in\) [0, ∞].

Aquí el conjunto Ob (X) está jugando el papel del conjunto de puntos, y X (x, y)\(\in\) [0, ∞] está jugando el papel de distancia, así que escribamos un pequeño traductor:

X: = Ob (X) d (x, y) := X (x, y).

Las propiedades de una categoría enriquecida en Costo son: (a) 0 ≥ d (x, x) para todos \(\in\)x X, y
(b) d (x, y) + d (y, z) ≥ d (x, z) para todos x, y, z\(\in\) X.

Desde d (x, x)\(\in\) [0, ∞], si 0 ≥ d (x, x) entonces d (x, x) = 0. Entonces la primera condición es equivalente a la primera condición de la Definición 2.51, es decir, d (x, x) = 0. La segunda condición es la desigualdad triangular.

Ejemplo 2.54.

Al conjunto\(\mathbb{R}\) de números reales se le puede dar una estructura espacial métrica y, por lo tanto, una estructura espacial métrica Lawvere. A saber, d (x, y) := | y − x |, el valor absoluto de la diferencia. Entonces d (3, 7) = 4.

Ejercicio 2.55.

Considera el preorden monoidal simétrico (\(\mathbb{R}_{≥0}\), ≥, 0, +), que es casi lo mismo que Costo, excepto que no incluye ∞. ¿Cómo caracterizarías la diferencia entre un espacio métrico Lawvere y una categoría (\(\mathbb{R}_{≥0}\), ≥, 0, +) en el sentido de la Definición 2.46? ♦

Presentación de espacios métricos con gráficos ponderados Así como uno puede convertir un diagrama de Hasse en un preorden, se puede convertir cualquier gráfico ponderado un gráfico cuyos bordes estén etiquetados con números w ≥ 0 en un espacio métrico Lawvere. De hecho, las consideraremos como gráficas etiquetadas con elementos de [0, ∞], y más precisamente las denominaremos gráficas ponderadas por costos. \(^{4}\)

Uno podría pensar en un gráfico ponderado por costos como describir una ciudad con algunas carreteras de un solo sentido (una carretera de ida se modela como dos carreteras de un solo sentido), cada una con algún esfuerzo para atravesar, que por simplicidad solo llamamos longitud. Por ejemplo, considere los siguientes gráficos ponderados:

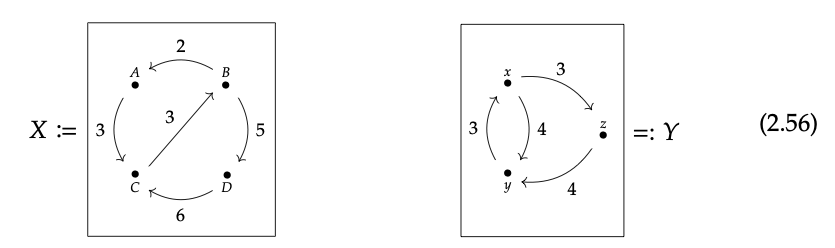
Dada una gráfica ponderada, se forma una métrica\(d_{X}\) en su conjunto X de vértices estableciendo d (p, q) para que sea la longitud del camino más corto de p a q. Por ejemplo, aquí está la tabla de distancias para Y

Ejercicio 2.58.

Rellene la siguiente tabla de distancias en la gráfica ponderada X de la Ec. (2.56)

Arriba convertimos una gráfica ponderada G, por ejemplo como se muestra en la Ec. (2.56), en una tabla de distancias, pero esto requiere un poco de pensamiento. Hay una construcción más directa para tomar G y obtener una matriz cuadrada M G, cuyas filas y columnas están indexadas por los vértices de G. Para hacerlo, establezca M G en 0 a lo largo de la diagonal, que sea ∞ donde falte un borde y que sea el peso del borde si hay un borde.

Por ejemplo, la matriz asociada a Y en la Ec. (2.56) sería

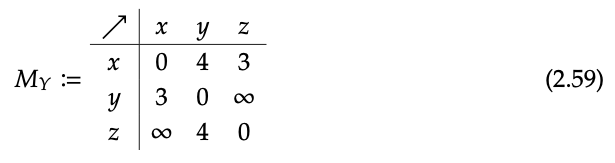
En cuanto veas cómo hicimos esto, entenderás que no hace falta pensar en convertir una gráfica ponderada G en una matriz M G de esta manera. Veremos más adelante en la Sección 2.5.3 que las “matrices de distancia” más difíciles d Y, como la Ec. (2.57), se pueden obtener de las matrices gráficas fáciles M Y, como la Ec. (2.59), repitiendo cierto tipo de “multiplicación matricial”.

Ejercicio 2.60.

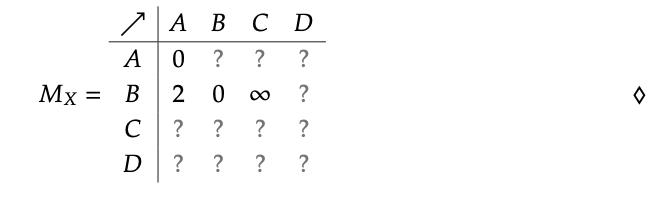
Rellene la matriz M X asociada a la gráfica X en la Ec. (2.56):

V -variaciones en preordenes y espacios métricos

Hemos contado la historia de Bool y Cost. Pero en la Sección 2.2.4 dimos ejemplos de muchos otros preordenes monoidales, y cada uno sirve como base de enriquecimiento para una especie de categoría enriquecida. ¿Cuáles de ellos son útiles? Algo sólo se vuelve útil cuando alguien encuentra un uso para ello. Encontraremos usos para algunos y no para otros, aunque animamos a los lectores a pensar en lo que significaría enriquecer en las diversas categorías monoidales discutidas anteriormente; tal vez puedan encontrar un uso que no hemos explorado.

Ejercicio 2.61.

Recordemos el preorden monoidal NMY: = (P, ≤, sí, min) del Ejercicio 2.34. Interpretar qué es una categoría NMY ♦

siguientes dos ejercicios, utilizamos gráficas ponderadas en V para construir categorías V. Esto es posible porque usaremos preordenes que, como Bool y Cost, tengan uniones.

Ejercicio 2.62.

Sea M un conjunto y que M: = (P (M),\(\subseteq\), M,\(\cap\)) sea el preorden monoidal cuyos elementos son subconjuntos de M.

Alguien da la siguiente interpretación, “para cualquier conjunto M, imagínelo como el conjunto de modos de transporte (por ejemplo, automóvil, barco, pie). Entonces una categoría M X te dice todos los modos que te llevarán de a todo el camino a b, para dos puntos cualquiera a, b\(\in\) Ob (X)”.

1. Dibuja una gráfica con cuatro vértices y cuatro o cinco aristas, cada una etiquetada con un subconjunto de M = {carro, bote, pie}.
2. A partir de esta gráfica es posible construir una categoría M, donde el hom-objeto de x a y se calcula de la siguiente manera: para cada ruta p de x a y, tomar la intersección de los conjuntos etiquetando los bordes en p. Entonces, tomar la unión de los estos conjuntos sobre todos los caminos p de x a y. Escriba la matriz correspondiente de cuatro por cuatro de hom-objects, y convencerse de que de hecho se trata de una categoría M.
3. ¿La interpretación de la persona se ve bien, o se equivoca sutilmente de alguna manera? ♦

Ejercicio 2.63.

Considere el preorden monoidal W: = (\(\mathbb{N}\)\(\cup\){∞}, ≤, ∞, min).

1. Dibuja una pequeña gráfica etiquetada por elementos de N\(\cup\) {∞}.
2. Escriba la matriz cuyas filas y columnas están indexadas por los nodos en el
3. gráfico, y cuya entrada (x, y) th está dada por el máximo en todas las rutas p de x
4. a y de la etiqueta de borde mínima en p.
5. Demostrar que esta matriz es la matriz de hom-objetos para una categoría W. Esta voluntad
6. te dan una idea de cómo funciona W.
7. Informar una interpretación, así en el Ejercicio 2.62, de cómo imaginar el enriquecimiento en W. ♦