2.4: Construcciones en categorías V

Última actualización
Guardar como PDF

Page ID: 112327

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ahora que tenemos una buena intuición para lo que son las categorías V, damos tres ejemplos de lo que se puede hacer con las categorías V. El primero (Sección 2.4.1) se conoce como cambio de base. Esto nos permite utilizar una f monótona monoidal: V → W para construir categorías W a partir de categorías V. La segunda construcción (Sección 2.4.2), la de los funtores V, nos permite completar la analogía: un preorden es a una categoría Bool como un mapa monótono es a qué? La tercera construcción (Sección 2.4.2) se conoce como un V-producto, y nos da una manera de combinar dos categorías V.

Cambio de la base del enriquecimiento

Cualquier V → W monótona monoidal entre preordenes monoidales simétricos nos permite convertir categorías V en categorías W.
Construcción 2.64. Sea f: V → W un monótona monoidal. Dada una categoría V C, uno forma la categoría W asociada, digamos de la$C_{f}$ siguiente manera.

(i) Tomamos los mismos objetos: Ob ($C_{f}$) := Ob (C).

(ii) Para cualquier c, d$\in$ Ob (C), poner$C_{f}$ (c, d) := f (C (c, d)).

Esta construcción$C_{f}$ efectivamente obedece a la definición de categoría W, como puede verse aplicando la Definición 2.41 (de monótona monoidal) y la Definición 2.46 (de categoría V):

(a) por cada $\in$c C, tenemos

$I_{W}$≤ f ($I_{V}$) (f es monótona monoidal)

≤ f (C (c, c)) (C es categoría V)

=$C_{f}$ (c, c) (definición de$C_{f}$)

(b) por cada c, d, e$\in$ Ob (C) tenemos

$C_{f}$c, d)$⊗_{W}$$C_{f}$ (d, e) = f (C (c, d))$⊗_{W}$ f (C (d, e)) (definición de$C_{f}$)

≤ f (C (c, d)$⊗_{V}$ C (d, e)) (f es monótona monoidal)

≤ f (C (c, e)) (C es categoría V)

=$C_{f}$ (c, e) (definición de$C_{f}$)

Ejemplo 2.65.

Como ejemplo, considere la función f: [0, ∞] → {true, false} dada por

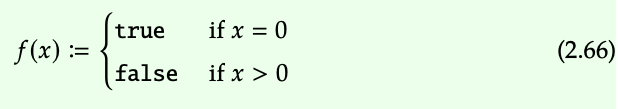
$Screen Shot 2021-01-11 a las 2.20.53 AM.png$

Es fácil comprobar que f es monótona y que f conserva el producto monoidal y la unidad monoidal; es decir, es fácil demostrar que f es un monótono monoidal. (Recordar Ejercicio 2.44.)

Así f nos permite convertir espacios métricos de Lawvere en preordenes.

Ejercicio 2.67.

Recordemos las “regiones del mundo” Lawvere espacio métrico del Ejercicio 2.52 y el texto sobre él. Acabamos de aprender que, usando la f monótona monoidal en la Ec. (2.66), podemos convertirla en un preorden. Dibuja el diagrama de Hasse para el preorden correspondiente a las regiones: Estados Unidos, España y Boston. ¿Cómo podría interpretar esta relación de preorden? ♦

Ejercicio 2.68.

Encuentra otro monoidal monótona g: Costo → Bool diferente al definido en la Ec. (2.66).
Usando Construcción 2.64, tanto tu monótona g monoidal como la monótona f monoidal en la Ec. (2.66) se pueden usar para convertir un espacio métrico Lawvere en un preorden. Encuentra un espacio métrico Lawvere X en el que dan diferentes respuestas,$X_{f}$$\neq$$X_{g}$. ♦

Functores enriquecidos

La noción de funtor proporciona el tipo más importante de relación entre categorías.

Definición: 2.69.

Deja que X e Y sean categorías V. Un V-functor de X a Y, denotado F: X → Y, consiste en un constituyente:

(i) una función F: Ob (X) → Ob (Y)

sujeto a una restricción

(a) para todos x 1, x 2$\in$ Ob (X), uno tiene X ($x_{1}$,$x_{2}$) ≤ Y (F ($x_{1}$), F ($x_{2}$)).

Ejemplo 2.70.

Por ejemplo, hemos dicho varias veces —por ejemplo en el Teorema 2.49—que los pedidos anticipados son categorías Bool, donde X ($x_{1}$,$x_{2}$) = true se denota$x_{1}$ ≤ $x_{2}$. Uno esperaría que los mapas monótona entre preordenes correspondan exactamente a Bool -functors, y eso es cierto. Un mapa monótono (X,$≤_{X}$) → (Y,$≤_{Y}$) es una función F: X → Y tal que para cada$x_{1}$,$x_{2}$$\in$ X, si$x_{1}$ ≤$_{X}$ x2 entonces F ($x_{1}$)$≤_{Y}$ F ($x_{2}$). En otras palabras, tenemos

X ($x_{1}$,$x_{2}$) ≤ Y (F ($x_{1}$), F ($x_{2}$)),

donde el ≤ anterior se lleva a cabo en la categoría enriquecedora V = Bool; esta es exactamente la condición de la Definición 2.69.

OBSERVACIÓN 2.71. De hecho, tenemos lo que se llama una equivalencia de categorías entre la categoría de preordenes y la categoría de Bool -categorías. En el siguiente capítulo desarrollaremos las ideas necesarias para exponer lo que esto significa precisamente (Comentario 3.59).

Ejemplo 2.72.

Los espacios métricos Lawvere son categorías de costos. Es de esperar que la definición de Cost -functor devuelva una buena noción —un “amigo” —de la teoría de los espacios métricos, y lo hace: recupera la noción de función Lipschitz. Una función Lipschitz (o más precisamente, 1-Lipschitz) es aquella bajo la cual la distancia entre cualquier par de puntos no aumenta. Es decir, dados los espacios métricos de Lawvere (X,$d_{X}$) e (Y,$d_{Y}$), un Cost - functor entre ellos es una función F: X → Y tal que para cada$x_{1}$,$x_{2}$$\in$ X tenemos$d_{X}$ ($x_{1}$,$x_{2}$) ≥$d_{Y}$ (F ($x_{1}$), F ($x_{2}$)).

Ejercicio 2.73.

Los conceptos de opuesto, daga y esqueleto (ver Ejemplos 1.58 y 1.72 y Remark 1.35) se extienden desde los pedidos anticipados hasta las categorías V. Lo opuesto de una categoría V X se denota$X^{op}$ y se define por

(i) Ob ($X^{op}$) := Ob (X), y
(ii) para todos x, y$\in$ X, tenemos$X^{op}$ (x, y) := X (y, x).

Una categoría V X es una daga categoría V si la función de identidad es un funtor V †: X →$X^{op}$. Y una categoría V esquelética es aquella en la que si I ≤ X (x, y) y I ≤ X (y, x), entonces x = y.

Recordemos que un espacio métrico extendido (X, d) es un espacio métrico Lawvere con dos propiedades adicionales; vea las propiedades (b) y (c) en la Definición 2.51.

1. Mostrar que una daga esquelética Costo -categoría es un espacio métrico extendido.
2. Utilice el Ejercicio 1.73 para dar sentido a la siguiente analogía: “los pedidos anticipados son para conjuntos como los espacios métricos de Lawvere son a espacios métricos extendidos”.

Producto V -categorías

Si V = (V, ≤, I,) es un preorden monoidal simétrico y X e Y son categorías V, entonces podemos definir su V-producto, que es una nueva categoría V.

Definición: 2.74.

Deja que X e Y sean categorías V. Definir su producto V, o simplemente producto, para que sea la categoría V X × Y con

(i) Ob (X × Y) := Ob (X) × Ob
(Y), (ii) (X × Y) ((x, y), (x ′, y ′)) := X (x, x ′) Y (y, y ′),

para dos objetos (x, y) y (x ′, y ′) en Ob (X × Y).

Las categorías V del producto son, de hecho, categorías V (Definición 2.46); ver Ejercicio 2.75.

Ejercicio 2.75.

Que X × Y sea el V-producto de las categorías V como en la Definición 2.74.

Comprobar que para cada objeto (x, y)$\in$ Ob (X × Y) tenemos I ≤ (X × Y) ((x, y), (x, y)).
Verifica que por cada tres objetos ($x_{1}$,$y_{1}$$y_{2}$)$x_{2}$, (,) y ($x_{3}$,$y_{3}$), tenemos (X×Y) (($x_{1}$,$y_{1}$)$x_{2}$, (,$y_{2}$)) (X×Y) (($x_{2}$,$y_{2}$)$x_{3}$, (,$y_{3}$) ≤ (X×Y) (($x_{1}$,$y_{1}$)$x_{3}$, $y_{3}$)).
Dijimos al inicio de la Sección 2.3.1 que aquí se requeriría la simetría de V (condición d) de la Definición 2.2). Señale exactamente dónde se usa esa condición. ♦

Al tomar el producto de dos preordenes (P,$≤_{P}$) × (Q,$≤_{Q}$), como se describe por primera vez en el Ejemplo1.56$p_{1}$, wesaythat ($p_{2}$,$q_{1}$$q_{2}$) ≤ (,) iff ambos$p_{1}$$q_{1}$ ≤$p_{2}$ Y ≤$q_{2}$; el AND es el producto monoidal de Bool. Así, el producto de los pedidos anticipados es un ejemplo de un producto Bool.

Ejemplo 2.76.

Sea X e Y los espacios métricos de Lawvere (es decir, categorías de costos) definidos por las siguientes gráficas ponderadas:

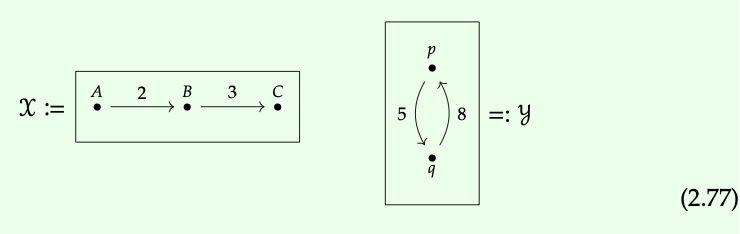
$Screen Shot 2021-01-11 a las 12.06.31 PM.png$

Su producto se define tomando el producto de sus conjuntos de objetos, por lo que hay seis objetos en X × Y. Y la distancia$d_{X × Y}$ ((x, y), (x ′, y ′)) entre dos puntos cualesquiera viene dada por la suma d X (x, x ′) + d Y (y, y ′).

Examine la siguiente gráfica y asegúrese de comprender lo fácil que es derivar de las gráficas ponderadas para X e Y en la Ec. (2.77):

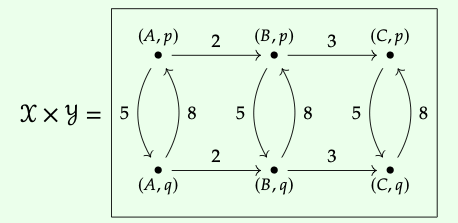
$Screen Shot 2021-01-11 a las 12.08.11 PM.png$

Ejercicio 2.78.

Considerar$\mathbb{R}$ como un espacio métrico Lawvere, es decir, como una categoría Costo (ver Ejemplo 2.54). Formar el Costo -producto$\mathbb{R}$ ×$\mathbb{R}$. ¿Cuál es la distancia de (5, 6) a (−1, 4)?

Pista: aplicar Definición 2.74; la respuesta no es$\sqrt{40}$. ♦

En términos de matrices, los productos V también son bastante sencillos. Generalizan lo que se conoce como el producto Kronecker de matrices. Las matrices para X e Y en la Ec. (2.77) se muestran a continuación

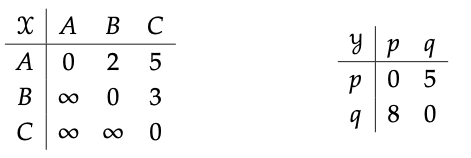
$Screen Shot 2021-01-11 a las 12.12.05 PM.png$

y su producto es el siguiente:

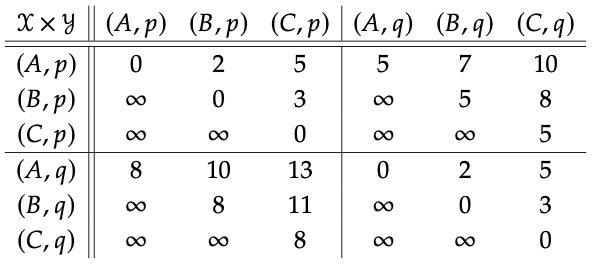
$Screen Shot 2021-01-11 a las 12.12.44 PM.png$

Hemos dibujado la matriz del producto como una matriz de bloques, donde hay un bloque con forma de X por cada entrada de Y. Asegúrese de que puede ver cada bloque como la matriz X desplazada por una entrada en Y. Esto viene directamente de la fórmula de la Definición 2.74 y el hecho de que el producto monoidal en Costo es +.