2.5: Computación presentó categorías V con matriz mult

Última actualización
Guardar como PDF

Page ID: 112320

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la Sección 2.3.3 prometimos una forma sencilla de construir la representación matricial de una categoría Costo a partir de una gráfica ponderada por costos. Para ello, utilizamos una multiplicación matricial generalizada. Demostraremos que esto funciona, no sólo para Cost, sino también para Bool, y muchos otros preordenes monoidales. El bien requerido del preorden es el de ser un quantale unital, conmutativo. Se trata de preordenes con todas las uniones, más un ingrediente adicional, siendo monoidal cerrado, que definimos a continuación, en la Sección 2.5.1. La definición de quantale se dará en la Sección 2.5.2

Preordenes cerrados monoidales

La definición de categoría V tiene sentido para cualquier preorden monoidal simétrico V. Pero eso no significa que cualquier base de enriquecimiento V sea tan útil como cualquier otra. En esta sección definimos categorías monoidales cerradas, ¡que en particular se enriquecen! “Antes de que realmente puedas enriquecer a los demás, realmente deberías enriquecerte a ti mismo”.

Definición: Word

Un preorden monoidal simétrico V = (V, ≤, I,) se llama simétrico monoidal cerrado (o simplemente cerrado) si, por cada dos elementos v, w$\in$ V, hay un elemento v = w en V, llamado el hom-elemento, con la propiedad

(a v) ≤ w iff a ≤ (v −o w) . (2.80)

para todos a, v, w$\in$ V.

Observación 2.81. El término 'cerrado' se refiere al hecho de que un hom-elemento puede construirse para dos elementos cualesquiera, por lo que el preorden puede verse como cerrado bajo la operación de “tomar homs”. En capítulos posteriores conoceremos los conceptos estrechamente relacionados de categorías cerradas compactas (Definición 4.58) y categorías cerradas cartesianas (Sección 7.2.1) que hacen que esta idea sea más precisa. Ver especialmente Ejercicio 7.11.

Uno puede considerar el elemento hom-element v −o w como una especie de “convertidor v -a-w de un solo uso”. Entonces la Eq. (2.80) dice que a y v son suficientes para obtener w si y solo si a es suficiente para obtener un convertidor v -to- w de un solo uso.

Ejercicio 2.82.

Condición Eq. (2.80) dice precisamente que existe una conexión Galois en el sentido de la Definición 1.95. Demostremos este hecho. En particular, probaremos que un preorden monoidal es monoidal cerrado iff, dado cualquier $\in$v V, el mapa (− v): V → V dado multiplicando por v tiene un derecho adjunto. Escribimos este derecho adjunto (v −o−): V → V.

Usando la Definición 2.2, mostrar que (− v) es monótona.
Suponiendo que V está cerrado, mostrar que para todos v, w$\in$ V tenemos ((v −o w) v) ≤ w.
Usando 2., mostrar que (v −o−) es monótona.
Concluir que un preorden monoidal simétrico se cierra si y solo si el mapa monótona (− v) tiene un derecho contiguo. ♦

Ejemplo 2.83.

El preorden monoidal Costo = ([0, ∞], ≥, 0, +) es monoidal cerrado. De hecho, para cualquier x, y$\in$ [0, ∞], defina x −o y: = max (0, y − x). Entonces, para cualquier a, x, y$\in$ [0, ∞], tenemos

a + x ≥ y iff a ≥ y − x iff max (0, a) ≥ max (0, y − x) iff a ≥ (x −o y)

por lo que −o satisface la condición de la Ec. (2.80).
Tenga en cuenta que antes no hemos considerado la resta en Costo; ¡de hecho podemos usar el cierre monoidal para definir la resta en términos del orden y la estructura monoidal!

Ejercicio 2.84.

Mostrar que Bool = ($\mathbb{B}$, ≤, true,$\land$) es monoidal cerrado. ♦

Ejemplo 2.85.

Un no-ejemplo es ($\mathbb{B}$, ≤, false,$\lor$). En efecto, supongamos que tenemos un operador −o como en la Definición 2.79. Obsérvese que false ≤ p −o q, para cualquier p, q no importa lo que −o sea, porque false es menor que todo. Pero usando a = false, p = true, y q = false, entonces obtenemos una contradicción: (a ‖ p)$\nleq$ q y sin embargo a ≤ (p −o q).

Ejemplo 2.86.

Empezamos este capítulo hablando de teorías de recursos. ¿Cómo se ve la estructura cerrada desde esa perspectiva? Por ejemplo, en química diría que por cada dos colecciones de materiales c, d se puede formar una colección de material c −o d con la propiedad que para cualquier a, se tiene

a + c → d si y solo si a → (c −o d).

O más abajo a la tierra, ya que tenemos la reacción 2$H_{2}$ O + 2Na → 2NaOH +$H_{2}$, también debemos tener

2$H_{2}$ O → (2Na −o (2NaOH +$H_{2}$))

Entonces, a partir de solo dos moléculas de agua, se puede formar una cierta sustancia, y no muchas

las sustancias se ajustan a la factura: nuestro tapete de preventa de materiales químicos no está cerrado.

Pero no es tan descabellado: esta nueva sustancia hipotética (2Na −o (2NaOH +$H_{2}$)) no es realmente una sustancia, sino una reacción potencial: es decir, la de convertir un sodio en sodio-hidróxido-más-hidrógeno. Dos moléculas de agua desbloquean ese potencial.

Proposición 2.87.

Supongamos que V = (V, ≤, I,, −o) es un preorden monoidal simétrico que está cerrado. Entonces

(a) Por cada v$\in$ V, el mapa monótona − v: (V, ≤) → (V, ≤) se deja adjunto a v −o −: (V, ≤) → (V, ≤).

(b) Para cualquier elemento v$\in$ V y conjunto de elementos A$\subseteq$ V, si existe la unión a$\bigvee$$_{a \in\ A}$ $\in$A a entonces también lo hace $\in$un A v a y tenemos

$\left(v \otimes \bigvee_{a \in A} a\right) \cong \bigvee_{a \in A}(v \otimes a)$(2.88)

(d) Para cualquier v$\in$ V, tenemos v $\cong$(I −o v).

(e) Para cualquier u, v, w$\in$ V, tenemos (u −o v) (v −o w) ≤ (u −o w).

Comprobante. Pasamos por las reclamaciones en orden.

(a) La definición de (− v) que se deja junto a (v −o) es exactamente la condición Eq. (2.80); ver Definición 1.95 y Ejercicio 2.82.

(b) Esto se desprende de (a), utilizando el hecho de que los anexos izquierdos conservan uniones (Proposición 1.111).

(c) Esto se desprende de (a), utilizando la caracterización equivalente de la conexión Galois en la Proposición 1.107. Más concretamente, a partir de la reflexividad (v −o w) ≤ (v −o w), obtenemos (v −o w) v ≤ w Eq. (2.80), y estamos hechos por simetría, que dice v (v −o w) = ( v −o w) v.

(d) Dado que v I = v ≤ v, la Eq. (2.80) dice v ≤ (I −o v). Para la otra dirección, tenemos (I −o v) = I (I −o v) ≤ v by (c).

(e) Para obtener esta desigualdad, solo necesitamos u (u −o v) (v −o w) ≤ w. Pero esto sigue por dos aplicaciones de c) . □

Uno podría leer (c) diciendo “si tengo un v y un convertidor v -to- w de un solo uso, puedo tener un w”. Uno podría leer (d) diciendo “tener una v es lo mismo que tener un convertidor de nada a v de un solo uso”. Y uno podría leer (e) como diciendo “si tengo un convertidor u -a-v de un solo uso y un convertidor v -to- w de un solo uso, puedo obtener un convertidor u -to- w de un solo uso.

Observación 2.89. Podemos considerar que V se enriquece en sí mismo. Es decir, por cada v, w$\in$ Ob (V), podemos definir V (v, w) := (v −o w)$\in$ V. Para que esto sea realmente un enriquecimiento, solo necesitamos verificar las dos condiciones de la Definición 2.46. La primera condición I ≤ X (x, x) = (x −o x) se satisface porque I x ≤ x. La segunda condición es satisfecha por la Proposición 2.87 (e).

Quantales

Para realizar la multiplicación matricial sobre un preorden monoidal, necesitamos una cosa más: las uniones. Éstas se definieron primero en la Definición 1.81.

Definición: 2.90.

Un quantale conmutativo unital es un preorden cerrado monoidal simétrico V = (V, ≤, I,, −o) que tiene todas las uniones:$\bigvee$ A existe para cada$\bigvee$ A $\subseteq$V. En particular, a menudo denotamos la unión vacía por 0: =$\bigvee$ Ø.

Siempre que hablamos de quantales en este libro, nos referimos a quantales conmutativos unitales. Intentaremos recordarle eso al lector. También hay aplicaciones muy interesantes de los quantales no conmutativos; ver Sección 2.6.

Ejemplo 2.91.

En el Ejemplo 2.83, vimos que Costo es monoidal cerrado. Para verificar si el costo es una cantidad, tomamos un conjunto arbitrario de elementos A$\subseteq$ [0, ∞] y preguntamos si tiene$\bigvee$ una unión A. Para ser un join, necesita satisfacer dos propiedades:

a. a ≥$\bigvee$ A para todas las a$\in$ A, y

b. si b$\in$ [0, ∞] es cualquier elemento tal que a ≥ b para todos a$\in$ A, entonces$\bigvee$ A ≥ b. De hecho podemos definir tal unión: normalmente se le llama el infimum, o mayor límite inferior, de A. $^{5}$Por ejemplo, si A = {2, 3} entonces$\bigvee$ A = 2. También tenemos uniones para conjuntos infinitos: si B = {2.5, 2.05, 2.005,.}, su infimum es 2. Por último, para decir que ([0, ∞], ≥) tiene todas las uniones, necesitamos que exista una unión para el conjunto vacío A = Ø también. La primera condición se vuelve vacua no hay a's en A pero la segunda condición dice que para cualquier b$\in$ [0, ∞] tenemos$\bigvee$ Ø ≥ b; esto significa$\bigvee$ Ø = ∞.

Así, efectivamente ([0, ∞], ≥) tiene todas las uniones, por lo que el Costo es una cuantale.

Ejercicio 2.92.

1. Qué es$\bigvee$ Ø, que generalmente denotamos 0, en el caso

a. V = Bool = ($\mathbb{B}$, ≤, true,$\wedge$)?

b. v = Costo = ([0, ∞], ≥, 0, +)?

2. Cuál es el join x$\lor$ y en el caso

a. V = Bool, y x, y$\in$$\mathbb{B}$ ¿son booleanos?

b. V = Costo, y x, y$\in$ [0, ∞] son distancias? ♦

Ejercicio 2.93.

Mostrar que Bool = ($\mathbb{B}$, ≤, true,$\wedge$) es una quantale. ♦

Ejercicio 2.94.

Sea S un conjunto y recuerde el preorden monoidal del conjunto de potencia (P (S)$\subseteq$, S,$\land$) del Ejercicio 2.35. ¿Es un quantale? ♦

Observación 2.95. Se puede personificar la noción de quantale unital, conmutativa como una especie de navegante. Un navegante es alguien que entiende “llegar de un lugar a otro”. A los diferentes navegantes se les pueden preocupar o entender diferentes aspectos, ya sea que uno pueda pasar de A a B, cuánto tiempo llevará, qué modos de viaje funcionarán, etc. pero ciertamente tienen algunos puntos en común. Lo más importante es que un navegante necesita poder leer un mapa: dadas las rutas A a B y B a C, entienden cómo obtener una ruta A a C. Y saben buscar sobre el espacio de waypoints para llegar de la A a la C. Estos corresponderán al producto monoidal y a las operaciones de unión, respectivamente.

Proposición 2.96.

Sea P = (P, ≤) un preorden. Tiene todas las uniones iff tiene todo cumple.

Comprobante. Las uniones (resp. meets) en P son las meets (resp. joins) en$P^{op}$, por lo que las dos afirmaciones son duales: basta con mostrar que si P tiene todas las uniones entonces tiene todas las juntas.

Supongamos que P tiene todas las uniones y supongamos que A$\subseteq$ P es un subconjunto para el que queremos themeet. Considera el conjunto$M_{A}$ := {$\in$p P | p ≤ a para todos a $\in$A} de elementos debajo de todo en A. Sea$m_{A}$ :=$\bigvee$$_{p \in\ M}$$_{A}$ p su unión. Afirmamos que$M_{A}$ es un encuentro para A. Primero necesitamos saber que para cualquier a $\in$A tenemos$m_{A}$ ≤ a, pero esto es por definición de join: ya que todos p$\in$$M_{A}$ satisfacen p ≤ a, también lo hace su unión$m_{A}$ ≤ a. Segundo necesitamos saber que para cualquier m ′$\in$ P con m ′ ≤ a para todos a $\in$A, tenemos m ′ ≤ m. Pero cada uno de esos m ′ es en realidad un elemento de$M_{A}$ y m es su unión, así que m ′ ≤ m. Esto completa la prueba. □

En particular, una quantale tiene todas las juntas y todas las uniones, aunque solo la definimos para que tenga todas las uniones.

Observación 2.97. La noción de distancia de Hausdorff puede generalizarse, permitiendo que el papel de Costo sea tomado por cualquier cuantale V. Si X es una categoría V con objetos X, y U\ (\ subseteq\) X y V (\ subseteq\) X, podemos generalizar lo habitual Distancia Hausdorff, a la izquierda abajo, a la fórmula de la derecha:

\ (\ begin {ecuación}
d (U, V) :=\ sup _ {u\ en U}\ inf _ {v\ en V} d (u, v)\ quad x (U, V) :=\ bigwedge_ {u\ en U}\ bigvee_ {v\ in V} X (u, v)
\ end {ecuación}\)

Por ejemplo, si V = Bool, la distancia de Hausdorff entre los sub-preordenes U y V responde a la pregunta “puedo entrar en V desde cada u$\in$ U”, es decir,$\forall{u}$$\in$ U. $\exists{v}$$\in$V. u ≤ v. O para otro ejemplo, utilizar V = P (M) con su interpretación como modos de transporte, como en el Ejercicio 2.62. Entonces la distancia de Hausdorff d (U, V)$\in$ P (M) nos dice esos modos de transporte que nos llevarán a V desde cada punto de la U.

Proposición 2.98.

Supongamos que V = (V, ≤, I,) es cualquier preorden monoidal simétrico que tenga todas las uniones. Entonces V se cierra, es decir, tiene una operación −o y por lo tanto es una quantale si y solo si distribuye sobre uniones; es decir, si la Ec. (2.88) se mantiene para todos los $\in$v V y A$\subseteq$ V.

Comprobante. Mostramos una dirección en la Proposición 2.87 (b): si V es monoidal cerrada entonces se mantiene la Ec. (2.88). Necesitamos demostrar que la Eq. (2.88) sostiene entonces − v: V → V tiene un derecho contiguo v −o−. Esto es sólo el teorema del funtor adjunto, Teorema 1.115. Dice que podemos definir v −o w para ser

$\begin{equation} v −o w:=\bigvee_{\{a \in V \mid a \otimes v \leq w\}} a \end{equation}$□

Multiplicación matricial en un quantale

Un cuantale V = (V, ≤, I,, −o), como se define en la Definición 2.79, proporciona lo necesario para realizar la multiplicación matricial. $^{6}$La fórmula habitual para la multiplicación matricial es:

$\begin{equation} (M * N)(i, k)=\sum_{j} M(i, j) * N(j, k) \end{equation}$. (2.99)

Obtendremos una fórmula donde las uniones representen la operación de suma$\sigma$, y representa la operación del producto ∗. Recordemos nuestra convención de escritura 0: =$\bigvee$.

Definición: 2.100.

Sea V = (V, ≤,, I) una cuantale. Dados los conjuntos X e Y, una matriz con entradas en V, o simplemente una matriz V, es una función M: X × Y → V. Para cualquier x$\in$ X e$\in$ y Y, llamamos M (x, y) la entrada (x, y).

Así es como multiplicas las matrices en V M: X × Y → V y N: Y × Z → V. Su producto se define como la matriz (M ∗ N): X × Z → V, cuyas entradas vienen dadas por la fórmula

$\begin{equation} (M * N)(x, z):=\bigvee_{y \in Y} M(x, y) \otimes N(y, z) \end{equation}$(2.101)

Observe lo similar que es esto a la Ec. (2.99).

Ejemplo 2.102.

Deja que V = Bool. Aquí hay un ejemplo de multiplicación matricial M ∗ N. Aquí X = {1, 2, 3}, Y = {1, 2}, y Z = {1, 2, 3}, las matrices M: X × Y →$\mathbb{B}$ y N: Y × Z → se$\mathbb{B}$ muestran a la izquierda a continuación, y su producto se muestra a la derecha:

$Screen Shot 2021-01-11 a las 4.00.17 PM.png$

La identidad V-matriz en un conjunto X es$I_{X}$: X × X → V dada por

\ (\ begin {ecuación}
I_ {X} (x, y) :=\ left\ {\ begin {array} {ll}
I &\ text {if} x=y\\
0 &\ text {if} x\ neq y
\ end {array}\ right.
\ end {ecuación}\)

Ejercicio 2.103

Anote la matriz de identidad 2×2 para cada uno de los quantales ($\mathbb{N}$, ≤, 1, ∗), Bool = ($mathbb{B}$, ≤, true,$\wedge$) y Cost = ([0, ∞], ≥, 0, +).

Ejercicio 2.104

Sea V = (V, ≤, I,, −o) una cuantale. Utilice la Ec. (2.101) y la Proposición 2.87 para probar lo siguiente.

Demostrar la ley de identidad: para cualquier conjunto X e Y y V -matriz M: X × Y → V, uno tiene I X ∗ M = M.
Demostrar la ley asociativa: para cualquier matriz M: W × X → V, N: X × Y → V, y P: Y × Z → V, una tiene (M ∗ N) ∗ P = M ∗ (N ∗ P) . ♦

Recordemos la gráfica ponderada Y de la Ec. (2.56). Se puede leer la matriz asociada My, y se puede calcular la métrica asociada d Y:

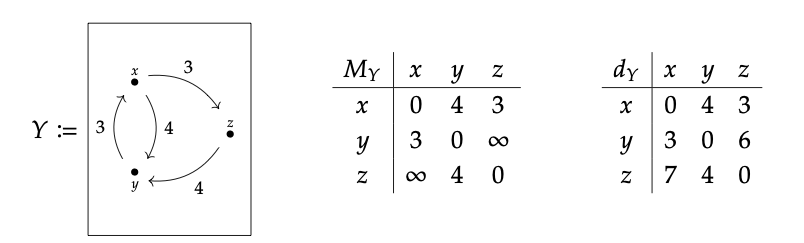
$Screen Shot 2021-01-11 a las 4.15.23 PM.png$

Aquí explicamos completamente cómo calcular d Y usando solo M Y. La matriz M y puede pensarse como que registra la longitud de los caminos que atraviesan los bordes 0 o 1: siendo las diagonales 0 significa que podemos obtener de x a x sin atravesar ningún borde. Cuando podemos llegar de x a y en un borde registramos su longitud en M Y, de lo contrario usamos ∞.

Cuando multiplicamos$M_{Y}$ por sí mismo usando la fórmula Eq. (2.101), el resultado nos$M_{Y}^{2}$ dice la longitud del camino más corto atravesando 2 aristas o menos. Del mismo modo nos$M_{Y}^{3}$ dice sobre el camino más corto que atraviesa 3 bordes o menos:

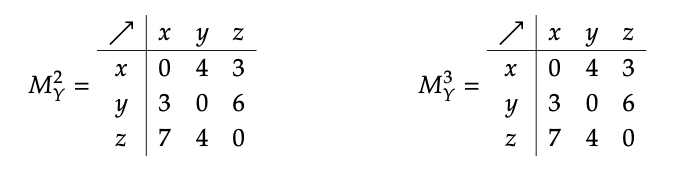
$Screen Shot 2021-01-11 a las 4.19.43 PM.png$

Se ve que los poderes se estabilizan:$M_{Y}^{2}$ =$M_{Y}^{3}$; en cuanto eso sucede uno tiene la matriz de distancias,$d_{Y}$. En efecto,$M_{Y}^{n}$ registra las longitudes del camino más corto atraviesan n bordes o menos, y las potencias siempre se estabilizarán si el conjunto de vértices es finito, ya que el camino más corto de un vértice a otro nunca visitará un vértice dado más de una vez. $^{7}$

Ejercicio 2.105.

Recordemos del Ejercicio 2.60 la matriz$M_{X}$, para X como en la Ec. (2.56). Calcular$M_{X}^{2}$,$M_{X}^{3}$, y$M_{X}^{4}$. Comprueba que eso$M_{X}^{4}$ es lo que obtuviste para la matriz de distancias en el Ejercicio 2.58. ♦

Este procedimiento da un algoritmo para computar la categoría V presentada por cualquier gráfica ponderada en V usando multiplicación matricial.